《Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition》论文阅读之ST-GCN

近日，香港中文大学提出一种时空图卷积网络，并利用它们进行人类行为识别。这种算法基于人类关节位置的时间序列表示而对动态骨骼建模，并将图卷积扩展为时空图卷积网络而捕捉这种时空的变化关系。

近年来，人类行为识别已经成为一个活跃的研究领域，它在视频理解中起着重要的作用。一般而言，人类行为识别有着多种模态（Simonyan and Zisserman 2014; Tran et al. 2015; Wang, Qiao, and Tang 2015; Wang et al. 2016; Zhao et al. 2017），例如外观、深度、光流和身体骨骼（Du, Wang, and Wang 2015; Liu et al. 2016）等。在这些模态当中，动态人类骨骼通常能与其他模态相辅相成，传达重要信息。然而，比起外观和光流建模，动态骨骼建模受到的关注较少。在这项工作中，我们系统地研究这种模态，旨在开发一种原则性且有效的方法模拟动态骨骼，并利用它们进行人类行为识别。

在 2D 或 3D 坐标形式下，动态骨骼模态可以自然地由人类关节位置的时间序列表示。然后，通过分析其动作模式可以做到人类行为识别。早期基于骨骼进行动作识别的方法只是在各个时间步骤使用关节坐标形成特征向量，并对其进行时序分析 (Wang et al. 2012; Fernando et al. 2015)。但这些方法能力有限，因为它们没有明确利用人类关节的空间关系，而这种空间关系对理解人类行为而言至关重要。最近，研究者开发了试图利用关节间自然连接的新方法 (Shahroudy et al. 2016; Du, Wang, and Wang 2015)。这些方法的改进令人鼓舞，表明了骨骼连通性的重要性。然而，现有的大多数方法依赖手动划分的部分或手动设定的规则来分析空间模式。因此，为特定应用设计的模型难以在其他任务中推广。

图 1：以上是本文所提出的骨骼序列的时空图，其中用到了所提出的 ST-GCN 操作。蓝点代表身体关节。身体关节之间的体内边（intra-body edge）根据人体自然连接定义。帧间边（inter-frame）连接相邻帧之间的相同关节。ST-GCN 中输入的是联合坐标。

为了跨越上述限制，我们需要一种新方法自动捕捉关节的空间构型、时间动态中所嵌入的模式。这就是深度神经网络的力量。然而，如前所述，骨骼并未以 2D 或 3D 网格的方式展现，而是以图像的形式展现。这就使得使用诸如卷积网络等已证实的模型变得困难。最近，将卷积神经网络（CNN）泛化到任意结构图形的图卷积网络（GCN）得到了越来越多的关注，而且被成功应用于图像分类 (Bruna et al. 2014)、文献分类 (Defferrard, Bresson, and Vandergheynst 2016)、半监督学习 (Kipf and Welling 2017) 等领域。但是，顺着这条思路，大部分前人的工作都把输入假定为一个固定的图形。GCN 在大规模数据集上的动态图模型应用，例如人类骨骼序列，还有待探索。

 

                              ST-GCN 最末卷积层的响应可视化结果图 

基于骨架关键点的动作识别

随着如 Microsoft Kinect、OpenPose 等人体姿态检测系统的成熟，基于骨架关键点的人类动作识别成了计算机视觉，特别是人类动作识别研究中的一个重要任务。该任务要求输入在连续的视频帧中检测到的人体骨架关键点序列，输出正在发生的人类动作类别。作为动作识别系统中的重要模态，基于骨架的动作识别已经展现出重要的实用价值与研究价值。本论文正是针对这个任务提出了一种全新的深度学习模型，我们称之为「时空图卷积网络」（ST-GCN）。

 

在本文中，我们通过将图卷积网络扩展到时空图模型，设计用于行为识别的骨骼序列通用表示，称为时空图卷积网络（ST-GCN）。如图 1 所示，该模型是在骨骼图序列上制定的，其中每个节点对应于人体的一个关节。图中存在两种类型的边，即符合关节的自然连接的空间边（spatial edge）和在连续的时间步骤中连接相同关节的时间边（temporal edge）。在此基础上构建多层的时空图卷积，它允许信息沿着空间和时间两个维度进行整合。

ST-GCN 的层次性消除了手动划分部分或遍历规则的需要。这不仅能获得更强的表达能力和更高的性能（如我们的实验所示），而且还使其易于在不同的环境中推广。在通用 GCN 公式化的基础上，我们还基于图像模型的灵感研究设计了图卷积核的新策略。

这项工作的主要贡献在于三个方面：1）我们提出 ST-GCN，一个基于图的动态骨骼建模方法，这是首个用以完成本任务的基于图形的神经网络的应用。2）我们提出了在 ST-GCN 中设计卷积核的几个原则，旨在满足骨骼建模的具体要求。3）在基于骨骼动作识别的两个大规模数据集上，我们的模型与先前使用的手动分配部分或遍历规则的方法相比，需要相当少的手动设计，实现了更优越的性能。ST-GCN 的代码和模型已公开发布 1。

构建时空图

ST-GCN 的基础是时空图结构。从骨架关键点序列构建时空图 (spatial-temporal graph) 的想法来源于我们对现有的骨架动作识别方法以及图像识别方法的观察。我们发现，现有的基于骨架的动作识别方法中为了提高识别精度多数引入了一些空间结构信息，包括相邻关键点的连接关系或身体部件等（如手-手肘-肩膀的连接关系）。

为了建模这些空间信息，现有方法常常使用 RNN 等序列模型来遍历相连的关键点。这就要求模型设计者定义一种遍历的规则，或者手动定义一些身体部件。我们指出，在这种设计中，很难得到一个最优的遍历规则或者部件划分。但是，我们发现，关键点之间天然的连接关系，其实构成了一个天然的图结构（graph）。那么，我们怎么能够高效地使用这些图结构来进行动作识别呢？

在 ST-GCN 的工作中我们提出，可以从输入的关键点序列中建立一个时空图（spatial-temporal graph）。这个图结构按照如下的规则来构建。

 

1. 在每一帧内部，按照人体的自然骨架连接关系构造空间图；

2. 在相邻两帧的相同关键点连接起来，构成时序边；

3. 所有输入帧中关键点构成节点集（node set），步骤 1、2 中的所有边构成边集（edge set），即构成所需的时空图。

 

在按照上述规则得到的时空图上，我们自然地保留了骨架关键点的空间信息，并使得关键点的运动轨迹（trajectory）以时序边的形式得到表现。这使得我们可以设计一个统一的模型来完整地对这些信息进行建模。在图 1中我们展示了一种时空图的结构。

 

图结构上的卷积网络

为了在时空图上对人类动作的信息进行分析，我们提出使用图卷积网络 (graph convolutional networks – GCN)。图上的神经网络模型是机器学习研究的一个热点领域。本文中使用的图卷积网络即是图上神经网络中的一种，其在网络分析、文本分类等问题都有成功应用。

在介绍图卷积网络的概念之前，我们先来回顾图像上的卷积操作。在图像上，卷积操作使用一些固定大小的卷积核（filter/kernel）来扫描输入的图像。如图 3 所示，在每个扫描的中心位置像素附近，抽取一个与权重矩阵大小相同的像素矩阵，将这些像素上的特征向量按空间顺序拼接并与卷积核的参数向量做内积以得到该位置的卷积输出值。在这里，「附近像素」可以定义为像素网格（grid）上的一个邻域（neighborhood）。将图像上的卷积操作推广到任意结构的图结构上时，我们同样可以定义任何一个节点的邻域，与一系列权重矩阵。这就是图卷积网络的基本思想。

但是，与图像不同的是，普通的图结构上如果使用邻接矩阵（Adjacency matrix）来定义邻域时，每个节点的邻域中节点的数量并不是固定的（考虑补 0 时，图像上像素附近的像素是总是固定的）。这就使得我们我们很难确定： 1）需要使用的卷积核的参数维度；2）如果排列权重矩阵与邻域内的节点以进行内积运算。在原始的 GCN 文章中，作者提出了将内积操作变为这样一个操作：使用同一个向量与所有邻域内的点上的特征向量计算内积并将结果求均值。这使得： 1）卷积核的参数可以确定为一个固定长度的向量；2）不需要考虑邻域内节点的顺序。这个设计使得 GCN 可以在任意连接关系的图上使用，并在一些任务，如网络分析和半监督学习中取得了较好的性能。

需要注意的是，图上神经网络除了上面提到基于图的空间结构的思路之外，还有一种基于谱分析 (spectral analysis) 的构造思路。关于这一类方法，请见参考文献【2】。在 ST-GCN 中，我们也使用了基于图的空间结构的思路。

时空图卷积网络与动作识别

要将图卷积网络运用于基于骨架关键点的动作识别中，我们还需要仔细分析这个任务的特点与难点，而不是直接将已有方法生搬硬凑。在本文中，我们指出了原始 GCN 的一个重要性质：该文中提出的卷积操作，实质上等价于先将邻域内所有节点的特征向量求平均，再与卷积核的参数向量计算内积。这种平均操作在骨架动作识别会遇到一个重要问题，即：它无法建模关键点之间相对位置变化的情况，或所谓的「微分性质」（differential properties）。因此基于原始 GCN 的模型，识别性能并不会很理想。

针对这个问题，我们认为，要真正增强的模型的性能，必须跳出原始 GCN 的「平均思想」。为了解决这个问题，我们将理解了图像上的卷积操作理解为把中心像素相邻的像素集合（邻域集-neighbor set）按照空间顺序，如从左至右，从上至下，划分为一系列集合。在图像的情形中，每个集合正好包含一个像素。这些集合就构成了邻域集的一个划分（partition）。卷积核的参数只与这个划分中的子集个数以及特征向量长度有关。那么在普通的图结构中，只要定义了某种划分规则（partitioning strategy），我们就也可以参照图像卷积来定义卷积核的参数。类似的思想也应用在了如 deformable CNN 等近期工作中。

有了这个思想，我们就可以针对骨架动作识别，乃至任何图卷积网络所面对的问题来定义有针对性的卷积操作。而定义卷积操作就简化为了设计对应的划分规则。对一个存在 K 个子集的划分规则，卷积核的参数包含 K 个部分，每个部分参数数量与特征向量一样。仍然以图像上的卷积为例，在一个窗口大小为 3x3 的卷积操作中，一个像素的邻域（窗口）按照空间顺序被划分为 9 个子集（左上，上，右上，左，中，右，左下，下，右下），每个子集包含一个像素。卷积核的参数包含 9 个部分，每个部分与特征图（feature map）的特征向量长度（number of channel）一致。也就是说，图像卷积可以解释为普通图上卷积在规则网格图（regular grid）上的一种应用。

为了在时空图上进行骨架动作识别，我们提出了三种空间的划分规则。

第一种称为「唯一划分」(uni-labeling)。其与原始 GCN 相同，将节点的 1 邻域划分为一个子集。

第二种称为「基于距离的划分」(distance partitioning)，它将节点的 1 邻域分为两个子集，即节点本身子集与邻节点子集。引入基于距离的划分使得我们可以分析骨架关键点之间的微分性质。

进一步，我们针对动作识别的特点，提出了第三种，「空间构型划分」(spatial configuration partitioning)。这种划分规则将节点的 1 邻域划分为 3 个子集，第一个子集为节点本身，第二个为空间位置上比本节点更靠近整个骨架重心的邻节点集合，第三个则为更远离重心的邻节点集合。建立这种划分规则在根据运动分析的研究中对向心运动与离心运动的定义。三种划分规则的示意图请见图 3。

 

流程概览

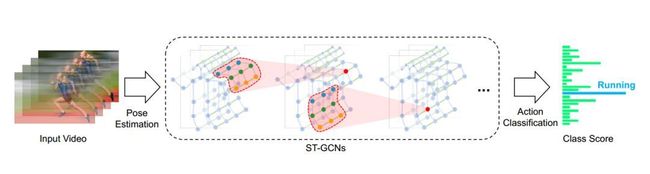
基于骨骼的数据可以从运动捕捉设备或视频的姿态估计算法中获得。通常来说，数据是一系列的帧，每一帧都有一组联合坐标。给定 2D 或 3D 坐标系下的身体关节序列，我们就能构造一个时空图。其中，人体关节对应图的节点，人体身体结构的连通性和时间上的连通性对应图的两类边。因此，ST-GCN 的输入是图节点的联合坐标向量。这可以被认为是一个基于图像的 CNN 模拟，其中输入由 2D 图像网格上的像素强度矢量形成。对输入数据应用多层的时空图卷积操作，可以生成更高级别的特征图。然后，它将被标准的 SoftMax 分类器分类到相应的动作类别。整个模型用反向传播进行端对端方式的训练。现在，我们将介绍 ST-GCN 模型的各个部分。

图 2：我们对视频进行姿态估计，并在骨骼序列上构建时空图。此后，对其应用多层时空图卷积操作（ST-GCN），并逐渐在图像上生成更高级的特征图。然后，利用标准的 Softmax 分类器，能将其分类到相应的操作类别中。

图 3：本文提出的用于构建卷积操作的分割策略。从左到右：（a）输入骨骼的框架示例。身体关节以蓝点表示。D=1 的卷积核感受野由红色的虚线画出。（b）单标签划分策略。其中近邻的所有节点标签相同（绿色）。（c）距离划分。这两个子集是距离为 0 的根节点本身，和距离为 1 的根节点相邻节点（蓝色）。（d）空间构型划分。根据节点到骨架重心（图中黑色十字）的距离和到根节点（绿色）的距离的比较进行标记。向心节点（蓝色）到骨架重心的距离比根节点到骨架重心的距离短，而离心节点（黄色）到骨架重心的距离比根节点长。

 

除了同一帧内部的空间划分规则，在时间上，由于时序边构成了一个网格，我们可以直接使用类似于时序卷积（temporal convolution）的划分规则。最终，时空图上使用的划分规则得到的子集集合会是空间划分与时序划分的笛卡尔积。

定义好了时空图上的卷积操作，我们就可以设计卷积网络了。为了展示 ST-GCN 的性能，我们直接从一个已有的时序卷积网络结构的基础上设计了文中用到的 ST-GCN 的网络结构。我们将所有时序卷积操作转为时空图的卷积操作，每一个卷积层的输出是一个时空图，图上每一个节点保有一个特征向量。最终，我们合并所有节点上的特征并使用线性分类层进行动作分类。训练使用标准的 SoftMax 交叉熵损失函数进行监督。参数学习使用标准随机梯度下降算法（SGD）。

实验结果

我们在两个性质迥异的骨架动作识别数据集上进行了实验来验证 ST-GCN 的性能。

第一个数据集是 Kinetics-Skeleton，它来自于最近由 Google DeepMind 贡献的 Kinetics 视频人类动作识别数据集。我们使用 OpenPose 姿态估计软件得到视频中所有的骨架关键点信息来构成 Kinetics-Skeleton。该数据集共有约 30 万个视频与 400 类动作。

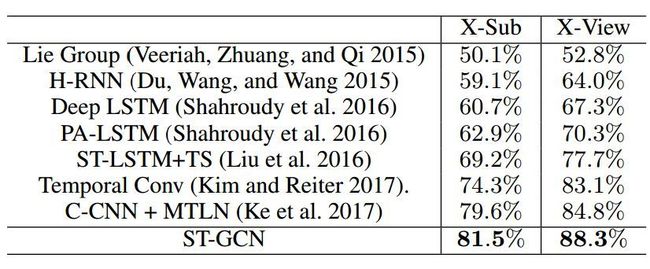
第二个数据集是 NTU-RGB+D，这是三维骨架动作识别的标准测试数据集。它包含了用 Microsoft Kinect 采集的三维骨架序列。该数据集共有约 6 万个视频，60 个动作类别。这个数据集包含了两个测试协议，即跨表演人（X-Sub）与跨视角（X-View）协议。在两个数据集的三个测试协议上，ST-GCN 相比现有方法在识别精度上均有很大提高，具体结果可见表图 。

 

表 2：基于骨骼的模型在动力学数据集（Kinetics dataset）中的动作识别性能。在表格顶部，我们列出了基于帧的方法的性能。

表 3：基于骨骼的模型在 NTU-RGB+D 数据集上的动作识别性能。本文根据交叉主题（X-Sub）和交叉视图（X-View）的基准进行准确率计算。

除了得到更好的性能，我们也详细分析了三种划分规则对识别精度的影响。如表 2 所示，正如我们所期望的，距离划分与空间构型划分相对于原始 GCN 使用的唯一划分在精度上均有较大提高。这证明了引入新的划分规则的重要性。特别的，针对动作识别任务设计的空间构型划分取得了最高的性能，并被最后应用于 ST-GCN 的相关实验中。

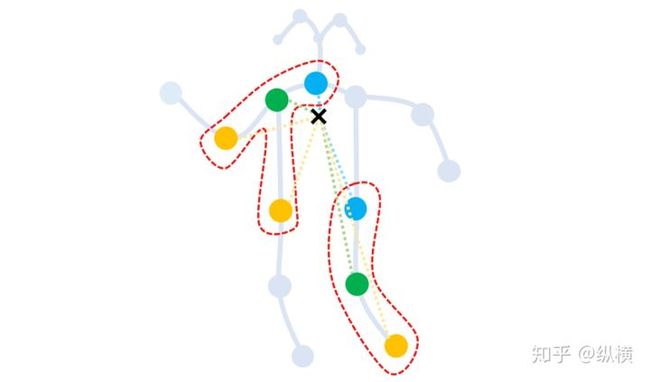
我们还将 ST-GCN 的最后一层神经元响应进行了可视化（表 2）。在结果中我们可以明显看到 ST-GCN 能够追踪并深入分析在某个时间段与动作最相关的身体部分的运动，这解释了为何 ST-GCN 相对于其他不关注空间结构的现有方法能得到很大的性能提高。

 

 

 

 

 

论文：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

论文链接：https://arxiv.org/abs/1801.07455

github:https://github.com/yysijie/st-gcn

思考与最后的话

人体骨骼动力学为人类行为识别提供了重要信息。传统的骨骼建模方法通常依赖手动划分部分或遍历规则，导致模型表达能力有限、泛化困难。在这项工作当中，我们提出了一个名为时空图卷积网络（ST-GCN）的新型动态骨骼模型，它通过自主学习数据中的时间、空间模式，超越了以往方法的局限性，具有更强的表现力和泛化能力。在 Kinetics 和 NTU-RGBD 两大数据集中，本模型与主流方法相比有了很大的提高。

回顾 ST-GCN 的提出，我们总结了两个重要的思想跨越。

第一个是从将骨架序列理解为一帧帧的骨架演进为将整个视频理解为一个整体的时空图，这使得用一个统一的模型来分析动作成为可能。第二个是从原始 GCN 的朴素思想演进为使用基于划分规则的卷积定义。这个思想使得我们可以超越原始 GCN 并得到巨大的性能提升，该思想也在 MoNet【3】的工作中被提及过。我们将其原则化为 集合的划分操作。这也使得这个思想可以应用其他的分析任务中。

用大粗话来说，作者的主要工作就两点：

• 使用 OpenPose 处理了视频，提出了一个数据集
• 结合 GCN 和 TCN 提出了模型，在数据集上效果还不错

在将来的工作中，我们计划运用 ST-GCN 的灵活性来处理更多的图分析问题。同时，针对动作识别任务，一个自然的演进就是在骨架关键点坐标的基础上引入视觉特征，如图像特征，乃至场景图（scene-graph）等，并将它们统一在 ST-GCN 的分析框架下。我们的最终目标则是一个性能更高，更具有可解释性的统一的视频动作识别模型。

 

作者：纵横
链接：https://www.zhihu.com/question/276101856/answer/638672980
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

OpenPose 预处理

OpenPose 是一个标注人体的关节（颈部，肩膀，肘部等），连接成骨骼，进而估计人体姿态的算法。作为视频的预处理工具，我们只需要关注 OpenPose 的输出就可以了。

视频中的骨骼标注

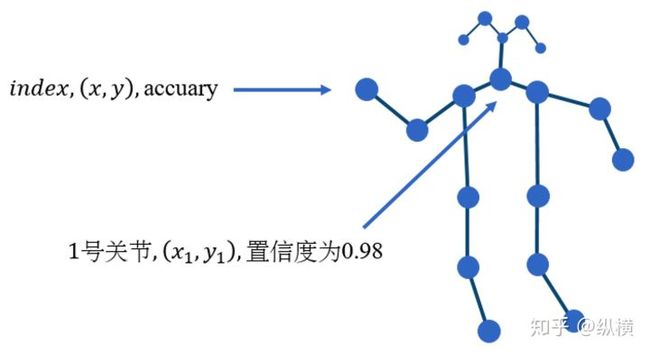
总的来说，视频的骨骼标注结果维数比较高。在一个视频中，可能有很多帧（Frame）。每个帧中，可能存在很多人（Man）。每个人又有很多关节（Joint）。每一个关节又有不同特征（位置、置信度）。

关节的特征

对于一个 batch 的视频，我们可以用一个 5 维矩阵 表示。

• 代表视频的数量，通常一个 batch 有 256 个视频（其实随便设置，最好是 2 的指数）。
• 代表关节的特征，通常一个关节包含 等 3 个特征（如果是三维骨骼就是 4 个）。
• 代表关键帧的数量，一般一个视频有 150 帧。
• 代表关节的数量，通常一个人标注 18 个关节。
• 代表一帧中的人数，一般选择平均置信度最高的 2 个人。
• 所以，OpenPose 的输出，也就是 ST-GCN 的输入，形状为 。

想要搞 End2End 的同学还是要稍微关注一下 OpenPose 的实现的。最近还有基于 heatmap 的工作，效果也不错~

ST-GCN 网络结构

论文中给出的模型描述很丰满，要是只看骨架，网络结构如下：

ST-GCN 网络结构

主要分为三部分：

归一化

首先，对输入矩阵进行归一化，具体实现如下：

N, C, T, V, M = x.size()
# 进行维度交换后记得调用 contiguous 再调用 view 保持显存连续
x = x.permute(0, 4, 3, 1, 2).contiguous()
x = x.view(N * M, V * C, T)
x = self.data_bn(x)
x = x.view(N, M, V, C, T)
x = x.permute(0, 1, 3, 4, 2).contiguous()
x = x.view(N * M, C, T, V)

归一化是在时间和空间维度下进行的（ ）。也就是将一个关节在不同帧下的位置特征（x 和 y 和 acc）进行归一化。

这个操作是利远大于弊的：

• 关节在不同帧下的关节位置变化很大，如果不进行归一化不利于算法收敛
• 在不同 batch 不同帧下的关节位置基本上服从随机分布，不会造成不同 batch 归一化结果相差太大，而导致准确率波动。

时空变换

接着，通过 ST-GCN 单元，交替的使用 GCN 和 TCN，对时间和空间维度进行变换：

# N*M(256*2)/C(3)/T(150)/V(18)
Input：[512, 3, 150, 18]
ST-GCN-1：[512, 64, 150, 18]
ST-GCN-2：[512, 64, 150, 18]
ST-GCN-3：[512, 64, 150, 18]
ST-GCN-4：[512, 64, 150, 18]
ST-GCN-5：[512, 128, 75, 18]
ST-GCN-6：[512, 128, 75, 18]
ST-GCN-7：[512, 128, 75, 18]
ST-GCN-8：[512, 256, 38, 18]
ST-GCN-9：[512, 256, 38, 18]

空间维度是关节的特征（开始为 3），时间的维度是关键帧数（开始为 150）。在经过所有 ST-GCN 单元的时空卷积后，关节的特征维度增加到 256，关键帧维度降低到 38。

个人感觉这样设计是因为，人的动作阶段并不多，但是每个阶段内的动作比较复杂。比如，一个挥高尔夫球杆的动作可能只需要分解为 5 步，但是每一步的手部、腰部和脚部动作要求却比较多。

read out 输出

最后，使用平均池化、全连接层（或者叫 FCN）对特征进行分类，具体实现如下：

# self.fcn = nn.Conv2d(256, num_class, kernel_size=1)

# global pooling
x = F.avg_pool2d(x, x.size()[2:])
x = x.view(N, M, -1, 1, 1).mean(dim=1)
# prediction
x = self.fcn(x)
x = x.view(x.size(0), -1)

Graph 上的平均池化可以理解为对 Graph 进行 read out，即汇总节点特征表示整个 graph 特征的过程。这里的 read out 就是汇总关节特征表示动作特征的过程了。通常我们会使用基于统计的方法，例如对节点求 等等。mean 鲁棒性比较好，所以这里使用了 mean。

插句题外话，这里的 卷积和全连接层等效，最近在用 matconvnet 的时候，发现它甚至不提供全连接层，只使用 的卷积。

GCN

从结果上看，最简单的图卷积似乎已经能取得很好的效果了，具体实现如下：

def normalize_digraph(A):
    Dl = np.sum(A, 0)
    num_node = A.shape[0]
    Dn = np.zeros((num_node, num_node))
    for i in range(num_node):
        if Dl[i] > 0:
            Dn[i, i] = Dl[i]**(-1)
    AD = np.dot(A, Dn)
    return AD

作者在实际项目中使用的图卷积公式就是：

公式可以进行如下化简：

其实就是以边为权值对节点特征求加权平均。其中， 可以理解为卷积核。如果不了解图卷积可以看这里。

归一化的加权平均法

Multi-Kernal

考虑到动作识别的特点，作者并未使用单一的卷积核，而是使用『图划分』，将 分解成了 。（作者其实提出了几种不同的图划分策略，但是只有这个比较好用）

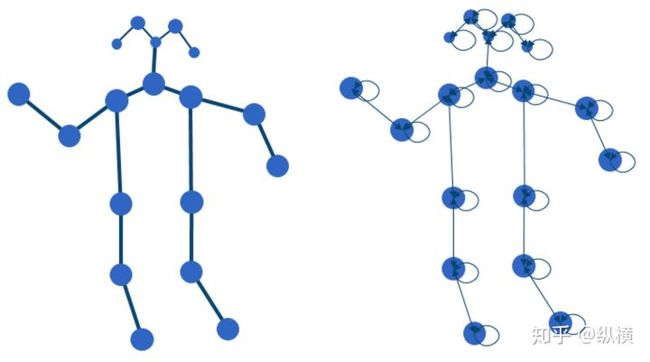
原始图

表示的所有边如上图右侧所示：

• 两个节点之间有一条双向边
• 节点自身有一个自环

作者结合运动分析研究，将其划分为三个子图，分别表达向心运动、离心运动和静止的动作特征。

子图划分方法

对于一个根节点，与它相连的边可以分为 3 部分。

• 第 1 部分连接了空间位置上比本节点更远离整个骨架重心的邻居节点（黄色节点），包含了离心运动的特征。
• 第 2 部分连接了更为靠近重心的邻居节点（蓝色节点），包含了向心运动的特征。
• 第 3 部分连接了根节点本身（绿色节点），包含了静止的特征。

子图划分结果

使用这样的分解方法，1 个图分解成了 3 个子图。卷积核也从 1 个变为了 3 个，即 变为 。3 个卷积核的卷积结果分别表达了不同尺度的动作特征。要得到卷积的结果，只需要使用每个卷积核分别进行卷积，在进行加权平均（和图像卷积相同）。

具体实现如下：

A = []
for hop in valid_hop:
    a_root = np.zeros((self.num_node, self.num_node))
    a_close = np.zeros((self.num_node, self.num_node))
    a_further = np.zeros((self.num_node, self.num_node))
    for i in range(self.num_node):
        for j in range(self.num_node):
            if self.hop_dis[j, i] == hop:
                if self.hop_dis[j, self.center] == self.hop_dis[
                        i, self.center]:
                    a_root[j, i] = normalize_adjacency[j, i]
                elif self.hop_dis[j, self.
                                  center] > self.hop_dis[i, self.
                                                         center]:
                    a_close[j, i] = normalize_adjacency[j, i]
                else:
                    a_further[j, i] = normalize_adjacency[j, i]
    if hop == 0:
        A.append(a_root)
    else:
        A.append(a_root + a_close)
        A.append(a_further)
A = np.stack(A)
self.A = A

Multi-Kernal GCN

现在，我们可以写出带有 个卷积核的图卷积表达式了：

表达式可以用爱因斯坦求和约定表示 。其中，

• 表示所有视频中的人数（batch * man）
• 表示卷积核数（使用上面的分解方法 k=3）
• 表示关节特征数（64 ... 128）
• 表示关键帧数（150 ... 38）
• 和 表示关节数（使用 OpenPose 的话有 18 个节点）

对 求和代表了节点的加权平均，对 求和代表了不同卷积核 feature map 的加权平均，具体实现如下：

# self.conv = nn.Conv2d(
#             in_channels,
#             out_channels * kernel_size,
#             kernel_size=(t_kernel_size, 1),
#             padding=(t_padding, 0),
#             stride=(t_stride, 1),
#             dilation=(t_dilation, 1),
#             bias=bias)

x = self.conv(x)
n, kc, t, v = x.size()
x = x.view(n, self.kernel_size, kc//self.kernel_size, t, v)
x = torch.einsum('nkctv,kvw->nctw', (x, A))
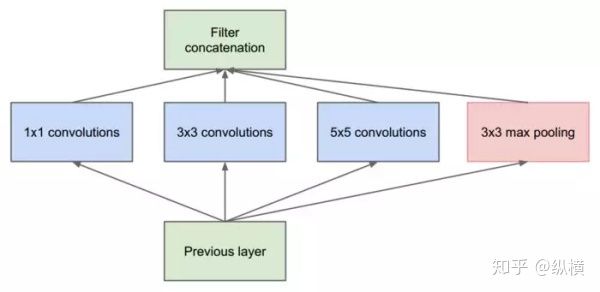
return x.contiguous(), A

如果要类比的话，其实和 GoogleNet 的思路有些相似：

都在一个卷积单元中试图利用不同感受野的卷积核，提取不同分量的特征。

GoogleNet

TCN

GCN 帮助我们学习了到空间中相邻关节的局部特征。在此基础上，我们需要学习时间中关节变化的局部特征。如何为 Graph 叠加时序特征，是图网络面临的问题之一。这方面的研究主要有两个思路：时间卷积（TCN）和序列模型（LSTM）。

ST-GCN 使用的是 TCN，由于形状固定，我们可以使用传统的卷积层完成时间卷积操作。为了便于理解，可以类比图像的卷积操作。st-gcn 的 feature map 最后三个维度的形状为 ，与图像 feature map 的形状 相对应。

• 图像的通道数 对应关节的特征数 。
• 图像的宽 对应关键帧数 。
• 图像的高 对应关节数 。

在图像卷积中，卷积核的大小为『w』 『1』，则每次完成 w 行像素，1 列像素的卷积。『stride』为 s，则每次移动 s 像素，完成 1 行后进行下 1 行像素的卷积。

时间卷积示意图

在时间卷积中，卷积核的大小为『temporal_kernel_size』 『1』，则每次完成 1 个节点，temporal_kernel_size 个关键帧的卷积。『stride』为 1，则每次移动 1 帧，完成 1 个节点后进行下 1 个节点的卷积。

具体实现如下：

padding = ((kernel_size[0] - 1) // 2, 0)

self.tcn = nn.Sequential(
    nn.BatchNorm2d(out_channels),
    nn.ReLU(inplace=True),
    nn.Conv2d(
        out_channels,
        out_channels,
        (temporal_kernel_size, 1),
        (1, 1),
        padding,
    ),
    nn.BatchNorm2d(out_channels),
    nn.Dropout(dropout, inplace=True),
)

再列举几个序列模型的相关工作，感兴趣的同学可以尝试一下：

• AGC-Seq2Seq 使用的是 Seq2Seq + Attention。
• ST-MGCN 使用的是 CGRNN。
• DCRNN 使用的是 GRU。

Attention

作者在进行图卷积之前，还设计了一个简易的注意力模型（ATT）。如果不了解图注意力模型可以看这里。

# 注意力参数
# 每个 st-gcn 单元都有自己的权重参数用于训练
self.edge_importance = nn.ParameterList([
    nn.Parameter(torch.ones(self.A.size()))
    for i in self.st_gcn_networks
])
# st-gcn 卷积
for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
    print(x.shape)
    # 关注重要的边信息
    x, _ = gcn(x, self.A * importance)

其实很好理解，在运动过程中，不同的躯干重要性是不同的。例如腿的动作可能比脖子重要，通过腿部我们甚至能判断出跑步、走路和跳跃，但是脖子的动作中可能并不包含多少有效信息。

因此，ST-GCN 对不同躯干进行了加权（每个 st-gcn 单元都有自己的权重参数用于训练）。

 

 

 

附（知识扩充）：

如何理解 Graph Convolutional Network（GCN）？

如何通俗易懂地解释卷积？

图像傅里叶变换的物理意义：

 

 

关于傅里叶变换，参见深入浅出的讲解傅里叶变换

傅里叶变换就是这么简单，你学会了吗? 

 

 

参考文献：

1.https://blog.csdn.net/qq_36893052/article/details/79860328

2.https://www.sohu.com/a/220023474_129720

3.https://baijiahao.baidu.com/s?id=1592524811793369516&wfr=spider&for=pc

4.https://www.zhihu.com/question/276101856/answer/638672980

5.https://www.zhihu.com/question/54504471/answer/611222866