AVL树(平衡二叉树)与红黑树(RBTree)的对比
(一)简介
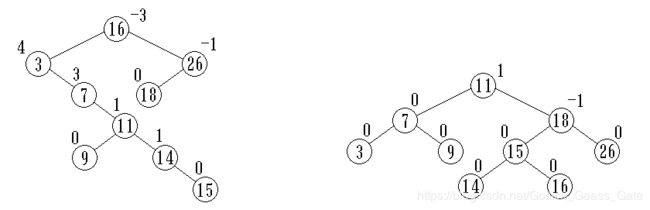
1. AVL树:一棵AVL树或者是空树,或者是具有下列性质的二叉查找树——它的左子树和右子树都是AVL树,且左子树和右子树的高度之差的绝对值不超过1。e.g.
高度不平衡的二叉排序树 高度平衡的二叉查找树(AVL树)
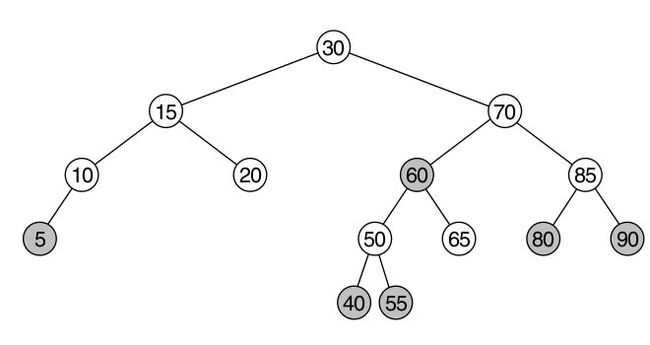
2. 红黑树是一种二叉树,同时它还满足下列5个特性:
- 每个结点是红色或者黑色的。
- 根结点是黑色的。
- 每个空结点(NULL/NIL)是黑色的。(这里将空结点作为一个特殊的结点对待,设定他们必须是黑色的。)
- 如果一个结点是红色的,则它的左右子结点都必须是黑色的。(但黑色结点的子结点可以是黑色的。)
- 对任意一个结点来说,从它到空结点的所有路径必须包含相同数目的黑色结点。
e.g.
3. 和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树)。
(二)旋转
AVL树和红黑树的插入和删除操作都需要通过树的旋转来维持平衡。树的左旋和右旋的过程用一个图来直观地表示:
1. 左旋:父结点![]() 成为右子结点
成为右子结点![]() 的左子结点,
的左子结点,![]() 的左子结点成为
的左子结点成为![]() 的右子结点。
的右子结点。
2. 右旋:父结点![]() 成为左子结点
成为左子结点![]() 的右子结点,
的右子结点,![]() 的右子结点成为
的右子结点成为![]() 的左子结点。
的左子结点。
(三)AVL树插入结点之后的调整
从最底层的违反平衡条件的结点以下的三个结点开始,
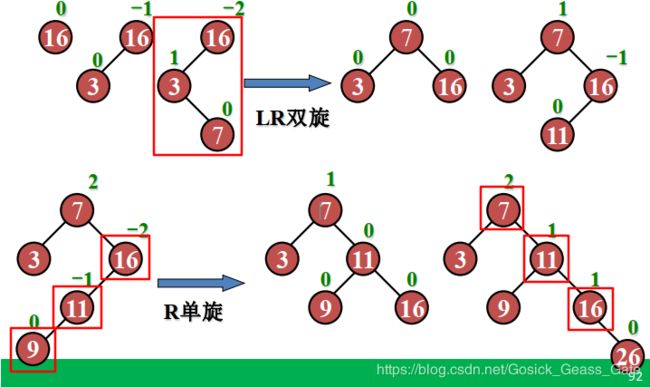
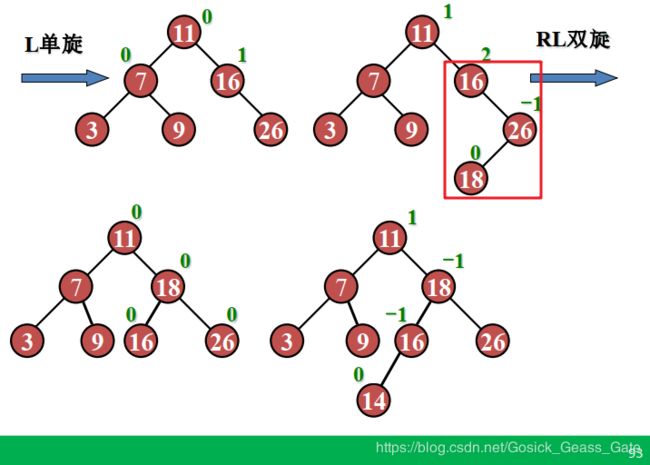
1. 单旋:如果这三个结点连成一条直线,则直接旋转即可。旋转规则如下:
- 直线方向为“左下——右上”,则右旋;
- 直线方向为“左上——右下”,则左旋。
2. 双旋:如果是形成一个转角,则需先旋转成直线,再按照单旋的情形旋转。
e.g. 输入关键字序列为 { 16, 3, 7, 11, 9, 26, 18, 14, 15 },插入和调整过程如下:
(四)红黑树插入结点之后的调整
为新加入的结点N赋予红色(如果赋予黑色则一定会违反红黑树的条件5,而赋予红色则只有在父结点或子结点为红色的时候才会违反红黑树的条件4,调整的概率比前者小)。
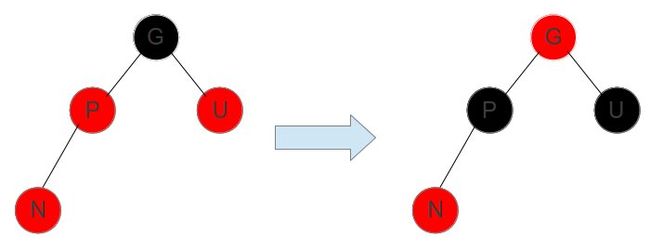
1. 情形一:N节点的父节点P以及P的兄弟节点都是红色,而它的祖父节点G为黑色。
P(红变黑)、G(黑变红)、U(红变黑)
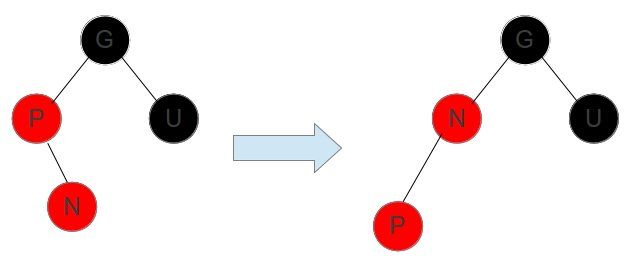
2. 情形二:N节点的父节点P是红色,但是它的祖父节点G和它父节点的兄弟节点U为黑色。
(1)先左旋:
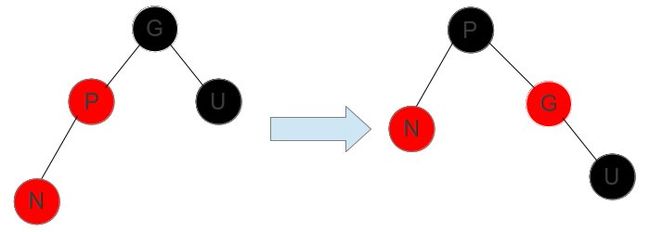
(2)再右旋:P(红变黑)、G(黑变红)
(五)红黑树删除结点之后的结点继承
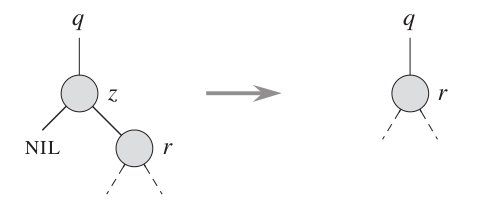
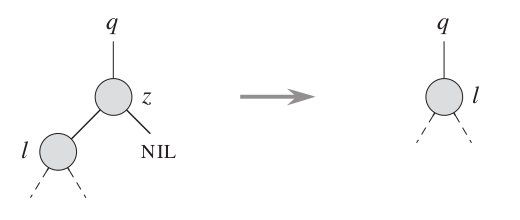
1. 待删除节点没有子节点,则直接删除该节点。
2. 待删除节点只有一个子节点,则用该子节点替换它的父节点。
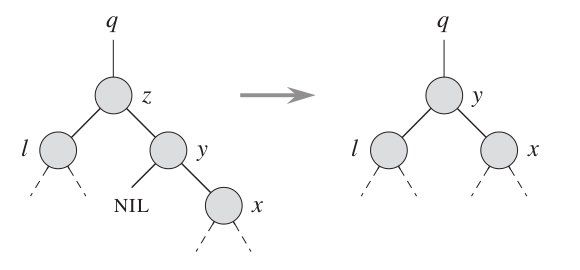
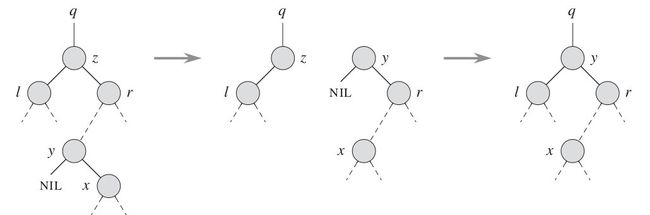
3. 待删除节点有两个子节点,则取它的后继节点替换它,并删除这个后继节点原来的位置。它可能有两种情况:
不过不难发现,其实质就是使用中序遍历的后继结点来继承被删除的结点,而且该后继结点最多只有一个子结点,可以理解为将后继结点的值复制到被删除结点的位置,然后再删除该后继结点,也就是转换成了上面的第2种类型。
(六)红黑树删除结点之后的调整
仅仅依靠节点继承得到的红黑树可能是不平衡的,需要进一步调整。而且由(五)可知,删除结点有两个子结点的情况都可以转换成删除结点只有一个子结点的情况,所以下面我们只需讨论删除结点只有一个子结点的情况。
假设删除的结点是红色的,那其子结点一定是黑色的,直接继承即可,无需赘言。
假设删除的结点是黑色的,现在又面临着两种情况:
- 如果子结点是红色的,则可以使它变成黑色然后直接继承;
- 如果子结点是黑色的,继承之后则依然会破坏条件5,需要进一步调整使得继承结点所在的子树黑色结点数+1或者其兄弟结点(实际上是被删除结点的兄弟)所在的子树黑色结点数-1。所以下面我们可以将讨论的范围缩小为:删除结点只有一个子结点且该子结点为黑色的情况。
记代替删除结点的子结点为N,N的新的父结点为P,N的兄弟结点为S, S的左孩子为L,S的右孩子为R。
下面可以分5种情况进行讨论:
1. 情形一:P是红色的,S和S的两个子结点L、R都是黑色的。
P(红变黑)、S(黑变红)
2. 情形二:P的颜色无关(don't care),S和它的左子结点L是黑色的,S的右子结点R是红色的。
先左旋,然后S(变成P的颜色)、P(变黑)、R(红变黑)
3. 情形三:P的颜色无关(don't care),S和它的右子结点R是黑色的,S的左子结点L是红色的。
直接右旋,就可以转换为情形二。
4. 情形四:P是黑色的,S是红色的,那么自然S的两个子结点L、R都是黑色的。
先左旋,P(黑变红),S(红变黑)
5. 情形五:P、S、L、R都是黑色的。
S(黑变红)
(七)总结
AVL树适合用于插入与删除次数比较少,但查找多的情况;相对于要求严格的AVL树来说,红黑树的旋转次数少,所以对于搜索、插入、删除操作较多的情况下,我们就用红黑树。
红黑树广泛应用于C++的STL中,e.g. set、multiset、map、multimap;另外,Java的TreeMap和TreeSet也是使用红黑树来实现的。
参考博客:
【1】Java集合类深入分析之TreeMap/TreeSet篇
【2】【STL】STL中红黑树的应用set、multiset、map、multimap
【3】红黑树和AVL树(平衡二叉树)区别
【4】红黑树(二):删除