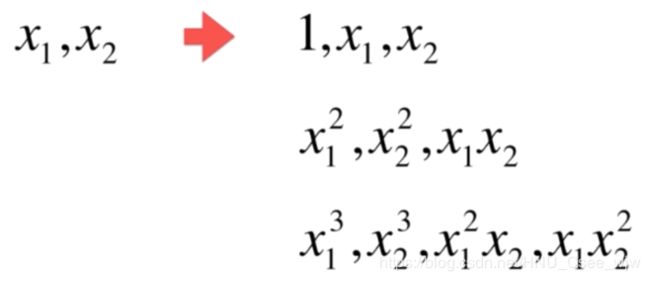Python遇见机器学习 ---- 多项式回归 Polynomial Regression
综述
“寒泉自可斟,况复杂肴醴。”
本文采用编译器:jupyter
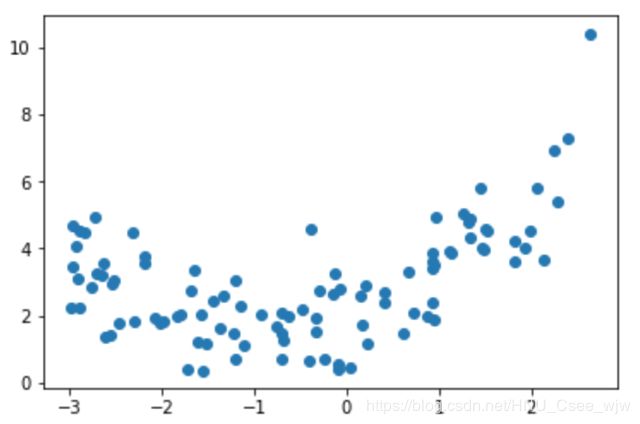
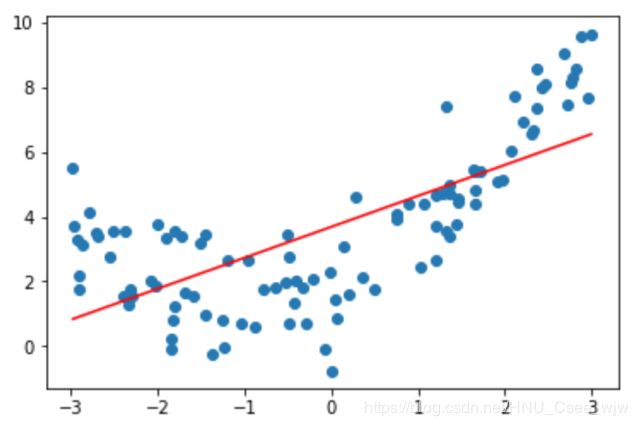
在介绍线性回归模型时,曾假设所有模拟的数据均满足线性关系,即y是x的一次函数,然而现实中极少有这么理想的数据,这是我们就需要考虑更一般化的方法了,其中多项式回归为我们提供了一些思路。
如上图,虽然y是关于x的二次方程,但实际上如果把x平方与x分别看成两个特征就变成我们之前所介绍的线性回归问题。
即,相当于我们对原来的数据增加了一些特征(升维),但本质上还是求的这条曲线。
01 多项式回归
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()# 先查看线性回归的效果
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
# Out[6]:
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
y_predict = lin_reg.predict(X)
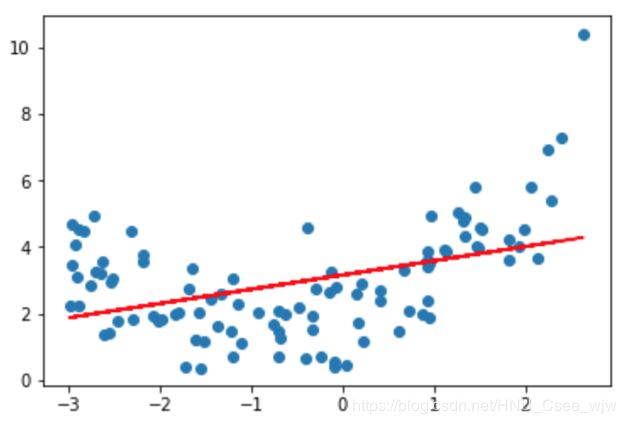
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show() # 可以看到效果并不是很好解决方法,添加一个特征
(X**2).shape
# Out[9]:
# (100, 1)
X2 = np.hstack([X, X**2])
X2.shape
# Out[11]:
# (100, 2)
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
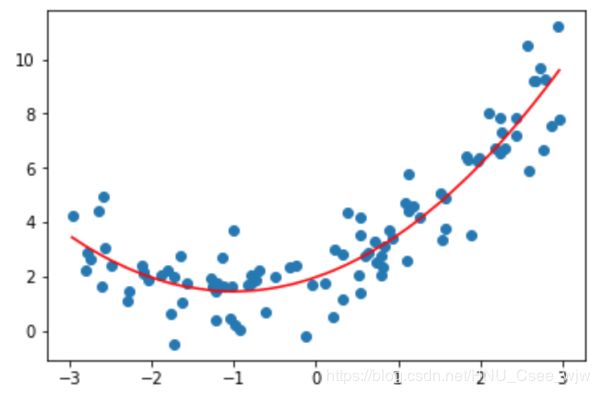
plt.scatter(x, y)
# x是乱序的,我们应该按照x从小到大来绘制
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show() lin_reg2.coef_ # 查看系数a和b
# Out[15]:
# array([ 0.84918223, 0.48009585])
lin_reg2.intercept_ # 查看截距
# Out[16]:
# 1.994242097161812702 scikit-learn中的多项式回归和Pipeline
PolynomialFeatures(degree=3) 中的参数degree表示阶数,计算如下:
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
# 多项式回归最主要的事情是数据预处理
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2) # 添加二次幂特征
poly.fit(X)
X2 = poly.transform(X)
X2.shape
# Out[5]:
# (100, 3)
X2[:5,:] # 第一列是x的0次方,最后一列是x的2次方
# Out[7]:
"""
array([[ 1. , 1.72084082, 2.96129314],
[ 1. , -0.72185736, 0.52107804],
[ 1. , -0.97576562, 0.95211855],
[ 1. , -1.76849693, 3.12758138],
[ 1. , -1.54863002, 2.39825493]])
"""
from sklearn.linear_model import LinearRegression
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
lin_reg2.coef_
# Out[10]:
# array([ 0. , 1.0779785 , 0.55559044])
lin_reg2.intercept_
# Out[11]:
# 1.7321546824053558关于PolynomialFeatures
X = np.arange(1, 11).reshape(-1, 2)
X.shape
# Out[13]:
# (5, 2)
X
"""
Out[14]:
array([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10]])
"""
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)
X2.shape
# Out[16]:
# (5, 6)
# X的平方变成三列,分别是第一列的平方,第一列乘以第二列,第二列的平方
X2
"""
Out[17]:
array([[ 1., 1., 2., 1., 2., 4.],
[ 1., 3., 4., 9., 12., 16.],
[ 1., 5., 6., 25., 30., 36.],
[ 1., 7., 8., 49., 56., 64.],
[ 1., 9., 10., 81., 90., 100.]])
"""
poly = PolynomialFeatures(degree=3)
poly.fit(X)
X3 = poly.transform(X)
X3.shape
# Out[19]:
# (5, 10)
X3
"""
Out[20]:
array([[ 1., 1., 2., 1., 2., 4., 1., 2.,
4., 8.],
[ 1., 3., 4., 9., 12., 16., 27., 36.,
48., 64.],
[ 1., 5., 6., 25., 30., 36., 125., 150.,
180., 216.],
[ 1., 7., 8., 49., 56., 64., 343., 392.,
448., 512.],
[ 1., 9., 10., 81., 90., 100., 729., 810.,
900., 1000.]])
"""Pipeline
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
poly_reg = Pipeline([
("poly", PolynomialFeatures(degree=2)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
03 过拟合,欠拟合
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()使用线性回归
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)
# Out[4]:
# 0.49537078118650091
# 欠拟合
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()# 使用均方误差来评判
from sklearn.metrics import mean_squared_error
y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)
# Out[6]:
# 3.0750025765636577使用多项式回归
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)
"""
Out[8]:
Pipeline(memory=None,
steps=[('poly', PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)), ('std_scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('lin_reg', LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False))])
"""
y2_predict = poly2_reg.predict(X)
# 计算均方误差
mean_squared_error(y, y2_predict)
# Out[9]:
# 1.0987392142417856
plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()# 令degree=10
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)
y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
# Out[13]:
# 0.68726650324297611
plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()# 将横坐标均匀取值,查看100阶多项式回归拟合真正的曲线
# 如果degree太大,尽管均方误差较小,但是拟合出来的曲线可能完全不是我们想要的,称为过拟合
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, -1, 10])
plt.show()测试数据集的意义:
我们在训练模型时,是将模型不断的优化以对训练数据集分类结果最优,但却不能排除训练数据集的特殊性。于是测试数据集的意义便是涌来测试模型的“真正”性能,因为对于模型来说测试数据集是“全新”的。
train test split的意义(测试泛化能力)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
# Out[18]:
# 2.2199965269396573
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X_train, y_train)
y2_predict = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# Out[19]:
# 0.80356410562978997
# 虽然在面对训练数据集时均方误差较小,但是面对新的测试集时误差却变大了
poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X_train, y_train)
y10_predict = poly10_reg.predict(X_test)
mean_squared_error(y_test, y10_predict)
# Out[20]:
# 0.92129307221508061
# 误差非常大
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X_train, y_train)
y100_predict = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict)
# Out[21]:
# 14075796390.678177上面的绘图过程,实际是学习曲线:随着样本的逐渐增多,算法训练出的模型的表现能力。
04 学习曲线
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=10)
X_train.shape
# Out[5]:
# (75, 1)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
train_score = []
test_score = []
for i in range(1, 76):
lin_reg = LinearRegression()
lin_reg.fit(X_train[:i], y_train[:i])
# 分别计算模型预测训练数据与测试数据的均方误差
y_train_predict = lin_reg.predict(X_train[:i])
train_score.append(mean_squared_error(y_train[:i], y_train_predict))
y_test_predict = lin_reg.predict(X_test)
test_score.append(mean_squared_error(y_test, y_test_predict))
# 绘制均方根误差曲线
plt.plot([i for i in range(1, 76)], np.sqrt(train_score), label='train')
plt.plot([i for i in range(1, 76)], np.sqrt(test_score), label='test')
plt.legend()
plt.show()# 将上述方法进行封装
def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
train_score = []
test_score = []
for i in range(1, len(X_train)+1):
algo.fit(X_train[:i], y_train[:i])
# 分别计算模型预测训练数据与测试数据的均方误差
y_train_predict = lin_reg.predict(X_train[:i])
train_score.append(mean_squared_error(y_train[:i], y_train_predict))
y_test_predict = algo.predict(X_test)
test_score.append(mean_squared_error(y_test, y_test_predict))
plt.plot([i for i in range(1, len(X_train)+1)],
np.sqrt(train_score), label='train')
plt.plot([i for i in range(1, len(X_train)+1)],
np.sqrt(test_score), label='test')
plt.legend()
plt.axis([0, len(X_train)+1, 0, 4])
plt.show()
plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test) # 欠拟合from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
# 使用二阶多项式回归,稳定误差较低
poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)# 过拟合
poly30_reg = PolynomialRegression(degree=30)
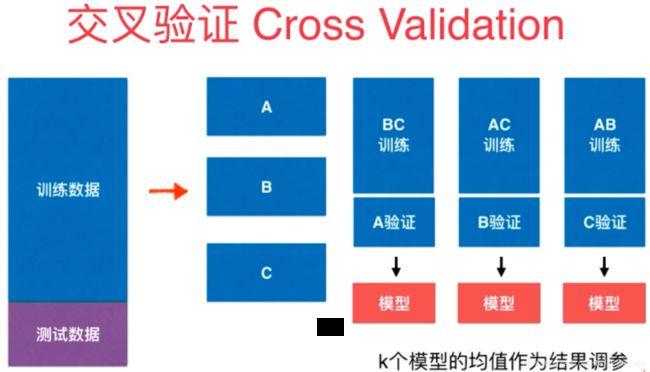
plot_learning_curve(poly30_reg, X_train, X_test, y_train, y_test)只将原来数据分为训练数据和测试数据其实还有缺点,训练数据负责训练模型,测试数据拿来调参,然而最好还有另外的数据集完成对模型的评测。
如果验证数据集中有比较极端的数据时仍然会导致模型的不准确。
解决办法:交叉验证
05 交叉验证
import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target测试train_test_split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4)
from sklearn.neighbors import KNeighborsClassifier
best_score, best_p , best_k = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights='distance', n_neighbors=k, p=p)
knn_clf.fit(X_train, y_train)
score = knn_clf.score(X_test, y_test)
if score > best_score:
best_score, best_p , best_k = score, p, k
print("Best K = ", best_k)
print("Best P = ", best_p)
print("Best Score = ", best_score)
"""
Best K = 10
Best P = 4
Best Score = 0.986091794159
"""
使用交叉验证
from sklearn.model_selection import cross_val_score
knn_clf = KNeighborsClassifier()
# 默认将X_train分成三份进行交叉验证
cross_val_score(knn_clf, X_train, y_train)
# Out[6]:
# array([ 0.98071625, 0.97771588, 0.96629213])
# 交叉验证找到的k和p更趋近于最优情况,因为可能训练的模型可能过拟合了train_test_split中分离出来的测试数据集
# 交叉验证过程中一般不会过拟合某一数据,所以分值可能小一点
best_score, best_p , best_k = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights='distance', n_neighbors=k, p=p)
scores = cross_val_score(knn_clf, X_train, y_train)
score = np.mean(scores)
if score > best_score:
best_score, best_p , best_k = score, p, k
print("Best K = ", best_k)
print("Best P = ", best_p)
print("Best Score = ", best_score)
"""
Best K = 3
Best P = 3
Best Score = 0.978655813903
"""
best_knn_clf = KNeighborsClassifier(weights='distance', n_neighbors=3, p=3)
best_knn_clf.fit(X_train, y_train)
best_knn_clf.score(X_test, y_test)
# Out[9]:
# 0.98470097357440889回顾网格搜索
from sklearn.model_selection import GridSearchCV
param_grid = [
{
'weights':['distance'],
'n_neighbors':[i for i in range(2, 11)],
'p':[i for i in range(1, 6)]
}
]
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)
Fitting 3 folds for each of 45 candidates, totalling 135 fits
[Parallel(n_jobs=1)]: Done 135 out of 135 | elapsed: 1.1min finished
"""
Out[10]:
GridSearchCV(cv=None, error_score='raise',
estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=10, p=5,
weights='distance'),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'weights': ['distance'], 'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=1)
"""
grid_search.best_score_
# Out[14]:
# 0.97866419294990725
grid_search.best_params_
# Out[12]:
# {'n_neighbors': 3, 'p': 3, 'weights': 'distance'}
best_knn_clf = grid_search.best_estimator_
best_knn_clf.score(X_test, y_test)
# Out[13]:
# 0.98470097357440889
# 指定交叉验证共分成几份
cross_val_score(knn_clf, X_train, y_train, cv=5)
# Out[15]:
# array([ 0.98181818, 0.99086758, 0.99069767, 0.95774648, 0.96682464])
# 网格搜索同上
GridSearchCV(knn_clf, param_grid, verbose=1, cv=5)
"""
Out[17]:
GridSearchCV(cv=5, error_score='raise',
estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=10, p=5,
weights='distance'),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'weights': ['distance'], 'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=1)
"""偏差方差平衡
下图打靶的例子可以很好地解释二者差别,偏差是偏离中心的程度,方差是在中心附近离散的程度。
模型误差 = 偏差(Bias) + 方差(Variance) + 不可避免的误差
有一些算法是天生的高方差的算法,例如kNN;
非参数学习通常都是高方差算法,因为我们不对数据进行任何假设;
有一些算天生的高偏差的算法,例如线性回归;
参数学习通常都是高偏差算法,因为对数据有很强的假设。
然而大多数算法具有相应的参数,可以调整偏差与方差,比如kNN中的k,线性回归中的多项式回归......
偏差和方差通常是矛盾的。机器学习的主要挑战来自于方差!
为此有以下解决高方差的手段:
1. 降低模型复杂度
2. 减少数据维度,(降噪)
3. 增加样本数
4. 使用验证集
5. 模型正则化
查看过拟合时的参数theta,可以发现有一些theta值特别大使得曲线特别的陡峭,为了解决这个问题就需要加入模型正则化。
需要注意的是theta0不需要加进去,因为它并不是某一个x的系数,而是一个截距。决定曲线的高低而不是曲线的陡峭程度。
"""
array([ 1.21097006e+12, 1.19194835e+01, 1.78867390e+02,
-2.95986877e+02, -1.79531574e+04, -1.54151055e+04,
8.34384008e+05, 8.19758496e+05, -2.23628081e+07,
-1.44767967e+07, 3.87211849e+08, 1.13415788e+08,
-4.61600837e+09, -1.25028833e+08, 3.93150842e+10,
-5.47613295e+09, -2.44176507e+11, 5.46306491e+10,
1.11421150e+12, -2.76412491e+11, -3.71329570e+12,
8.55468251e+11, 8.80961399e+12, -1.60750401e+12,
-1.39204217e+13, 1.49444135e+12, 1.19236839e+13,
2.47521688e+11, 4.42430553e+11, -1.64287100e+12,
-1.05153908e+13, -1.80895216e+11, 3.00207361e+12,
2.75578358e+12, 8.74123180e+12, -1.36695737e+12,
-1.22670880e+12, -7.00478229e+11, -8.24896132e+12,
-8.66309669e+11, -2.75689072e+12, 1.39629460e+12,
6.26144462e+12, -3.47974176e+11, 6.29124500e+12,
1.33767267e+12, -6.11898796e+11, 2.92306225e+11,
-6.59758602e+12, -1.85664319e+12, -4.13408892e+12,
-9.72006661e+11, -3.99038794e+11, -7.53680910e+11,
5.49213942e+12, 2.18520516e+12, 5.24342787e+12,
7.50245141e+11, 5.50263530e+11, 1.70648559e+12,
-2.26789352e+12, -1.84598222e+11, -5.47303676e+12,
-2.86220611e+12, -3.88076540e+12, -1.19593236e+12,
1.16313815e+12, -1.41081942e+12, 3.56349490e+12,
7.12345817e+11, 4.76398301e+12, 2.60002802e+12,
1.84224334e+12, 3.06318514e+12, -1.33316411e+12,
6.18515991e+11, -2.64566982e+12, -1.01426612e+12,
-4.76745537e+12, -3.59229268e+12, -1.68056493e+12,
-3.57479576e+12, 2.06628597e+12, -6.07535225e+11,
3.40447747e+12, 3.42181114e+12, 3.31401269e+12,
4.92289470e+12, 3.79997144e+11, 1.34187245e+12,
-3.34878935e+12, -2.07865993e+12, -3.24636729e+12,
-5.48901934e+12, 5.87221409e+11, -2.27318240e+12,
2.60029053e+12, 8.21819706e+12, 4.79214839e+10,
-3.11436331e+12, -6.27732007e+11])
"""上式通常称为 岭回归 Ridge Regression
06 岭回归
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
lin_reg = LinearRegression()
def PolynomialRegression(degree):
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", lin_reg)
])
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.metrics import mean_squared_error
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict)
# Out[6]:
# 167.94010867755134
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
# 将绘制模型预测曲线的方法封装起来
def plot_model(model):
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
plot_model(poly_reg)使用岭回归
from sklearn.linear_model import Ridge
# 封装岭回归的过程
def RidgeRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("ridge_reg", Ridge(alpha=alpha))
])
# 由于后面那一项是平方和的累加较大,我们可以将alpha取的小一点
ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)
y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
# Out[10]:
# 1.3233492753969822
# 与之前方法相比,曲线的平滑程度更好
plot_model(ridge1_reg)
ridge2_reg = RidgeRegression(20, 1)
ridge2_reg.fit(X_train, y_train)
y2_predict = ridge2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# Out[12]:
# 1.1888759304218468
plot_model(ridge2_reg)ridge3_reg = RidgeRegression(20, 100)
ridge3_reg.fit(X_train, y_train)
y3_predict = ridge3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)
# Out[14]:
# 1.3196456113086197
plot_model(ridge3_reg)# alpha过大则变成优化后面一项,使得所有的seita都为0
ridge4_reg = RidgeRegression(20, 10000000)
ridge4_reg.fit(X_train, y_train)
y4_predict = ridge4_reg.predict(X_test)
mean_squared_error(y_test, y4_predict)
# Out[16]:
# 1.8408455590998372
plot_model(ridge4_reg)在如何表达theta最小的问题上,选择另一种指标。
07 LASSO
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
lin_reg = LinearRegression()
def PolynomialRegression(degree):
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", lin_reg)
])
from sklearn.metrics import mean_squared_error
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict)
# Out[6]:
# 167.94010867755134
# 绘制模型对应的曲线
def plot_model(model):
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
plot_model(poly_reg)LASSO
from sklearn.linear_model import Lasso
def LassoRegression(degree, alpha):
# 传入每一步骤所对应的类 1.多项式的特征 2.数据归一化 3.线性回归
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lasso_reg", Lasso(alpha=alpha))
])
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)
y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
# Out[11]:
# 1.1496080843259968
plot_model(lasso1_reg)lasso2_reg = LassoRegression(20, 0.1)
lasso2_reg.fit(X_train, y_train)
y2_predict = lasso2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# Out[13]:
# 1.1213911351818648
plot_model(lasso2_reg)lasso3_reg = LassoRegression(20, 1)
lasso3_reg.fit(X_train, y_train)
y3_predict = lasso3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)
# Out[15]:
# 1.8408939659515595
plot_model(lasso3_reg)LASSO趋向于使得一部分theta值变为0.所以可作为特征选择用。
原因如下:
岭回归的梯度求出来和theta有关,是按theta的取值不断下降的。
LASSO的梯度求出来只能取1,-1或0所以只能使用规则的方式下降,在下降时使得某一特征的值变为0。
可以看到,弹性网结合了Ridge和LASSO的优点,但是时间复杂度较高。
最后,欢迎各位读者共同交流,祝好。