AVL tree

Defination

An empty binary tree is height balanced. If T is a nonempty binary tree with $T_L$ and $T_R$ as its left and right subtrees, then T is height balanced iff
(1) $T_L$ and $T_R$ are height balanced
(2) $|h_L-h_R|\le 1$ where $h_L$ and $h_R$ are the heights of $T_L$ and $T_R$ , respectively.

Insertion

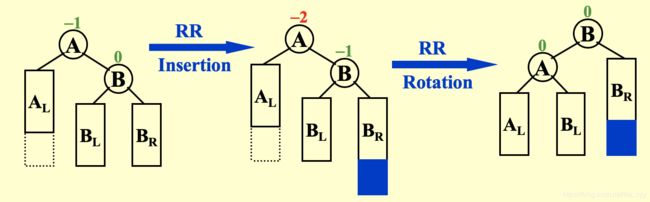
Case 1: RR

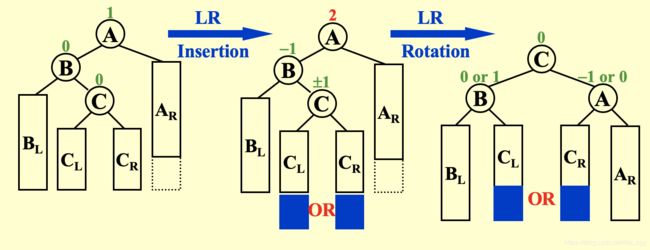
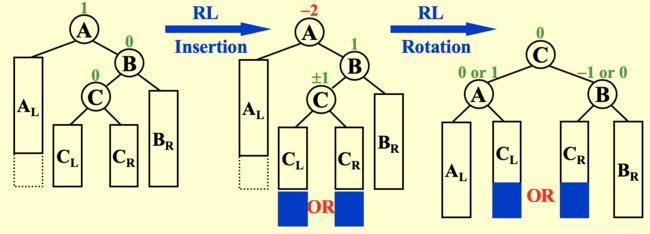
Case 2: LL

similar to RR

Case 3: LRCase 4: RL

Let $n_h$ be the minimum number of nodes in a height balanced tree of height h.

Then $n_h=n_{h-1}+n_{h-2}+1$

Fibonacci numbers:

$F_0=0,F_1=1,F_i=F_{i-1}+F_{i-2}$ , for $i>1$

$\Rightarrow$ $n_h=F_{h+2}-1$, for $h\ge 0$

$\Rightarrow$ h = O(ln n)​

性能评估

每次操作需要遍历从最底端到root的各个节点，时间复杂度为O(h)，调整操作时间复杂度为O(1)。故每次操作时间复杂度为O(h)。
又 h = O(lnN)
故操作时间复杂度为O(lnN)

exercises

$n_h=F_{h+2}-1=F_{7+2}-1=34-1=33$

references

https://blog.csdn.net/Woolseyyy/article/details/51505383

code

#ifndef _AVL_TREE_H_
#define _AVL_TREE_H_

typedef int Type;

typedef struct AVLTreeNode{
    Type key;                    // 关键字(键值)
    int height;
    struct AVLTreeNode *left;    // 左孩子
    struct AVLTreeNode *right;    // 右孩子
}Node, *AVLTree;

// 获取AVL树的高度
int avltree_height(AVLTree tree);

// 前序遍历"AVL树"
void preorder_avltree(AVLTree tree);
// 中序遍历"AVL树"
void inorder_avltree(AVLTree tree);
// 后序遍历"AVL树"
void postorder_avltree(AVLTree tree);

void print_avltree(AVLTree tree, Type key, int direction);

// (递归实现)查找"AVL树x"中键值为key的节点
Node* avltree_search(AVLTree x, Type key);
// (非递归实现)查找"AVL树x"中键值为key的节点
Node* iterative_avltree_search(AVLTree x, Type key);

// 查找最小结点：返回tree为根结点的AVL树的最小结点。
Node* avltree_minimum(AVLTree tree);
// 查找最大结点：返回tree为根结点的AVL树的最大结点。
Node* avltree_maximum(AVLTree tree);

// 将结点插入到AVL树中，返回根节点
Node* avltree_insert(AVLTree tree, Type key);

// 删除结点(key是节点值)，返回根节点
Node* avltree_delete(AVLTree tree, Type key);

// 销毁AVL树
void destroy_avltree(AVLTree tree);


#endif

/**
 * AVL树(C语言): C语言实现的AVL树。
 *
 * @author skywang
 * @date 2013/11/07
 */

#include 
#include 
#include "avltree.h"

#define HEIGHT(p)    ( (p==NULL) ? -1 : (((Node *)(p))->height) )
#define MAX(a, b)    ( (a) > (b) ? (a) : (b) )

/*
 * 获取AVL树的高度
 */
int avltree_height(AVLTree tree)
{
    return HEIGHT(tree);
}

/*
 * 前序遍历"AVL树"
 */
void preorder_avltree(AVLTree tree)
{
    if(tree != NULL)
    {
        printf("%d ", tree->key);
        preorder_avltree(tree->left);
        preorder_avltree(tree->right);
    }
}


/*
 * 中序遍历"AVL树"
 */
void inorder_avltree(AVLTree tree)
{
    if(tree != NULL)
    {
        inorder_avltree(tree->left);
        printf("%d ", tree->key);
        inorder_avltree(tree->right);
    }
}

/*
 * 后序遍历"AVL树"
 */
void postorder_avltree(AVLTree tree)
{
    if(tree != NULL)
    {
        postorder_avltree(tree->left);
        postorder_avltree(tree->right);
        printf("%d ", tree->key);
    }
}

/*
 * (递归实现)查找"AVL树x"中键值为key的节点
 */
Node* avltree_search(AVLTree x, Type key)
{
    if (x==NULL || x->key==key)
        return x;

    if (key < x->key)
        return avltree_search(x->left, key);
    else
        return avltree_search(x->right, key);
}

/*
 * (非递归实现)查找"AVL树x"中键值为key的节点
 */
Node* iterative_avltree_search(AVLTree x, Type key)
{
    while ((x!=NULL) && (x->key!=key))
    {
        if (key < x->key)
            x = x->left;
        else
            x = x->right;
    }

    return x;
}

/* 
 * 查找最小结点：返回tree为根结点的AVL树的最小结点。
 */
Node* avltree_minimum(AVLTree tree)
{
    if (tree == NULL)
        return NULL;

    while(tree->left != NULL)
        tree = tree->left;
    return tree;
}
 
/* 
 * 查找最大结点：返回tree为根结点的AVL树的最大结点。
 */
Node* avltree_maximum(AVLTree tree)
{
    if (tree == NULL)
        return NULL;

    while(tree->right != NULL)
        tree = tree->right;
    return tree;
}

/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* left_left_rotation(AVLTree k2)
{
    AVLTree k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = MAX( HEIGHT(k2->left), HEIGHT(k2->right)) + 1;
    k1->height = MAX( HEIGHT(k1->left), k2->height) + 1;

    return k1;
}

/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* right_right_rotation(AVLTree k1)
{
    AVLTree k2;

    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = MAX( HEIGHT(k1->left), HEIGHT(k1->right)) + 1;
    k2->height = MAX( HEIGHT(k2->right), k1->height) + 1;

    return k2;
}

/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* left_right_rotation(AVLTree k3)
{
    k3->left = right_right_rotation(k3->left);

    return left_left_rotation(k3);
}

/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* right_left_rotation(AVLTree k1)
{
    k1->right = left_left_rotation(k1->right);

    return right_right_rotation(k1);
}

/*
 * 创建AVL树结点。
 *
 * 参数说明：
 *     key 是键值。
 *     left 是左孩子。
 *     right 是右孩子。
 */
static Node* avltree_create_node(Type key, Node *left, Node* right)
{
    Node* p;

    if ((p = (Node *)malloc(sizeof(Node))) == NULL)
        return NULL;
    p->key = key;
    p->height = 0;
    p->left = left;
    p->right = right;

    return p;
}

/* 
 * 将结点插入到AVL树中，并返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
Node* avltree_insert(AVLTree tree, Type key)
{
    if (tree == NULL) 
    {
        // 新建节点
        tree = avltree_create_node(key, NULL, NULL);
        if (tree==NULL)
        {
            printf("ERROR: create avltree node failed!\n");
            return NULL;
        }
    }
    else if (key < tree->key) // 应该将key插入到"tree的左子树"的情况
    {
        tree->left = avltree_insert(tree->left, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2)
        {
            if (key < tree->left->key)
                tree = left_left_rotation(tree);
            else
                tree = left_right_rotation(tree);
        }
    }
    else if (key > tree->key) // 应该将key插入到"tree的右子树"的情况
    {
        tree->right = avltree_insert(tree->right, key);
        // 插入节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2)
        {
            if (key > tree->right->key)
                tree = right_right_rotation(tree);
            else
                tree = right_left_rotation(tree);
        }
    }
    else //key == tree->key)
    {
        printf("添加失败：不允许添加相同的节点！\n");
    }

    tree->height = MAX( HEIGHT(tree->left), HEIGHT(tree->right)) + 1;

    return tree;
}

/* 
 * 删除结点(z)，返回根节点
 *
 * 参数说明：
 *     ptree AVL树的根结点
 *     z 待删除的结点
 * 返回值：
 *     根节点
 */
static Node* delete_node(AVLTree tree, Node *z)
{
    // 根为空 或者 没有要删除的节点，直接返回NULL。
    if (tree==NULL || z==NULL)
        return NULL;

    if (z->key < tree->key)        // 待删除的节点在"tree的左子树"中
    {
        tree->left = delete_node(tree->left, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2)
        {
            Node *r =  tree->right;
            if (HEIGHT(r->left) > HEIGHT(r->right))
                tree = right_left_rotation(tree);
            else
                tree = right_right_rotation(tree);
        }
    }
    else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
    {
        tree->right = delete_node(tree->right, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2)
        {
            Node *l =  tree->left;
            if (HEIGHT(l->right) > HEIGHT(l->left))
                tree = left_right_rotation(tree);
            else
                tree = left_left_rotation(tree);
        }
    }
    else    // tree是对应要删除的节点。
    {
        // tree的左右孩子都非空
        if ((tree->left) && (tree->right))
        {
            if (HEIGHT(tree->left) > HEIGHT(tree->right))
            {
                // 如果tree的左子树比右子树高；
                // 则(01)找出tree的左子树中的最大节点
                //   (02)将该最大节点的值赋值给tree。
                //   (03)删除该最大节点。
                // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                Node *max = avltree_maximum(tree->left);
                tree->key = max->key;
                tree->left = delete_node(tree->left, max);
            }
            else
            {
                // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                // 则(01)找出tree的右子树中的最小节点
                //   (02)将该最小节点的值赋值给tree。
                //   (03)删除该最小节点。
                // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                Node *min = avltree_maximum(tree->right);
                tree->key = min->key;
                tree->right = delete_node(tree->right, min);
            }
        }
        else
        {
            Node *tmp = tree;
            tree = tree->left ? tree->left : tree->right;
            free(tmp);
        }
    }

    return tree;
}

/* 
 * 删除结点(key是节点值)，返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 待删除的结点的键值
 * 返回值：
 *     根节点
 */
Node* avltree_delete(AVLTree tree, Type key)
{
    Node *z; 

    if ((z = avltree_search(tree, key)) != NULL)
        tree = delete_node(tree, z);
    return tree;
}

/* 
 * 销毁AVL树
 */
void destroy_avltree(AVLTree tree)
{
    if (tree==NULL)
        return ;

    if (tree->left != NULL)
        destroy_avltree(tree->left);
    if (tree->right != NULL)
        destroy_avltree(tree->right);

    free(tree);
}

/*
 * 打印"AVL树"
 *
 * tree       -- AVL树的节点
 * key        -- 节点的键值 
 * direction  --  0，表示该节点是根节点;
 *               -1，表示该节点是它的父结点的左孩子;
 *                1，表示该节点是它的父结点的右孩子。
 */
void print_avltree(AVLTree tree, Type key, int direction)
{
    if(tree != NULL)
    {
        if(direction==0)    // tree是根节点
            printf("%2d is root\n", tree->key, key);
        else                // tree是分支节点
            printf("%2d is %2d's %6s child\n", tree->key, key, direction==1?"right" : "left");

        print_avltree(tree->left, tree->key, -1);
        print_avltree(tree->right,tree->key,  1);
    }
}