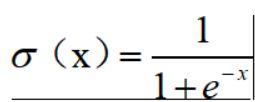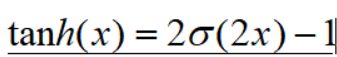简单的多层全连接前向网络 ——深度学习入门之PyTorch
目录
1.模拟神经元
2.单层神经网络的分类器
3.激活函数
4.神经网络的结构
为什么要使用激活函数?
5.模型的表示能力与容量
1.模拟神经元
神经网络最开始是受到了模拟脑神经元的启发。
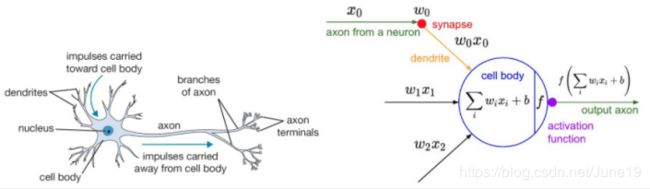
图1 脑神经元与神经网络的相似之处
脑中的一个计算单元是一个简单的脑神经元。
脑神经元受到一个输入的信号,通过不同的突触,信号进入神经元,接着通过神经元内部的激活处理,最后沿着神经元的轴突产生一个输出信号,这个轴突通过下一个神经元的突触相连将输出信号传到下一个神经元。
在神经网络的计算模型中,输入信号就是输入数据,模型的参数就是突触,然后输入信号传入神经元就像是输入数据和模型参数进行线性组合,然后经过激活函数,最后传出模型。
模型参数通过学习可以控制输入数据传入神经元的强度,激活函数就是神经元内部的激活处理,最后将结果输出变成第二层网络的输入。
2.单层神经网络的分类器
由于激活函数的作用,所以我们可以将一层神经网络用做分类器,正样本就让激活函数激活变大,负样本就让激活函数激活变小。
e.g. 使用sigmoid 激活函数做一个二分类问题。
3.激活函数
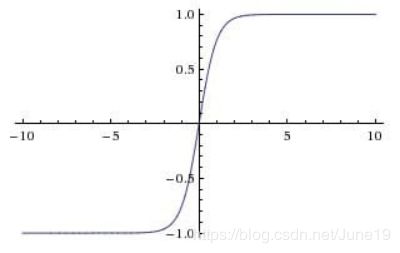
- Sigmoid
数学表达式:
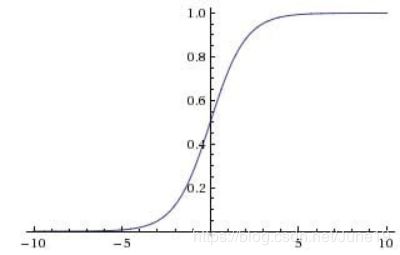
Sigmoid是将一个实数输入转化到 0 - 1 之间的输出。
也就是将越大的负数转化到越靠近0,越大的正数转化到越靠近1.
Sigmoid函数的缺点:
- Sigmoid函数会造成梯度消失。
- Sigmoid输出不是以0为均值,这就会导致经过sigmoid激活函数之后的输出,作为后面一层网络的输入的时候是非0均值的,这时如果输入进入下一层神经元的时候全是正的,这就会导致梯度全都是正的,那么参数更新的时候永远都是正梯度。
2.Tanh
Tanh函数是sigmoid函数的变形,其数学表达式为
输入数据转化到 -1 - 1 之间,输出变成了0均值,在一定程度上解决了sigmoid函数的第二个问题,但仍然存在梯度消失的问题。
因此,tanh函数总是比sigmoid函数更好。
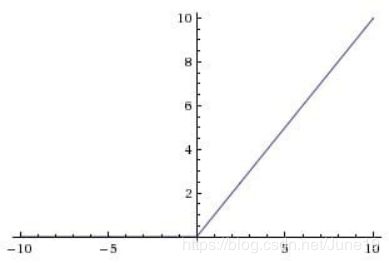
3.ReLU
ReLU激活函数(Rectified Linear Unit)近几年越来越流行。
其数学表示式为:f(x) = max(0, x)
这个激活函数只是将大于0的部分保留,将小于0的部分变成0.
ReLU函数优点:
- 相比于sigmoid函数和tanh函数,relu函数能够极大地加速随机梯度下降法的收敛速度,这是因为它是线性的,且不存在梯度消失的问题。
- 相比于sigmoid函数和tanh函数的复杂计算而言,relu函数的计算方法更加简单,只需要一个阈值过滤就可以得到结果,不需要复杂的运算。
ReLU函数缺点:
训练的时候很脆弱,如果一个很大的梯度经过relu函数,更新参数之后,会使得这个神经元不会对任何数据有激活现象。因为relu函数本质是一个不可逆的过程,它会直接去掉输入小于0的部分,在实际操作中可以通过设置比较小的学习率来避免这个小问题。
4.Leaky ReLU
Leaky ReLU函数是relu函数的变式,主要是为了修复relu函数中训练比较弱的这个缺点,不将x < 0 的部分变成0,而是给它一个很小的负的斜率。比如0.01.
其数学表示式为: f(x) = I(x < 0)(ax) + I(x > = 0)(x)
其中a是一个很小的常数,这样就可以使得输入小于0的时候也有一个小的梯度。
5.Maxout
Maxout既有着relu函数的优点,同时也避免了relu函数训练脆弱的缺点。不过它本身也有一个缺点,就是它加倍了模型的参数,导致模型的存储变大。
总结:
实际中用得较多的还是ReLU函数,但是注意学习率的设定不要太大,一定不要使用sigmoid函数,可以试一下tanh函数,但是一般它的效果都比Relu 和maxout差。最后,在实际应用中很少使用混合类型的激活函数,也就是说一般在同一个网络中我们使用同一类型的激活函数。
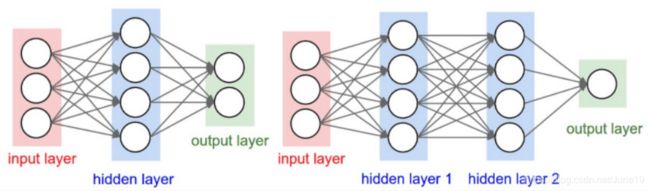
4.神经网络的结构
神经网络就是很多个神经元堆在一起形成一层神经网络,那么多个层堆叠在一起就是深层神经网络,我们可以通过下面的图展示一个两层的神经网络和三层的神经网络。
可以看到,神经网络的结构其实非常简单,主要有输入层,隐藏层,输出层构成,输入层需要根据特征数目来决定,输出层根据解决的问题来决定,那么隐藏层的网路层数以及每层的神经元数就是可以调节的参数,而不同的层数和每层的参数对模型的影响非常大。
Demo:https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
神经网络向前传播也非常简单,就是一层一层不断做运算就可以了,可以看看下面这个例子:
为什么要使用激活函数?
激活函数在神经网络中非常重要,使用激活函数也是非常必要的,前面我们从人脑神经元的角度理解了激活函数,因为神经元需要通过激活才能往后传播,所以神经网络中需要激活函数,下面我们从数学的角度理解一下激活函数的必要性。
比如一个两层的神经网络,使用 A 表示激活函数,那么
y=w2A(w1x)y=w2A(w1x)
如果我们不使用激活函数,那么神经网络的结果就是
y=w2(w1x)=(w2w1)x=w¯xy=w2(w1x)=(w2w1)x=w¯x
可以看到,我们将两层神经网络的参数合在一起,用 w¯w¯ 来表示,两层的神经网络其实就变成了一层神经网络,只不过参数变成了新的 w¯w¯,所以如果不使用激活函数,那么不管多少层的神经网络,y=wn⋯w2w1x=w¯xy=wn⋯w2w1x=w¯x,就都变成了单层神经网络,所以在每一层我们都必须使用激活函数。
5.模型的表示能力与容量
若数据不太复杂,那么容量小的模型反而有更好的效果。但如何去衡量到底多小才算是小模型呢?其次,小的模型在使用如梯度下降法等训练的时候通常更难。因为神经网络的损失函数一般是非凹的,容量小的网络更容易陷入局部极小点而达不到最优的效果,同时这些局部最小点的方差特别大。所以建议使用大容量的网络去训练模型,同时运用一些方法来控制网络的过拟合,这些方法在后面再进行详细介绍。