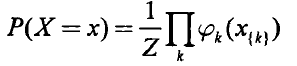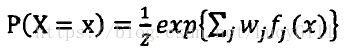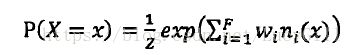马尔可夫逻辑网终极理解
最近在学习马尔科夫逻辑网相关知识,查阅相关资料无数,仍然觉得无法掌握其中内涵。历时约2周,终于在今天对其内涵了解一二,特此记录自己的理解。
觉得不错的马尔科夫逻辑网相关资料:
1.读懂概率图模型:你需要从基本概念和参数估计开始
https://blog.csdn.net/lucygill/article/details/79734874https://blog.csdn.net/lucygill/article/details/79734874
2. 数据挖掘|概率图模型(一)
https://zhuanlan.zhihu.com/p/22751416
3. 马尔科夫逻辑网原始论文的翻译
https://www.cnblogs.com/limitplus/archive/2010/03/05/1679451.html
4. 有实例的一个ppt
https://max.book118.com/html/2017/0704/120299628.shtm
下面说一下自己的理解。
一. 准备知识
如果想理解马尔科夫逻辑网,需要有:
1. 概率图模型相关知识
所谓概率图模型,就是以图的形式来研究概率的一种方式。在图中,每个节点表示一个随机变量,每条边表示随机变量之间的关系。概率图模型又分为两种:贝叶斯网络和马尔科夫网络。贝叶斯网络即表示概率及其之间关系的有向图,马尔科夫网络即表示概率及其之间关系的无向图。
贝叶斯网络在我看来,只是条件概率的另一种表现形式。马尔科夫网络相对复杂,它对图中每一个团(相互之间都有连边的节点称为“团”)都定义了一个势函数(potential function),表示的是当确定每个节点的取值时,该团的可信度。其概率公式如下:
其中Z为归一化函数,是一个常数。x{k}是第k个团中包含的所有节点的取值。
把势函数定义为指数函数,公式可改为:
其中,wj为团j的权重,fj(x)为团j的特征函数。
2. 一阶谓词逻辑的简单认识
一阶谓词逻辑在离散数学里有详细的介绍。马尔科夫逻辑网中用到的是把规则转化成子句的集合。如:P->Q <=> ~PvQ。也就是P=0或Q=1
二. 马尔科夫逻辑网
马尔科夫逻辑网把一阶谓词逻辑和马尔科夫网络结合起来。一阶谓词逻辑本身可以进行推理,但这种推理过于严谨。在它的认知中,一件事非错即对,无可商量。而马尔科夫逻辑网将这种硬性约束转化为软性约束,给出一件事为真的概率而非直接判断它的对错。
马尔科夫逻辑网的构建过程主要分为以下几步:
1. 将每条规则转化为子句的集合
2. 每个子句作为一个节点,每个集合中的子句相互之间都有连边,构成马尔科夫逻辑网
马尔科夫逻辑网的概率计算公式如下:
其中,ni(x)表示规则Fi的取值为真的对应闭规则的个数。
这里,特征函数是ni(x)。势函是exp(wi*ni(x)),表示第i个团(规则)的可信程度。规则的权重越大,满足规则的闭规则个数越多,说明当前取值x在这个规则下越可信。把当前取值在所有规则下的可信度相乘,再除以归一化因子,就能得到当前取值的概率。在推理过程中,选择使概率最大的一组取值作为推理结果。
势函数的另一种解释:exp(wi*ni(x))可以看作exp(wi)*exp(wi)*...*exp(wi)(ni(x)个)。也就是说,每个团都有自己的势函数exp(wi),给每个规则定义相同的势函数。如果规则相同,不管规则内填充的常数是什么,势函数都相同。事实上,每个团肯定能匹配到一个规则,因为团就是由规则化来的(见下表一阶谓词逻辑和马尔科夫逻辑网 的对应关系)。这样我们就能直观解释上面的公式了:公式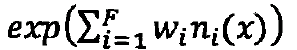 表达的仍然是每个团的势的乘积。首先遍历每个团,找到与之匹配的规则,将exp(wi)作为它的势。最后再把所有的势乘起来。
表达的仍然是每个团的势的乘积。首先遍历每个团,找到与之匹配的规则,将exp(wi)作为它的势。最后再把所有的势乘起来。
三. 马尔科夫逻辑网和一阶谓词逻辑的关系
事实上,马尔科夫逻辑网就是一阶谓词的“软化”。它把一阶谓词中非黑即白的判断转化成有概率的判断。通过把一阶谓词逻辑映射到马尔科夫网络上,它成功实现了概率化。当然,马尔科夫网络和一阶谓词逻辑有着对应关系。马尔科夫逻辑网做的工作事实上就是把一阶谓词逻辑映射到马尔科夫网络上。
一阶谓词逻辑:规则由谓词和连接词组成,若干条规则构建出一个世界。
马尔科夫逻辑网:团由节点和边组成,若干个团耦合在一起构成一个马尔科夫逻辑网。
对应关系展示如下表:
| 一阶谓词逻辑 | 规则 | 谓词 | 连接词 | 世界 |
| 马尔科夫逻辑网 | 团 | 节点 | 边 | 无向图 |