The Stein-Lov´asz Theorem 定理

The Stein-Lov´asz Theorem 定理及应用

The Stein-lov´asz定理最早由数学家[Stein(1974)][1]和[Lov´asz (1975)][2]提出。其最理论基础经过发展，应用到了[编码理论][3]。
The stein-lov´asz Theorem 理论最基本的模型是解决集合的元素覆盖问题。使用贪心算法，以获得一个使用最少列元完成最大行覆盖的方案。下面给出简单的Stein-Lovasm定理简单证明过程。在台湾作者李光祥的研究下，将原有的至少有1个 ′1′ 的行元升级到了至少又t个 ′1′ 的行元问题[Guang-Siang Lee][5]。
并且就[Deng’s article][4]的理解，介绍了一种分离哈希函数（Separating Hash Families）的应用，本文就分离函数族结合Stein-Lovasm的证明方法重新复述，并且认为其中具有冗余的证明部分，提出了自己的解释。

定理描述

• 原问题
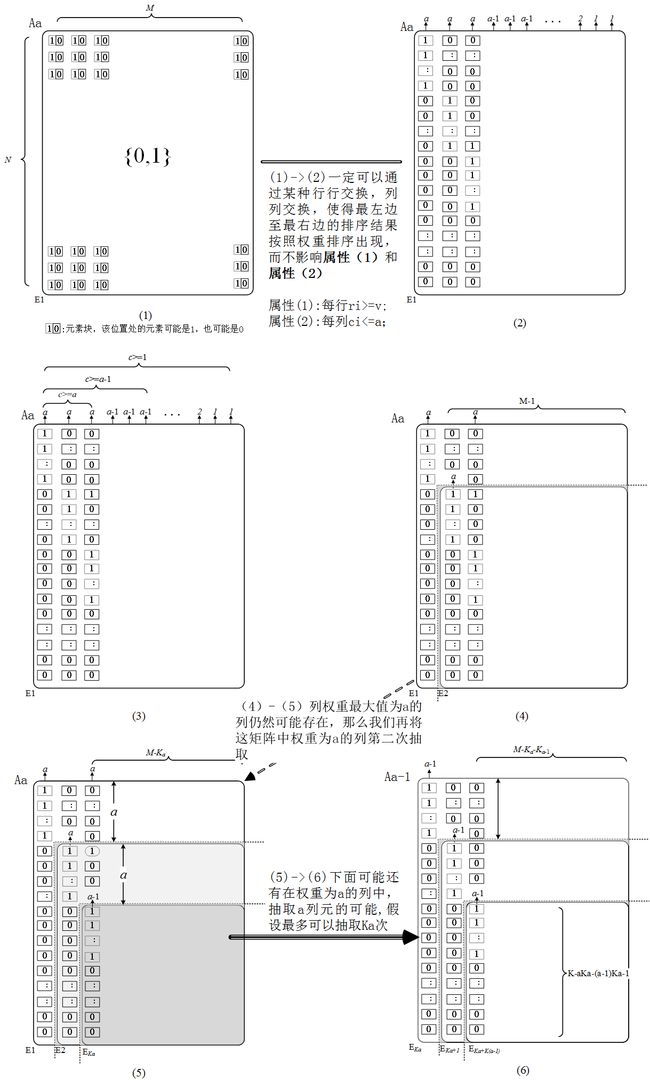
  假设 (0,1) 矩阵A的大小是 N×M ,矩阵 A 的特征是每行至少具有v个1，每列最多a个1。假设现在从其中抽取一个子矩阵 C⊂A ,大小是 N×K ，使得子矩阵的每行元素都不是全零行，证明 K 存在一个上界。
  
  K≤N/a+(M/v)ln(a)≤(M/v)(1+ln(a))
  
  原问题分析：能不能使用一种抽取列数尽可能少的方案，如果使用的列数目比给定的边界条件 N/a+(M/v)ln(a) 小，那么原来的问题就自然获得证明。

贪心算法

• 思路描述如下

  1. 初始化矩阵 (0,1) 矩阵 A ，每列的 ′1′ 权重值 ci∈{1,2,3,......,a} ,然后按照列权重按照a,a-1,a-2,…,1执行降序排序，此时的矩阵命名为 Aa ;
  2. 从最左边权重最高为a的第一列开始，删除这一列，并且这列对应的 ′1′ 所在相应的a个行也统一删掉。在删除1列和a行后的矩阵 A ，重新划定权重，继续寻找左边最高权重为a的列，继续删除。在删除 2 列和 2∗a 行后的矩阵 A ，重新划定权重，继续寻找左边最高权重为a的列，继续删除。重复 Ka 次后，把最高权重为a的列及对应的 a∗Ka 行都删掉了，此时的矩阵变成了 Aa−1 ;
  3. 以矩阵 Aa−1 开始，从左边权重最高为a-1的第一列开始，删除这一列，并且这列所对应的 a−1 行也统一删掉。删完后，重新划定权重，继续寻找左边最高权重为a-1的列，继续删除。重复 Ka−1 次后，把最高权重为a-1的列及其对应的 (a−1)∗Ka−1 行都删掉了，此时的矩阵变成了 Aa−2 .
  4. 重复步骤3，删除权重为a-2,a-3,…,1的列，直到矩阵 A1 变成了空。
  5. 将之前删除的所有列元集中起来重新组合成 N×K 矩阵， K=∑i:1→aKi

贪心算法的图例解释如附图1.

证明过程

按照贪心算法的步骤：
定义 Aa:=A ,其具有属性 (1) 、 (2) ：

(1) 每行至少有v个1;
(2) 每列至多有a个1;

将 Aa 分成两部分 A⋅a 与 Aa−1 ,其中 A⋅a 将所有每列的列权重都是a，而且pairwise disjoint(集合相交为0）的集合合并在一起，并且 A⋅a 的列元数目是 Ka ,删除 A⋅a 及其 ′1′ 所在的行后，剩下的 Aa−1 行数目为 ka−1=N−a∗Ka ,列数目为 M−Ka 。在 Aa−1 中，每列元的最大权重自然变成了a-1，而且每行权重至少是v不变（但凡是对权重有影响的列删除操作，都已经将其行也删除过了，而对这些剩下的行元没有丝毫影响）。所以 Aa−1 的属性变成了:

(3) 每行至少有v个1;
(4) 每列至多有a-1个1;

按照同样的方法，把 Aa−1 剔除权重为a-1并且pairwise disjoint的列元，以及其所在的 ′1′ 行元。那么剔除的列数为 Ka−1 ,得到结果 Aa−2 的行数是 ka−2=N−a∗Ka−(a−1)∗Ka−1 ，列数是 M−Ka−Ka−1 .
在最多a步的有限步骤下， Aa→Aa−1→Aa−2→...→A1→A0 , A0 为空时，贪婪算法的删除操作可以终止。注意到，将这些删除的列元具有的特征就刚好是每行权重至少有个1，即不是非零行，将他们集中起来，就可以得到所需的列数目 K ,并且肯定可以构成行数为 N (如果不是 N ,而是一个比 N 小的数 n ,那么最后一步剩下的 A0 行数是 N−n(>0) ，考虑到在删除时候属性 (1)(3)(5) 每行至少v个 ′1′ 的属性不变，所以 A0 中的列元素最小权重必然大于等于1，与 A0 的 ′0′ 含义相矛盾).

(5) 每行至少有v个1;
(6) 每列至多有0个1;

列数目 K 为:

K=Σi:1→aKi

当找到最佳的表达式后，下面寻找开始这其中每个 Ki 应该满足的条件,对于第一次的剔除操作完了后:

ka−1=N−a∗Ka

对于第二次的的剔除操作完了后:

ka−2=N−a∗Ka−(a−1)∗Ka−1=ka−1−(a−1)∗Ka−1.

所以，可以得到 Ki=(ki−ki−1)i.(ka=N)

另一方面，考虑到 (1)(2)(3)(4) 的属性，
在变化 Aa→Aa−1→Aa−2→...→A1→A0 时，
行变化： ka→ka−1→ka−2→...→ki→...→k1→k0 .每行至少又v个1,所以 v∗ki<=Si 。 Si 是总的权重;
列变化： M→M−Ka→M−Ka−Ka−1→...→M−Ka−...−Ki+1→...→M−Ka−...−K2→M−Ka−...−K1
每列至多 i 个1. S<=i(M−Ka...−Ki)<=iM .
所以: v∗ki<=iM⇒ki/i<=M/v
K=Σi:1→aKi=K=Σi:1→a(ki−ki−1i)=ka−ka−1a+ka−1−ka−2a−1+...+k2−k12+k1+k0
=kaa+ka−1a(a−1)+ka−2(a−1)(a−2)+......+k2−k12+k1−k0
≤Na+Mv(1a+1a−1+......+12)−k0
≤Na+Mvln(a)≤Mv(1+ln(a))

应用:证明分离哈希族的函数数目

原问题[4]：定义 (n,m,w1,w2)− separating hash family是一系列哈希函数 f 的集合 F 。其中每个函数完成映射： f:Y→X ，其中 |Y|=n , |X|=m 。对于输入集合 Y={1,2,3,4,...n} 的任意两个不相交子集 C1 、 C2 ， C1∩C2=ø ， |C1|=w1 , |C2|=w2 ，存在至少一个 f∈F 映射函数，使得函数值不相交：

{f(y):y∈C1}∩{f(y):y∈C2}=ø.

记 SHF(N;n,m,{w1,w2}) 来表示分离哈希函数族，其中 N 为哈希函数集合 F 的大小 |F|=N .

分析：将函数的输入输出关系记作如下图所示的方格点A(f,y)，其中第1列对应于输入集合 Y 中的输入值1，第二列对应输入值2，第三列…，共计 |Y|=n 种输入。第1行对应于第1个映射函数 f1∈F ，第2行对应于第2个映射函数 f2 ，共计有 |F|=N 种函数。

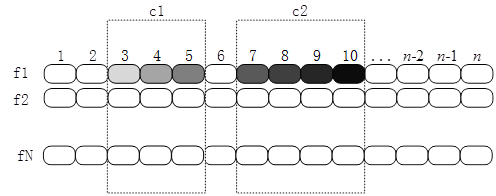
用图论的观点来解释 C1 与 C2 应该满足的要求。
C1∩C2=ø ,表示 w1 个点和 w2 个点都不相交，对应于图 G=(V,E) 中 w1+w2 个顶点数目，记 V=V1+V2 ， |V1|=w1 ， |V2|=w2 ， V1∩V2=ø ;
{f(y):y∈C1}∩{f(y):y∈C2}=ø 。对每1个函数映射值而言， A(f,y)∈{1,2,3,...,m} ,因此最多可能有 m 种不同的映射值，原来条件的 f(C1) , f(C2) 相交为空集，即映射值为空集。现在定义不同的映射值对应于不同的颜色，那么每个顶点的颜色数目最多可能有 m 种。先固定顶点集合 V2 ,观察 V1 中的点x,由于 A(f,V1)∩A(f,V2)=ø ，所以 A(f,x)∉A(f,V2) ，即 x 的顶点颜色与 V2 中每个顶点的颜色都不同。接下来，对 V1 中剩下的其他点也要满足同样的要求。那么，对于集合 V1 , V2 中所有顶点不能着与对方相同颜色的顶点关系用边来连接，最终可以连接成一个完全二分图 K(w1,w2) 每条边的两个顶点都具有不同的颜色值。

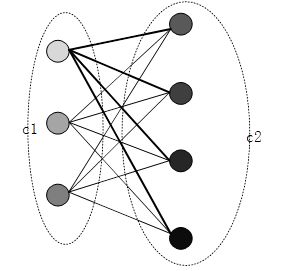
现在 C1 与 C2 应该满足的关系转化为了：提供m种不同颜色作为选择，保证二分图 Kw1,w2 中的任意两条边的顶点颜色都不相同。着色方案问题，不是研究重点，因此简记着色方案数目为 Π(Kw1,w2,m) .

原来的证明思路[4]：
我们首先构造一个关联矩阵 A ,列数为 mn ,对应所有顶点都着上 m 种可能的映射值。行数为 (n−w1w2) 对应所有满足子集长度要求的分离对集合编号总数。对于 w1 大小的子集，和不相交的 w2 子集，我们可以给行构建一个双计数变量： i1,i2 ，其中 i1∈{1,2,3,...,(nw1)} , i2∈{1,2,3,...,(n−w1w2)}
如果 ai,j=1 ,那么第 j 种函数映射值可以使得第 i1 个 w1 子集和第 i2 个 w2 子集不存在元素相交。否则 ai,j=0 。
现在考虑怎么使用现有的 A 中的列元（一个j列对应了某一种映射方案，也就是特定的一种映射方案函数f，如果需要 N 列的话，那么将需要使用N种函数）来对所有的任意 w1 , w2 可能子集都予以覆盖。那么这个问题的方向看起来就和Stein-Lov´asz定理一样——最坏情况的列元选取方案是多少种？选取映射方案的最坏上限值不超过多少，才能符合所有行元被最佳最少列cover掉的这个目标？
在文章[4]给出的一个上界是

N≤mw1+w2Π(Kw1,w2,m)(1+log(Cw1nCw2n−w1))

但其实个人认为不是这样，而是强行使用Stein-Lovasm定理。

解释：现在A中的每个元素 ai,j 是 (0,1) 矩阵，每行拥有的权重为 mn−w1−w2Π(Kw1,w2,m) ,每列至多拥有 Cw1nCw2n−w1 权重。按照Stein-Lov´asz定理，可得到 N 的上述边界。但是从证明过程的角度分析， A中的行数目也刚好是 Cw1nCw2n−w1 ，因此将这个最大权重的列选出，则可以作为一个子矩阵，cover掉所有的 Cw1nCw2n−w1 行。因此，N=1，而求解这个问题的上界 mw1+w2Π(Kw1,w2,m)(1+log(Cw1nCw2n−w1)) 已经在1的基础上放大了很多倍数，作了没必要的放大。从物理意义解释说，所选取的这个最大权重列，对于任意的 w1 ， w2 大小的子集，全部可以完成分离函数的映射条件。

[1]: S. K. Stein, Two combinatorial covering problems, J.Combinatorial Theory, Ser. A, 16 (1974), 391-397.
[2]: L. Lov´asz. On the ratio of optimal integral and fractional covers, Discrete Mathematics, 13 (1975), 383-390.
[3]: G. Cohen, S. Litsyn and G. Z´emor, On greedy algorithms in coding theory, IEEE Transactions on Information Theory, Vol. 42 no.6 (1996), 2053-2057
[4]: Dameng Deng, and Yuan Zhang, The Stein-Lov´asz Theorem and Its Applications to
Some Combinatorial arrays, JCMCC-Journal of Combinatorial Mathematicsand Combinatorial Computing, Vol.77 no.17 (2011).
[5]: Lee G S. An extension of Stein-Lovász theorem and some of its applications[J]. Journal of Combinatorial Optimization, 2013, 25(1): 1-18.

---

附图1