【学习笔记】主席树

1、前置知识

线段树、权值线段树、前缀和思想等

2、引入

主席树模板题

约定：
后面将第k小/大说成$kth$

解决什么问题：
给定一段区间，静态求区间$kth$

想想方法：

• 暴力：对于每一个询问，排个序，就行了，时间复杂度$O(nmlogn)$
• 莫队+树状数组：树状数组可以求给定区间$kth$，使用二分+树状数组，具体不展开，但是多个区间的话，需要不断地进行树状数组的add/del操作，那么使用莫队来优化区间端点的移动问题，时间复杂度$O((n+m)\sqrt{n}logn)$，莫队复杂度*树状数组复杂度
• 莫队+平衡树：把树状数组的部分替换成二叉查找树，用splay的一部分操作，需要用到kth操作，不用翻转标记什么的，时间复杂度$O((n+m)\sqrt{n}logn)$，跟上面的一样

目前想想，也就这三种方法，各有优劣，暴力时间复杂度不行，但是可以在线
后面两种因为莫队的原因必须离线

但是这三种方法时间都太慢，这个题目我们需要一个$O(nlogn)$的做法

于是主席树就诞生了

3、思想的推进

思考优化策略

一列数，可以对于每个点i都建一棵权值线段树，维护1~i这些数，每个不同的数出现的个数（权值线段树以值域作为区间）

现在，n棵线段树就建出来了，第i棵线段树代表1~i这个区间

例如，一列数，n为6，数分别为1 3 2 3 6 1
首先，每棵树都是这样的：

以第4棵线段树为例，1~4的数分别为1 3 2 3

因为是同一个问题，n棵权值线段树的形状是一模一样的，只有节点的权值不一样
所以这样的两棵线段树之间是可以相加减的（两颗线段树相减就是每个节点对应相减）

想想，第x棵线段树减去第y棵线段树会发生什么？
第x棵线段树代表的区间是[1,x]
第y棵线段树代表的区间是[1,y]
两棵线段树一减
设x>y，$[1,x]-[1,y]=[y+1,x]$
所以这两棵线段树相减可以产生一个新的区间对应的线段树！

等等，这不是前缀和的思想吗
这样一来，任意一个区间的线段树，都可以由我这n个基础区间表示出来了！
因为每个区间都有一个线段树
然后询问对应区间，在区间对应的线段树中查找kth就行了

这就是主席树的一个核心思想：前缀和思想

具体做法待会儿再讲，现在还有一个严峻的问题，就是n棵线段树空间太大了！
如何优化空间，就是主席树另一个核心思想

我们发现这n棵线段树中，有很多重复的点，这些重复的点浪费了大部分的空间，所以考虑如何去掉这些冗余点

在建树中优化

假设现在有一棵线段树，序列往右移一位，建一棵新的线段树
对于一个儿子的值域区间，如果权值有变化，那么新建一个节点，否则，连到原来的那个节点上

现在举几个例子来说明
序列4 3 2 3 6 1

区间[1,1]的线段树（蓝色节点为新节点）

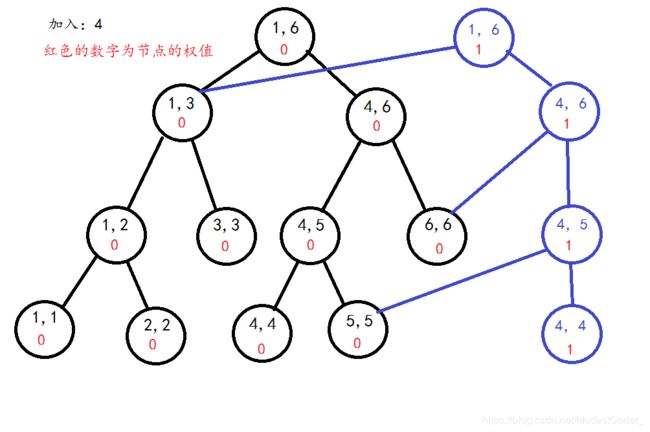
区间[1,2]的线段树（橙色节点为新节点）

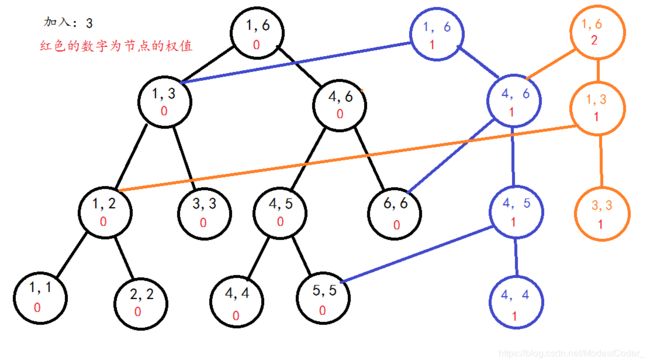
区间[1,3]的线段树（紫色节点为新节点）

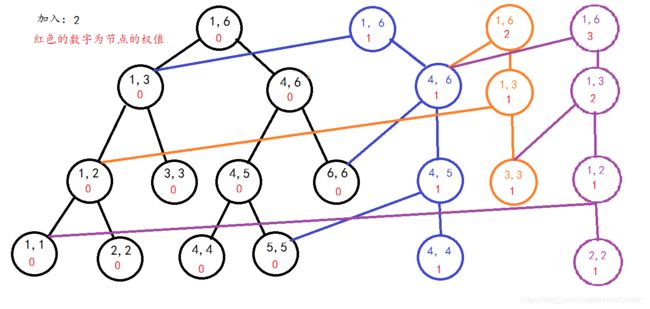
这样是不是非常优秀啊？
主席树的思想就讲到这里，接下来具体的代码来实现它

4、变量

• a、b数组，一般储存输入数据
• sz：节点个数
• rt数组：存储每棵线段树的根节点编号
• lc、rc数组：记录左儿子、右儿子编号，类似于动态开点
• sum数组：记录节点权值
• p：记录离散化后序列长度，也是线段树的区间最大长度

5、主席树

主席树又名可持久化线段树，顾名思义，它可以把问题的历史信息全部记录下来，实现可持久化

首先，数可能会很大，然而n却只有200000，所以要离散化，用到unique函数

	for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];//复制a数组
	sort(b + 1, b + 1 + n);
	q = unique(b + 1, b + 1 + n) - b - 1;//unique函数，返回值为去重后的序列长度

建一棵空树，虽说不建也没关系，不过我初学时题解里都是先建一棵空树，以防万一？反正建一下也不会错

	build(rt[0], 1, q);//空树看成第0棵树

1~n依次建树

	for (int i = 1; i <= n; ++i){
		p = lower_bound(b + 1, b + 1 + q, a[i]) - b;//找出新加入的点的位置，用lower_bound
		rt[i] = update(rt[i - 1], 1, q);
	} 

查询操作

	while (m--){
		int l = read(), r = read(), k = read();
		printf("%d\n", b[query(rt[l - 1], rt[r], 1, q, k)]);//前缀和思想，[1,r]-[1,l-1]=[l,r]
	}

build函数

void build(int &rt, int l, int r){
	rt = ++sz, sum[rt] = 0;//新点
	if (l == r) return;//叶子结点，退出
	int mid = (l + r) >> 1;//mid
	build(lc[rt], l, mid); build(rc[rt], mid + 1, r);//往下走
}

update函数

int update(int o, int l, int r){
	int oo = ++sz;//新点
	lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;//继承原点的信息，权值+1
	if (l == r) return oo;//叶子结点，退出
	int mid = (l + r) >> 1;//mid
	if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);//新加入的节点在哪个区间，就走到哪个区间里去
	return oo;//返回值为新点编号
}

query函数

int query(int u, int v, int l, int r, int k){//u、v为两棵线段树当前节点编号，相减就是询问区间
	int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];//sum相减，前缀和思想
	if (l == r) return l;//叶子结点，找到kth目标，退出
	if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
	//kth操作，排名<=左儿子的数的个数，说明在左儿子，进入左儿子；反之，目标在右儿子，排名需要减去左儿子的权值
}

注意，主席树一般开32倍空间

6、例题

模板题的实现就是上面的内容啦
完整的代码：

#include 
#define maxn 200010
using namespace std;
int a[maxn], b[maxn], n, m, q, p, sz;
int lc[maxn << 5], rc[maxn << 5], sum[maxn << 5], rt[maxn << 5];
//空间要注意

inline int read(){
	int s = 0, w = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;
	for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);
	return s * w;
}

void build(int &rt, int l, int r){
	rt = ++sz, sum[rt] = 0;
	if (l == r) return;
	int mid = (l + r) >> 1;
	build(lc[rt], l, mid); build(rc[rt], mid + 1, r);
}

int update(int o, int l, int r){
	int oo = ++sz;
	lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;
	if (l == r) return oo;
	int mid = (l + r) >> 1;
	if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);
	return oo;
}

int query(int u, int v, int l, int r, int k){
	int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];
	if (l == r) return l;
	if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
}

int main(){
	n = read(), m = read();
	for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];
	sort(b + 1, b + 1 + n);
	q = unique(b + 1, b + 1 + n) - b - 1;
	build(rt[0], 1, q);
	for (int i = 1; i <= n; ++i){
		p = lower_bound(b + 1, b + 1 + q, a[i]) - b;
		rt[i] = update(rt[i - 1], 1, q);
	} 
	while (m--){
		int l = read(), r = read(), k = read();
		printf("%d\n", b[query(rt[l - 1], rt[r], 1, q, k)]);
	}
	return 0;
}

7、复杂度分析

时间复杂度

建树$O(nlogn)$
询问$O(mlogn)$
总复杂度$O((n+m)logn)$

空间复杂度

一般为$O(nlo{g}^{2}n)$

8、练习题

初学者题，用主席树查询区间小于某个数
在树上做主席树，用到树上差分
另一道模板题
差分思想+主席树，难题
dfs序+主席树
以及我个人关于一类题用主席树的想法
可持久化数组模板，用主席树

9、后记

主席树告一段落啦，初学者还是建议多看看代码
首先熟练模板
然后，我个人认为主席树还是很灵活的
建议多练几道题目

据说主席树是一个叫黄嘉泰的人发明的，所写是hjt，所以叫主席树。。

感谢LuoGu刷题平台