Tensorflow学习之逻辑回归的实现
代码:
# coding:utf-8
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
data=[]
label=[]
np.random.seed(0)
##随机产生训练集
for i in range(150):
x1=np.random.uniform(-1,1)
x2=np.random.uniform(0,2)
if x1**2+ x2**2<=1:
data.append([np.random.normal(x1,0.1),np.random.normal(x2,0.1)])
label.append(0)
else:
data.append([np.random.normal(x1,0.1),np.random.normal(x2,0.1)])
label.append(1)
# -1就是让系统根据元素数和已知行或列推算出剩下的列或者行,-1就是模糊控制,(-1,2)
# 就是固定两列,行不知道
data=np.hstack(data).reshape(-1,2)
label=np.hstack(label).reshape(-1,1)
plt.scatter(data[ : ,0], data[ :, 1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()
#知识点:
#tf.add_to_collection:把变量放入一个集合,把很多变量变成一个列表
#tf.get_collection:从一个结合中取出全部变量,是一个列表
#tf.add_n:把一个列表的东西都依次加起来
def get_weight(shape,lambda1):
var=tf.Variable(tf.random_normal(shape),dtype=tf.float32)
tf.add_to_collection('losses',tf.contrib.layers.l2_regularizer(lambda1)(var))
return var
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
sample_size=len(data)
#定义的神经结构每一层的节点个数
layer_dimension=[2,10,5,3,1]
n_layers=len(layer_dimension)
cur_layer=x
#输入层
in_dimension=layer_dimension[0]
#向前遍历
for i in range(1,n_layers):
out_dimension=layer_dimension[i]
weight=get_weight([in_dimension,out_dimension],0.03)
bias=tf.Variable(tf.constant(0.1,shape=[out_dimension]))
##tf.nn.elu是激活函数
cur_layer=tf.nn.elu(tf.matmul(cur_layer,weight)+bias)
in_dimension=layer_dimension[i]
y=cur_layer
mse_loss=tf.reduce_sum(tf.pow(y_-y,2))/sample_size
tf.add_to_collection('losses',mse_loss)
loss=tf.add_n(tf.get_collection('losses'))
train_op=tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS=40000
with tf.Session() as sess:
tf.initialize_all_variables().run()
for i in range(TRAINING_STEPS):
sess.run(train_op,feed_dict={x:data,y_:label})
if(i%2000)==0:
print("After %d steps, mse_loss:%f" % (i,sess.run(mse_loss,feed_dict={x:data,y_:label})))
#画出训练后的分割函数
#mgrid函数产生两个240×241的数组:-1.2到1.2每隔0.01取一个数共240个
xx,yy= np.mgrid[-1.2:1.2:.01,-0.2:2.2:.01]
##np.c_应该是合并两个数组
grid=np.c_[xx.ravel(),yy.ravel()]
probs=sess.run(y,feed_dict={x:grid})
probs=probs.reshape(xx.shape)
plt.scatter(data[:,0],data[:,1],c=label,cmap="RdBu",vmin=-.2,vmax=1.2,edgecolors="white")
plt.contour(xx,yy,probs,levels=[.5],cmap="Greys",vmin=0,vmax=.1)
plt.show()
"""
#带正则化参数训练
train_op=tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS=40000
with tf.Session() as sess:
tf.initialize_all_variables().run()
for i in range(TRAINING_STEPS):
sess.run(train_op,feed_dict={x:data,y_:label})
if i%2000==0:
print("After %d steps, mse_loss:%f"(i, sess.run(loss, feed_dict={x: data, y_: label})))
xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x: grid})
probs = probs.reshape(xx.shape)
plt.scatter(data[:,0],data[:,1],c=label,cmap="RdBu",vmin=-.2,vmax=1.2,edgecolors="white")
plt.contour(xx,yy,probs,levels=[.5],cmap="Greys",vmin=0,vmax=.1)
plt.show()
"""结果:可视化数据:
这时我们可以看到出现里过拟合现象,这时候我们就需要用正则化来防止过拟合。。
正则化后结果:
代码所涉及到的知识点补充:
tensorflow中的激活函数:
tf.nn.relu()
tf.nn.relu6()
tf.nn.sigmoid()
tf.nn.tanh()
tf.nn.elu()
tf.nn.bias_add()
tf.nn.crelu()
tf.nn.relu6()
tf.nn.softplus()
tf.nn.softsign()
tf.nn.dropout()注意:所有激活函数 输入 和 输出 的维度是一样的
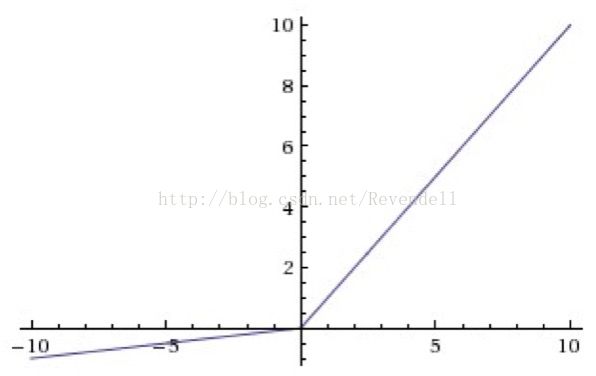
relu()函数:
leaky relu函数:
reLU 中当 x<0 时,函数值为 0。而 Leaky ReLU 则是给出一个很小的负数梯度值,比如 0.01。
sigmod函数:
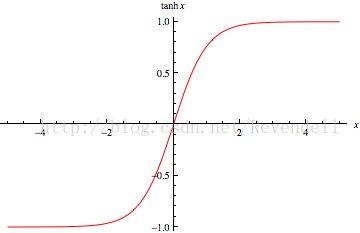
tanh函数:
tensorflow中的正则化方法:
tensorflow中对参数使用正则项分为两步:
1. 创建一个正则方法(函数/对象)
2. 将这个正则方法(函数/对象),应用到参数上
创建正则化方法:
tf.contrib.layers.l1_regularizer(scale, scope=None)
返回一个用来执行L1正则化的函数,函数的签名是func(weights).
参数:
- scale: 正则项的系数.
- scope: 可选的
scope name
tf.contrib.layers.l2_regularizer(scale, scope=None)
返回一个执行L2正则化的函数.
tf.contrib.layers.sum_regularizer(regularizer_list, scope=None)
返回一个可以执行多种(个)正则化的函数.意思是,创建一个正则化方法,这个方法是多个正则化方法的混合体.
参数:
regularizer_list: regulizer的列表
可以看到上面把正则化分成里L1正则化和L2正则化:那两者有何区别呢?
使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)
下图是Python中Lasso回归的损失函数,式中加号后面一项α||w||1即为L1正则化项:
下图是Python中Ridge回归的损失函数,式中加号后面一项α||w||22即为L2正则化项:
可以看到区别如下:
- L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为||w||1
- L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为||w||2
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
将正则化方法应用到参数上:
tf.contrib.layers.apply_regularization(regularizer, weights_list=None)
返回一个标量Tensor,同时,这个标量Tensor也会保存到GraphKeys.REGULARIZATION_LOSSES中.这个Tensor保存了计算正则项损失的方法.
参数:
- regularizer:就是我们上一步创建的正则化方法
- weights_list: 想要执行正则化方法的参数列表,如果为
None的话,就取GraphKeys.WEIGHTS中的weights.
tensorflow中的Tensor是保存了计算这个值的路径(方法),当我们run的时候,tensorflow后端就通过路径计算出Tensor对应的值注意:如果是自己手动定义weight的话,需要手动将weight保存到GraphKeys.WEIGHTS中,但是如果使用layer的话,就不用这么麻烦了,别人已经帮你考虑好了.(最好自己验证一下tf.GraphKeys.WEIGHTS中是否包含了所有的weights,防止被坑)。。还有在使用tf.get_variable()和tf.variable_scope()的时候,你会发现,它们俩中有regularizer形参.如果传入这个参数的话,那么variable_scope内的weights的正则化损失,或者weights的正则化损失就会被添加到GraphKeys.REGULARIZATION_LOSSES中。。。。。。。