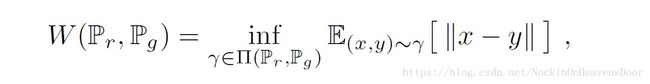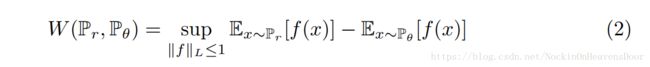wasserstein 距离

注明：直观理解而已，正儿八经的严谨证明看最下面的参考。

Earth Mover’s Distance

推土机距离的例子：有一堆土的分布是 $P_r$, 其随机变量是$x$,现在要求把这堆土挪动成为分布 $P_g$ ，其随机变量是$y$(图上是$P_{\theta }$)，这样做的方法很多，那么做最小功的挪动该是什么？这是一个优化问题对应着的最优解是：

这里 $\Pi (P_r,P_g)$ 表示的是边缘分布是$P_r$ 和 $P_g$ 的联合分布 $(P_r,P_g)$ 集合，即 ${\sum }_x\gamma (x,y)=P_r(y)$ ，${\sum }_y\gamma (x,y)=P_{\theta }(x)$.

$\gamma \in \Pi (P_r,P_{\theta })$, 求解$(x,y)$服从联合分布$\gamma$ 时，关于$||x-y||$的期望，所有的解中最小的期望便是推土机距离。

直观的测度论

测度论提供了一些集合的特征，用来描述适用于${\mathbb{R}}^n$空间的大多数点。
零测度：零测度集合在我们的度量空间中不占有任何的体积。比如二维空间中的一条直线的测度是0。

高维空间的低维子空间

高维空间中的很多点是多余的，真实数据蜷缩在低维子空间的流形上（即高维曲面），因为维度低，所占空间体积几乎为0，所以原始的GANs存在的问题是生成器的生成数据广泛分布在高维空间中，侦测不到真实数据，KL距离始终是log2，所以对生成器的梯度始终是0，怎么训练也没用。

Wasserstein距离的对偶式

相当于找到一个函数 $f$ 求（3）的最大目标函数。这个函数满足$\Vert f{\Vert }_{L\le 1}$, 1-Lipschitz 函数。

补充：2019年4月16日08:11:36

：我在简书里补充了一些资料和定义，需要的可以去看看：https://www.jianshu.com/p/b03d5433229e

---

参考：https://www.zhihu.com/question/41752299
：https://vincentherrmann.github.io/blog/wasserstein/
：《深度学习》《hulu百面》