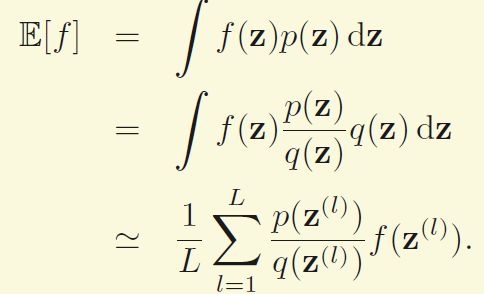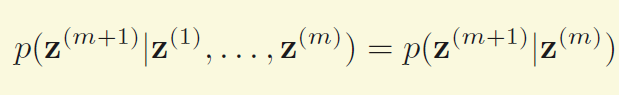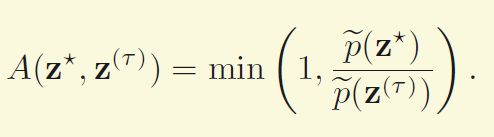PRML抽样方法笔记
0导语
参考 pattern recognition and machine learning 第十一章。主要是笔记,本人没有暂深入和形象的理解。
这里要解决的最基本的问题是要求一个函数f(z)的期望,而z又服从某种分布。
如上图,如果变量是连续的,我们希望要求的是
如果是离散的,就把积分符号换成和。
最基本的想法就是要从P(z)中抽出一些样本Z(l),然后用这些样本的均值来估计上面的期望
1基础采样方法(Basic Sampling)
1.1标准分布
在一般的程序语言中,一般都会提供一些基础的随机数生成器,像均匀分布或者高斯分布。这里先介绍利用均匀分布来产生其他的一些简单的非均匀分布。
假设Z是在区间(0,1)的均匀分布,然后我们希望变量y服从另外一个简单不均匀分布,我们所需要做的就是要找到y = f(z) 这个f函数以使得y的分布符合我们的要求。
因为y=f(z),那么根据基本的概率公式y的分布是
在这里,由于z服从均匀分布,因此p(z)为1,对公式左右两边求定积分
这样就得到了z和y的关系,最后只要求个反函数就可以了。
1.2拒绝采样(Rejection sampling)
上面的方法依赖于求积分和求反函数,有很大的限制,这里要介绍的拒绝采样相对地能适用于复杂些的分布,以单变量为例,如果我们需要从分布p(z)中采样,而p(z)分布不是很简单的标准分布,标准的程序库和上面的方法都处理不了,如下图中红线所画的分布。不过看了下图,相信已经大概猜到了拒绝采样的思想.
就是找一个比较接近然后容易采样的分布q(z)(称之为proposal distribution),并重新反归一化成kq(z),k是一个常数,让在所有的地方kq(z)都大于等于p(z).然后我们首先均匀分布抽出z0,然后在(0,kq(z0))中均匀抽出一个样本u0,如果样本处于上图的灰色部分,即u0>p(z0)则抛弃这个样本,否则采用。这个方法的缺点是高维空间下拒绝率有可能很高,比如3维球体,体积都集中在外层。
1.3 自适应拒绝采样(Adaptive rejectionsampling)
(这部分本人没有很理解--!)拒绝采样中,有时候从现在好采样的分布中比较难找到合适的q(z),这时候我们可以自己构造。它分析的是ln(pz),不过还没理解这么从这些分段的q(z)中采样
1.4 重要性采样(Importance sampling)
重要性采样关注的不再是抽取样本,而是关注求期望这个最原始的目标
假设p(z)是很难抽样的,但是如果我们已知任意z时p(z)的值,那么一种简单的策略是利用积分的思想,把分布进行分割,从而我们直接对z进行均匀分布的抽样,得到
这种方法的一个很明显的缺点就是如果z的维度很大,那么我们所需要抽的样本也需要很多。另外,概率高的地方只占整个空间很小的一块地方是比较常见的,例如高斯分布,所以均匀分布的效率比较低,我们更需要的是概率高的地方的那些样本,更确切的说是需要p(z')f(z')值较大的这些样本,因为这些样本很大程度上决定了期望。
和拒绝采样一样,重要性采样也基于比较好抽样的proposal distribution q(z),然后可以把原始公式写成
第二步到第三步的推导可以看成是期望公式,f(z)p(z)/q(z)当成一个整体的函数,q(z)是分布函数,然么第二个公式就是求f(z)p(z)/q(z)的期望,也就约等于第三个公式。
很显然,重要性采样的难点也是选择q(z)。好处就是一般情况下p(z)f(z)变化很大,很有可能由一块小区域主导了期望的值,因此采样的量可以比较小。但是如果采样的样本没有采到这块主区域,我们也没有什么好的方法可以去看出来。
1.5 重要性重采样(Sampling importanceresampling)
在拒绝采样中,k的选择比较困难,一方面要保证kq(z)大于等于p(z),另外一方面还要需要较小的拒绝率,一般很难选择。
在重要性重采样中,跟之前一样,我们也需要q(z),主要分为这么几步:
1)首先从q(z)中采L个样本z(1),…,z(L)
2)计算这些样本的权重(w1,…,wL)
3)然后从z(1),…,z(L)中以第二步的权重为概率,采取L个样本
当L趋于无穷时,最后取出来的z服从p(z)分布
2 马尔科夫链蒙特卡洛(Markov ChainMonte Carlo)
马尔科夫是俄罗斯数学家的名字,蒙特卡洛应该跟赌博有关系,映像中是受赌博激发才想出来的。
2.1马尔科夫链
为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率
齐次性,如果转移概率恒定不变,则称马尔科夫链具有齐次性
2.2 Metropolis-Hastings采样
第一节介绍的采样算法中,采出来的样本都是独立的,接下来的算法中,样本的抽取是有依赖的。
首先要存下当前时刻的样本zt,然后我们有一个依赖于当前状态的proposal distribution q(z|zt),比如q可以是一个以当前状态为均值,一定方差的高斯分布。在每一步中,我们根据当前样本和分布q产生一个样本候选z*,然后我们采用拒绝采样的思想,以一定的准则拒绝或接受这个样本.
原始的Metropolis采样中,假定对于所有的zA和zB,q(zA|zB) = q(zB|zA),
如果拒绝,上一步的样本作为当前的样本。
下图演示的就是对高斯函数进行采样
在Metropolis-Hastings算法中,条件变成了
具体好处本人还不是很理解--!
2.3 Gibbs 采样 (Gibbs Sampling)
RBM中用了Gibbs采样,Gibbs可以看成是Metropolis-Hastings采样的特殊情况。考虑一个多维变量的分布p(z)= p(z1, . . . , zM),我们想从这个分布中采样,并且假设我们已经有了马尔科夫链的初始状态,那么Gibbs采样的每一步是只改变当前状态的一个变量zi,zi是从条件分布p(zi|z\i)中抽取的,z\i是除了zi外其他所有的变量。xi的选择可以是循环或者是从某个分布中提取。
举个例子,我们有个分布p(z1,z2, z3),并且我们已经有了当前时刻t的状态z1t,z2t,z3t
1)首先我们从下面的分布中抽出一个z1t+1来代替z1t
p(z1|z2t,z3t)
2)接着我们从新的z1t+1和z3t抽出新的z2t+1来代替z2t
p(z2|z1t+1,z3t)
3)同理得到z3t+1
p(z3|z1t+1,z2t+1)
循环1)2)3)。
参考文献
[1]Bishop C M. Pattern recognition[J]. MachineLearning, 2006, 128.
[2] http://blog.csdn.net/xianlingmao/article/details/7768833
[3] https://www.youtube.com/watch?v=h1NOS_wxgGg