Matlab2016做曲线拟合(Curve Fitting)(2)
Polynomial Models(多项式模型)
常见多项式的基本模型:

其中 n + 1 是多项式的阶, n 是多项式的维度, 1 ≤ n ≤9。该顺序给出了合适的系数个数, 并给出了预测变量最高的维度。
在本文中, 多项式按其度来描述。例如, 三维 (立方) 多项式表示如下:
![]()
当需要一个简单的经验模型时, 通常使用多项式。我们可以使用多项式模型进行插值或外推, 或者使用全局拟合来描述数据。例如, 0 至760o 温度范围内的 J 型热电偶的温度-电压转换是用第七维度多项式描述的。
注:如果不需要全局参数拟合, 并且希望最大限度地提高拟合的灵活性, 则分段多项式可能提供最佳方法。有关详细信息, 请参阅非参数拟合。多项式拟合的主要优点包括对数据的合理灵活性不是太复杂,而且它们是线性的,这意味着拟合过程很简单。 主要缺点是高度配合会变得不稳定。 此外,任何程度的多项式都可以在数据范围内提供良好的拟合,但可以在该范围之外疯狂地发散。 因此,在使用多项式进行外推时要格外小心。
当需要拟合高阶多项式时,拟合过程使用预测值作为具有非常大值的矩阵的基础,这可能导致缩放问题。 为了解决这个问题,应该将数据归一化为零均值,并将其标定为单位标准偏差。 通过选择曲线拟合应用中的中心和缩放复选框来标准化数据。
交互式拟合多项式模型
通过输入 cftool 打开曲线拟合应用程序。或者, 单击 “应用程序” 选项卡上的 Curve Fitting。
在曲线拟合应用程序中, 选择曲线或曲面数据。
如果选择曲线数据 (X 数据和 y 数据, 或只针对索引的 y 数据), 曲线拟合应用程序将创建默认的曲线拟合多项式。
如果选择曲面数据 (X 数据、Y 数据和 Z 数据), 曲线拟合应用程序将创建缺省曲面拟合, 插值函数。将模型类型从插值函数更改为多项式。
对于曲线, 多项式模型适合于 x 中的多项式。
对于曲面, 多项式模型适合于 x 和 y 的多项式。

您可以指定以下选项:
x和y输入的维度:
对于曲线,x的度数可以达到9。
对于表面,x和y的度数可以达到5。
多项式的度是x和y度的最大值。 请参阅定义多项式曲面拟合的多项式术语。
使用的鲁棒线性最小二乘拟合方法(Off,LAR或Bisquare)。
通过单击适合选项设置界限或排除术语,可以通过将其边界设置为0来排除任何术语。
在“结果”窗格中查看模型项,系数值和拟合优度统计信息。
如果输入变量具有非常不同的比例,请选中并清除中心并缩放复选框以查看拟合中的差异。 结果窗格中的消息会在缩放时提示提高拟合度。
用拟合函数拟合多项式
此示例演示如何使用 “拟合函数” 将多项式与数据相拟合。步骤拟合和绘制多项式曲线和曲面, 指定拟合选项, 返回拟合统计的优点, 计算预测, 并显示置信区间。
多项式库模型是拟合和 fittype 函数的输入参数。指定模型类型poly后跟 x (最多 9) 的度数, 或 x 和 y (最多 5)。例如, 指定一个具有 “poly2” 或具有 “poly33” 的立方曲面的二次曲线。
这里需要解释poly是什么:
poly:Polynomial with specified roots or characteristic polynomial:具有指定根或特征多项式的多项式
常用语法:
p = poly(r)
p = poly(A)p=poly(r), 其中是r向量, 返回的是多项式的系数, 其根是 r 的元素。
p = poly(A),其中 A 为 n*n的 矩阵, 返回矩阵的特征多项式 (λI-A) 的 n+1 系数。
举例:计算矩阵的特征值, A。
>> A = [1 8 -10; -4 2 4; -5 2 8]
A =
1 8 -10
-4 2 4
-5 2 8
>> e=eig(A)
e =
11.6219 + 0.0000i
-0.3110 + 2.6704i
-0.3110 - 2.6704i
>> p=poly(e)
p =
1.0000 -11.0000 -0.0000 -84.0000由于 e 中的特征值是 A 的特征多项式的根, 所以利用poly来确定 e 中的特征多项式。
创建和绘制二次多项式曲线
加载一些数据并拟合一个二次多项式。用字符串 “poly2” 指定二次或二度多项式
load census;
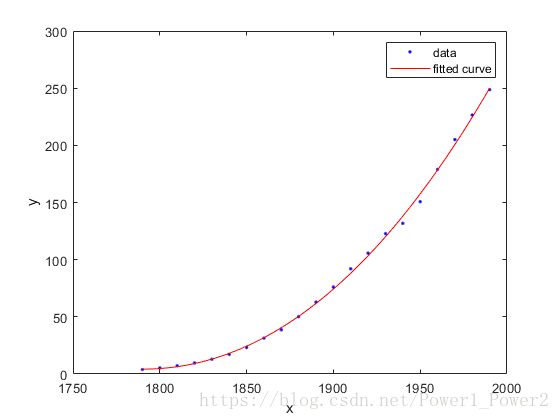
fitpoly2=fit(cdate,pop,'poly2')
% Plot the fit with the plot method.
plot(fitpoly2,cdate,pop)
% Move the legend to the top left corner.
legend('Location','NorthWest' );生成结果如下:
fitpoly2 =
Linear model Poly2:
fitpoly2(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)fitpoly3=fit(cdate,pop,'poly3')
plot(fitpoly3,cdate,pop)结果:
fitpoly3 =
Linear model Poly3:
fitpoly3(x) = p1*x^3 + p2*x^2 + p3*x + p4
Coefficients (with 95% confidence bounds):
p1 = 3.855e-06 (-4.078e-06, 1.179e-05)
p2 = -0.01532 (-0.06031, 0.02967)
p3 = 17.78 (-67.2, 102.8)
p4 = -4852 (-5.834e+04, 4.863e+04)fit3=fit(cdate, pop,'poly3','Normalize','on','Robust','on')
plot(fit3,cdate,pop)输出:
fit3 =
Linear model Poly3:
fit3(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = -0.4619 (-1.895, 0.9707)
p2 = 25.01 (23.79, 26.22)
p3 = 77.03 (74.37, 79.7)
p4 = 62.81 (61.26, 64.37)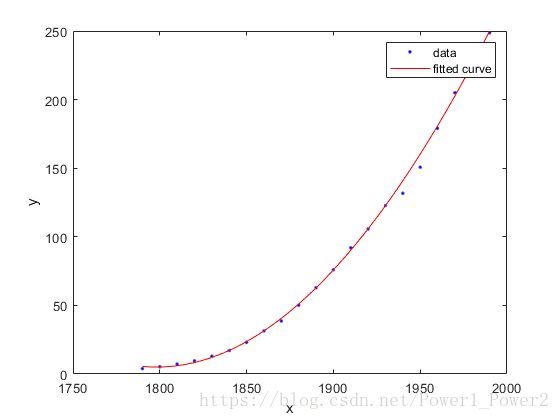
要了解可以为库模型 “poly3” 设置哪些参数, 请使用 fitoptions 函数。
fitoptions poly3ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Robust: 'Off'
Lower: [1x0 double]
Upper: [1x0 double]指定 “gof” 输出参数以获取三次多项式拟合的拟合性统计信息。
[fit4, gof]=fit(cdate, pop,'poly3','Normalize','on');
gof绘制残差以评估拟合
若要绘制残差, 请在绘图方法中指定 “残值” 作为绘图类型。
plot(fit4,cdate, pop,'residuals');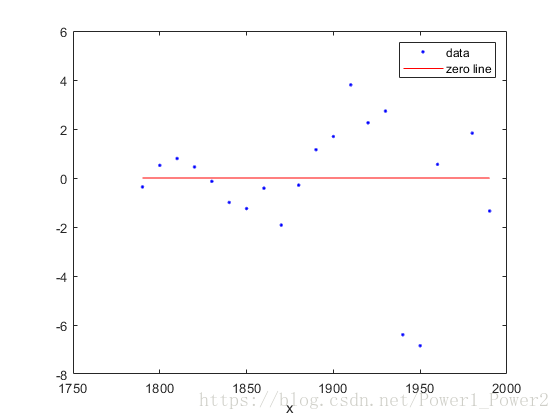
检查超出数据范围的匹配项
默认情况下, 拟合在数据范围内绘制。若要在不同的范围内绘制一个拟合, 请在绘制匹配项之前设置坐标轴的 x 限制。例如, 若要查看从拟合推断出的值, 请将上限 x 限制设置为2050。
plot( cdate, pop, 'o' );
xlim( [1900, 2050] );
hold on
plot( fit4 );
hold off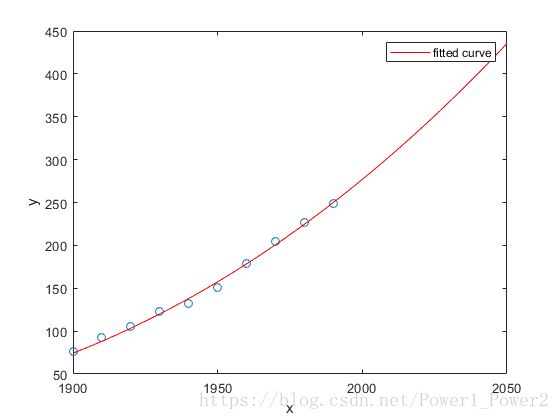
绘制预测边界
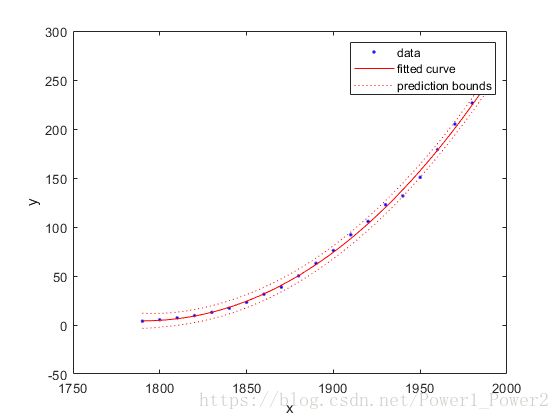
若要绘制预测边界, 请使用 “predobs” 或 “predfun” 作为绘图类型。
plot(fit4,cdate,pop,'predobs')plot( cdate, pop, 'o' );
xlim( [1900, 2050] )
hold on
plot( fit4, 'predobs' );
hold off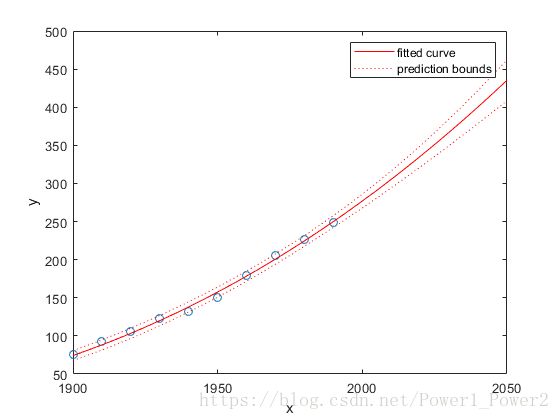
现在我们就可以获取新查询点的信任界限并评估拟合一些新的查询点。
cdateFuture = (2000:10:2020).';
popFuture = fit4( cdateFuture )输出:
popFuture =
276.9632
305.4420
335.5066使用 predint 方法计算未来人口预测95% 的置信限。
ci = predint( fit4, cdateFuture, 0.95, 'observation' )输出:
ci =
267.8589 286.0674
294.3070 316.5770
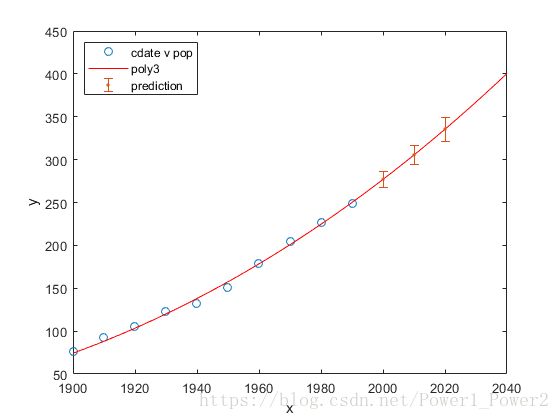
321.5924 349.4208可视化预测:
plot(cdate, pop, 'o');
xlim([1900, 2040])
hold on
plot(fit4)
h = errorbar(cdateFuture,popFuture,popFuture-ci(:,1),ci(:,2)-popFuture,'.');
hold off
legend('cdate v pop','poly3','prediction','Location','NorthWest')拟合和绘制多项式曲面
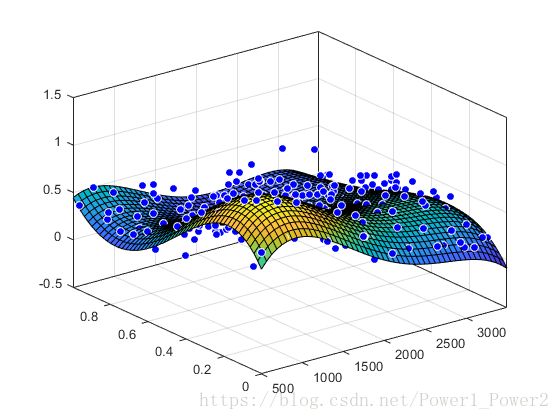
加载一些曲面数据, 并在 x 和 y 中拟合第四度多项式。
load franke;
fitsurface=fit([x,y],z, 'poly44','Normalize','on')
plot(fitsurface, [x,y],z)输出:
Linear model Poly44:
fitsurface(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3
+ p21*x^2*y + p12*x*y^2 + p03*y^3 + p40*x^4 + p31*x^3*y
+ p22*x^2*y^2 + p13*x*y^3 + p04*y^4
where x is normalized by mean 1982 and std 868.6
and where y is normalized by mean 0.4972 and std 0.2897
Coefficients (with 95% confidence bounds):
p00 = 0.3471 (0.3033, 0.3909)
p10 = -0.1502 (-0.1935, -0.107)
p01 = -0.4203 (-0.4637, -0.377)
p20 = 0.2165 (0.1514, 0.2815)
p11 = 0.1717 (0.1175, 0.2259)
p02 = 0.03189 (-0.03351, 0.09729)
p30 = 0.02778 (0.00749, 0.04806)
p21 = 0.01501 (-0.002807, 0.03283)
p12 = -0.03659 (-0.05439, -0.01879)
p03 = 0.1184 (0.09812, 0.1387)
p40 = -0.07661 (-0.09984, -0.05338)
p31 = -0.02487 (-0.04512, -0.004624)
p22 = 0.0007464 (-0.01948, 0.02098)
p13 = -0.02962 (-0.04987, -0.009366)
p04 = -0.02399 (-0.0474, -0.0005797)