LeetCode_04_BinarySearch笔记总结

摘要

今天的题目也是二分查找，其中涉及到开方，找重复数，还有二分超找的一些变形，如找Peak，二分查找树问题

正文

1. LC69. Sqrt(x)

---

题目：
Implement int sqrt(int x).
Compute and return the square root of x.
x is guaranteed to be a non-negative integer.
Example 1:
Input: 4
Output: 2
Example 2:
Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842…, and since we want to return an integer, the decimal part will be truncated.
使用公司:
Facebook, Bloomberg, Apple
难度:
容易

---

题目与思路分析:
这个题的意思就是说求开根号，如果是开不成整数的比如8，那就取整数部分. 思路:这个题我们首先要知道，n开根号肯定小于n/2. 并且我们可以将n想成是1到n的排序数列,这样我们就能够用二分法了. 这样的话，我们就看mid*mid和n比较了. 这里注意的第一点是: 不要共mid的平方，因为这样的话会使得结果溢出，除非用long类型，但是我们可以x/mid=mid这种形式. 在一个涉及到while(left<=right)的烦心事. 大家还是不要记那些模板了，还是想清原理比较好处理. 当我们left<=right的时候，倒数第二步的时候left和right相邻, 但是这时取到的mid肯定是left的值，如果不相等那么就是肯定是小,那么left就会右移动,这时，left=right了，这时候，mid还不相等的话，肯定是大，那么right就会左移了, 这样循环就结束了. 所以我们自然需要right值了.
直接上代码:

class Solution {
    public int mySqrt(int x) {
        if(x == 0){
            return 0;
        }
        int left = 1; 
        int right = x;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(mid == x / mid){
                return mid;
            }
            if(mid > x / mid){
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
       return right;
    }
}

2. LC230. Kth Smallest Element in a BST

---

题目：
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
使用公司:
Google, Bloomberg, Uber
难度:
中等

---

题目与思路分析:
题目说给定了一个二分查找树，然后让我们找出第K个最小的值. 首先我们知道二分查找树就是中序遍历的树. 这样的情况下，我能首先想到的方法肯定是二分. 我们知道左树肯定是小于中间小于右树的, 那么我们就计算节点个数. 用递归的方式，如果K>左树的节点个数，那么就说明K在左树上.但是需要注意的一点是, 因为我们是用的分治思想，所以左树和右树的操作可以看成是独立的. 那么在递归得出右树的节点个数的时候,传入的K是k-left-root的值，因为对于右树来说，你是计算的时候在右面这块第几小的，放在全局就得+左和根.

class Solution {
    public static int res = 0;
    public int kthSmallest(TreeNode root, int k) {       
        helper(root, k);
        return res;
    }
    private int helper(TreeNode root, int k){
        if(root == null){
            return 0;
        }
        int leftNodeCount = helper(root.left, k);
        int rightNodeCount = helper(root.right, k - leftNodeCount - 1);
        if(k == leftNodeCount + 1){
            res = root.val;
        }
        return 1 + leftNodeCount + rightNodeCount;
    }
}

3. LC287. Find the Duplicate Number

题目：
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
使用公司:
Bloomberg
难度:
中等

---

题目与思路分析:
这个题就是说数字是1到n但是有n+1个数, 这就说明肯定有一个是重复的. 那么我们找出这个重复的数字是什么. 这个题还是有些意思的, 很类似与单链表的回环问题. 我们按照这个思路去做, 定义一个快速指针和一个慢速指针，快速指针每次走两格，慢速指针每次走一格，当他们第一次相遇的时候，将快速指针从头开始每次一格的走，慢速指针因为碰见了环路会一直循环在那块儿走着，这样再次相遇的时候就是重复的值.

class Solution {
    public int findDuplicate(int[] nums) {
        if(nums == null || nums.length == 0){
            return -1;
        }
        int slow = nums[0];
        int fast = nums[nums[0]];
        while(slow != fast){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        fast = 0;
        while(slow != fast){
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
}

4. LC350. Intersection of Two Arrays II

题目：
Given two arrays, write a function to compute their intersection.
Example:
Given nums1 = [1, 2, 2, 1], nums2 = [2, 2], return [2, 2].
使用公司:
无
难度:
简单

---

题目与思路分析:
这个题的意思就是说给定两个数组将它们的交集打出来. 这个题的思路有很多，这里我用的一种思路就是: 因为有很多重复项的存在并且重复项可能是不连续的，但是都属于相交相并且都要进行打印, 那么我就用HashMap维护一下，key是nums1的值，value是出现了几次. 这样在进行遍历nums2的时候，我只需要看nums2的值在map中存在不，如果存在就减一次1，然后加入到好操作的list中，当value值=0的时候说明nums1中已经没了，nums2中再有也不是交集了.
直接上代码:

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Map map = new HashMap();
        List list = new ArrayList();
        if(nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0){
            return new int[list.size()];
        }
        for(int i = 0; i < nums1.length; i++){
            if(map.containsKey(nums1[i])){
                map.put(nums1[i], map.get(nums1[i]) + 1);
            }else{
                map.put(nums1[i], 1);
            }
        }
        for(int i = 0; i < nums2.length; i++){
            if(map.containsKey(nums2[i]) && map.get(nums2[i]) > 0){
                list.add(nums2[i]);
                map.put(nums2[i], map.get(nums2[i]) - 1);
            }
        }
        int[] res = new int[list.size()];
        for(int i = 0; i < list.size(); i++){
            res[i] = list.get(i);
        }
        return res;
    }
}

5. LC162. Find Peak Element

题目：
A peak element is an element that is greater than its neighbors.
Given an input array where num[i] ≠ num[i+1], find a peak element and return its index.
The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.
You may imagine that num[-1] = num[n] = -∞.
For example, in array [1, 2, 3, 1], 3 is a peak element and your function should return the index number 2.
使用公司:
Google, Microsoft
难度:
中等

---

题目与思路分析:
这个题的意思就是说在给定的数组中，它的样子类似这样:

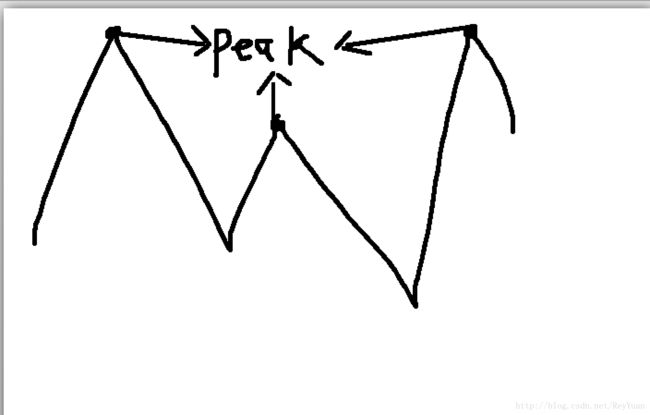
让我们找的就是这写峰值，随便一个返回就行如果有多个峰值的话. 这种题肯定是用二分，但是又不是有序的数列，如何用二分，那我们就获取中值然后看中值和邻居的大小关系，如果nums[mid]>nums[mid+1]&&nums[mid]

class Solution {
    public int findPeakElement(int[] nums) {
        if(nums == null || nums.length == 0){
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        while(left < right - 1){
            int mid = left + (right - left) / 2;
            if(nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]){
                return mid;
            }
            if(nums[mid] > nums[mid + 1] && nums[mid] < nums[mid - 1]){
                //下坡
                right = mid - 1;
            }else if(nums[mid] < nums[mid + 1] && nums[mid] > nums[mid - 1]){
                left = mid + 1;
            }else{
                //谷底
                left = mid;
            }
        }
        if(nums[left] > nums[right]){
            return left;
        }else{
            return right;
        }
    }
}

5. LC367. Valid Perfect Square

题目：
Given a positive integer num, write a function which returns True if num is a perfect square else False.
Note: Do not use any built-in library function such as sqrt.
Example 1:
Input: 16
Returns: True
Example 2:
Input: 14
Returns: False
使用公司:
Linkdln
难度:
简单

---

题目与思路分析:
这题其实就是说能不能开根号后是整数，这个题是上面sqrt的变形，所以很简单，一样的思路，但是有一点是如果mid=num/mid,这种情况下，我们不能马上返回，因为在mid和num/mid比较的时候我们有可能是失精度的，所以一定要判断这个mid是不是能被num整除, 如果能整除并且平方为num说明就是true，因为a*a=b,首先一定是a能被整除. 但如果我们用long来处理就没这个问题存在了.

class Solution {
public boolean isPerfectSquare(int num){ 
        if(num <= 0) return false;
        int left = 1, right = num;
        while(left <= right){
            int mid = left + (right - left)/2;
            //用除法可以避免溢出
            if(mid > num / mid){
                right = mid - 1;
            }else if(mid < num / mid){
                left = mid + 1;
            }else{
                return num % mid == 0;
            }
        }
        return false;
    }
}

Long处理

class Solution {
    public boolean isPerfectSquare(int num) {
        long left = 0;
        long right = num;
        if(num == 0 || num == 1){
            return true;
        }
        while(left <= right){
            long mid = left + (right - left) / 2;

            if(mid*mid == (long)num){
                return true;
            }
            if(mid*mid > (long)num){
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return false;
    }
}

总结

今天的题目也是二分查找，其中涉及到开方，找重复数，还有二分超找的一些变形，如找Peak，二分查找树问题
首先我们对前面讨论的left