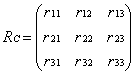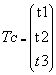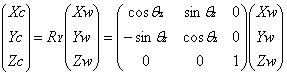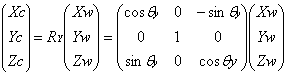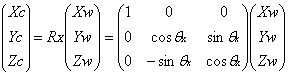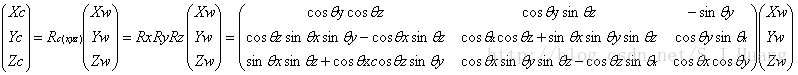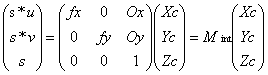世界坐标系与摄像机坐标系的变换

该文章是对《计算机视觉增强现实应用概论》中《增强现实的摄像机空间理论》这一节进行摘录和公式推导。

      摄像机得到的是一个二位平面图像，而增强现实的元素是三维动画。增强现实系统可以将摄像机获取的外部世界图像通过矩阵变化，重构出一个三维的虚拟空间。该空间以摄像机为坐标原点，称为摄像机坐标系。而以实物为原点建立的坐标系称为世界坐标系。

       摄像机运用棱镜将获取到的图像通过小孔成像的方式缩小倒立着呈现在摄像机内部的感光组件上。

                            

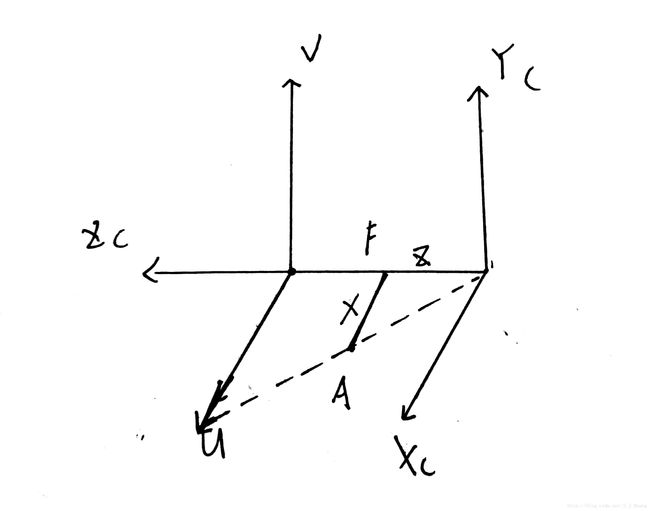
                                                                   摄像机棱镜三维原理投影图

      焦距F是棱镜与摄像机感光片上投影出的图像的距离，从图中来看的话，感光片是在棱镜的前面，这可能与摄像机的构造或成正像有关。Oc为摄像机坐标系的原点，对应的三个轴分别为Xc、Yc、Zc，其中Zc称为主坐标轴。C为图像的坐标原点，位于图像中心，U、V分别为它的横纵坐标。

      由图可知，U和Xc、V和Yc分别相互平行

                                     

假设A点的坐标为（x，0），则根据三角形相似理论，投影到图像上的坐标为U=F*X/Z;同理，V=F*Y/Z。

在这有个问题不太清楚，摄像机坐标的（x,y）一定在感光片的范围内吗？有待解决。

由以上分析还可得出，将真实环境中的三维物体呈现在摄像机的平面图像上，需要经过两个步骤：

（1）将世界坐标系上的一个点通过在三个轴上的旋转以及位移变换，得到其在摄像机坐标系中的位置。

（2）将该点的摄像机坐标系位置通过摄像机自身的投影矩阵投影到平面图像上。

第一步：

      由上面的摄像机棱镜三维原理投影图可知，将摄像机坐标系进行旋转后再平移，可与世界坐标系完全重合。

也就是说，这两个坐标系可以通过旋转和平移来实现相互转换，这可通过一个变换矩阵实现，这个矩阵称为摄像机的外部参数矩阵。

      这个矩阵是怎么得到的呢？现在作如下定义：

      为世界坐标系中的坐标；

      为摄像机坐标系对应的坐标；

       Rcam是摄像机在世界坐标系中的旋转角度,即摄像机经过这个旋转矩阵变换可与世界坐标系平行；

       Tcam是摄像机在世界坐标系中的位移量，即摄像机经过Rcam后再经过Tcam平移可得到世界坐标系；

       Rc是作用于Pw并将其转换到摄像机坐标的旋转矩阵，（具体推导代数学的不好，没推，但很好理解，这两个旋转过程是互为逆过程的嘛）

       Tc是作用于Pw的位移矩阵，Tc=Tcam。

其中，，。

根据前面的分析，将摄像机旋转平移可得到世界坐标系，即

                                                                 

将上式进行变换，可得

                                                        

由于Tc=Tcam,，所以

                                                             

于是乎，只要知道旋转矩阵Rc和平移矩阵Tc的具体参数，便可求出摄像机坐标，完成first step。

怎么求呢？且往下看。

（1）首先假定位移变换为0，只有旋转变换，即。为了便于理解，首先假设世界坐标系的旋转变化只围绕Z轴旋转，不旋转X轴和Y轴。

          

上图中，黑色代表世界坐标系，蓝色代表经旋转后得到的摄像机坐标系，设旋转角度为，根据上图的几何关系可以得到：

                                                         

                                                          

                                                                                   

所以Pc=RcPw可以展开为如下形式：

                                                  

同理可以得出只旋转Y轴和只旋转X轴情况下的旋转矩阵。

                                                   

                                                   

由于整个旋转过程可拆分为分别只绕某一轴旋转，所以Rc可得

敲得好心累啊，谁叫他是复杂的旋转呢。。

外部参数矩阵是由旋转矩阵和平移矩阵构成，Rc求出了，下一个要解决的就是Tc，这个比较直观，将Pw减去两个坐标系原点差值即可。

根据，得

                                  

上式只是为了说明，不一定满足矩阵相乘的条件，计算时可再添加行或列。

第二步：

第二步是通过内部参数矩阵来实现的。

内部参数矩阵的作用是将摄像机坐标系下的三维物体投影到感光片的二维平面上。

二位平面图像一般是以像素为单位计算长和宽的。内部参数包括：焦距F（米），单个像素宽Sx（米）和高Sy（米），焦距f=F/s(像素),图像中心点（Ox,Oy）（像素），棱镜的畸变参数k(一般可以忽略）.

                                

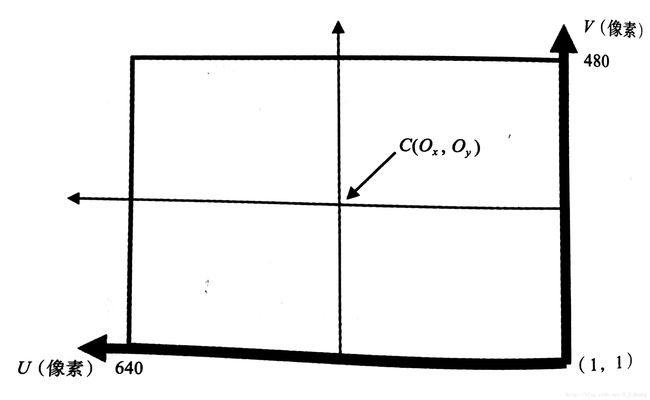
                                                                                      图像平面示意图

 上图中有两个坐标系，一个是以图像中心为原点的图像坐标系，单位为米；另一个是以像素为单位的像素坐标系。前面提到计算图像坐标是以图像坐标系来计算的，转换为像素坐标系则为

                                                       u=(F/Sx)*(Xc/Zc)+Ox=fx*(Xc/Zc)+Ox

                                                       v=(F/Sy)*(Yc/Zc)+Oy=fy*(Yc/Zc)+Oy

所以，同一个平面点的像素单位表示（u,v）和常规单位表示（米）(x,y)之间的关系为：

                                                          u=x/Sx+Ox

                                                          v=y/Sy+Oy

令S=（0，0，1），转换为矩阵表达形式为：

                                        

Mint即为内部矩阵。

一般来说，摄像机的内部参数矩阵是未知的，需要人工测量得到，这一过程称为摄像机校准。

整个变换过程完成了，第一次写这么长的博客，有点tired。简单总结如下：

end at Library Wenzheng Li