Sklearn__支持向量机

支持向量机的基本思想是找到一条"线"，使得分类间距最大。

一、线性分类器(线性核)

很多时候由于数据不可能完全分为两类，所以需要设置一定范围，允许分类错误。即设置软间隔，在sklearn 中用超参数 C （惩罚系数)来控制这种平衡：C 比较小，即脾气较小，度量大容忍度高，其对于的软间隔就大；反之则小。

1. Iris数据集试验一个线性核SVM

一下为十分简单的试验

# 加载包
from sklearn import datasets
from sklearn.pipline import Pipeline
from sklearn.preprocessing import StandarScaler
from sklearn.svm import LinearSVC

def get_iris():
	# 仅仅需要花瓣长宽
	iris = datasets.load_iris()
	return iris.data[:, (2, 3)], (iris.target == 2) * 1.0  # Iris-Virginica

def clf_correct(y_train, y_prd):
	return sum((y_train - y_prd) == 0) / len(y_train)

if __name__ == '__main__':
	x, y = get_iris()
	svm_clf = Pipeline([
		("scaler", StandardScaler()),  # 实际上在算'距离'，所以需要标准化
		("linearsvc", LinearSVC(C=1, loss='hinge')),
	])
	svm_clf.fit(x, y)
	print(svm_clf.predict([[5.5, 1.7]]))

	# 预测
	y_prd = svm_clf.predict(x)
	print("当前模型的准确率为： {}".format(clf_correct(y, y_prd)))

""" result
[1.]
当前模型的准确率为： 0.9533333333333334
"""

需要注意的是，不同于Logistic回归分类，SVM 分类不会输出每个分类的概率。

当然还可以用SVC类，使用SVC(C = 1, kernel = ‘linear’) ， 但是比较慢，尤其是在比较大训练，所以一般不被推荐，另外选择是使用SGDCLassifier 类，即SGDCLassifier(loss = 'hinge', alpha = 1/(m * c))
它应用了随机梯度下降来训练一个线性SVM分类器。尽管它不会和LinearSVC一样快速收敛，但是对于处理那些不适合放在内存的大数据集非常有用，或者在线分类任务同样有用。

二、非线性核

1. 多项式特征变化

一个简单例子

from sklearn.preprocessing import PolynomialFeatures  # 多项式特征变换
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn.metrics import confusion_matrix

def plot_moom(m_x, m_y):
	x_1 = [ m_x[i][0] for i in range(len(m_x))]
	x_2 = [ m_x[i][1] for i in range(len(m_x))]
	plt.scatter(x_1, x_2, c = m_y)


if __name__ == '__main__' :
	make_moons = datasets.make_moons()
	m_x = make_moons[0]
	m_y = make_moons[1]

	poly_svm_clf = Pipeline([
		('poly_features', PolynomialFeatures(degree=3)),
		('scaler', StandardScaler()),
		('svm_clf', LinearSVC(C=10, loss='hinge'))
	])
	poly_svm_clf.fit(m_x, m_y)
	# 预测
	y_prd = poly_svm_clf.predict(m_x)
	print("当前模型的准确率为： {}".format(clf_correct(m_y, y_prd)))
	## 评测
	print(confusion_matrix(m_y, y_prd))
	plot_moom(m_x, m_y)
	plot_moom(m_x, y_prd)
	plt.show()

""" result
当前模型的准确率为： 1.0
[[50  0]
 [ 0 50]]
"""

数据具有明显的多项式分界线所以分类相对简单，且准确

2. 核方法

from sklearn.svm import SVC

if __name__ == '__main__' :
	poly_kernel_svm_clf = Pipeline([
		('scaler', StandardScaler()),
		('svm_clf', SVC(kernel='poly', degree=3, C=5, coef0=1))  ##coef0控制了高阶多项式与低阶多项式对模型的影响
	])
	poly_kernel_svm_clf.fit(m_x, m_y)
	y_prd = poly_kernel_svm_clf.predict(m_x)
	print("当前模型的准确率为： {}".format(clf_correct(m_y, y_prd)))
	## 评测
	print(confusion_matrix(m_y, y_prd))

""" result
当前模型的准确率为： 1.0
[[50  0]
 [ 0 50]]
"""

3. 高斯核

if __name__ == '__main__' :
	rbf_kernel_svm_clf = Pipeline([
		("scaler", StandardScaler()),
		('svm_clf', SVC(kernel='rbf', gamma=5, C=0.001))
	])
	rbf_kernel_svm_clf.fit(m_x, m_y)
	y_prd = rbf_kernel_svm_clf.predict(m_x)
	print("当前模型的准确率为： {}".format(clf_correct(m_y, y_prd)))
	## 评测
	print(confusion_matrix(m_y, y_prd))

""" result
当前模型的准确率为： 1.0
[[50  0]
 [ 0 50]]
"""

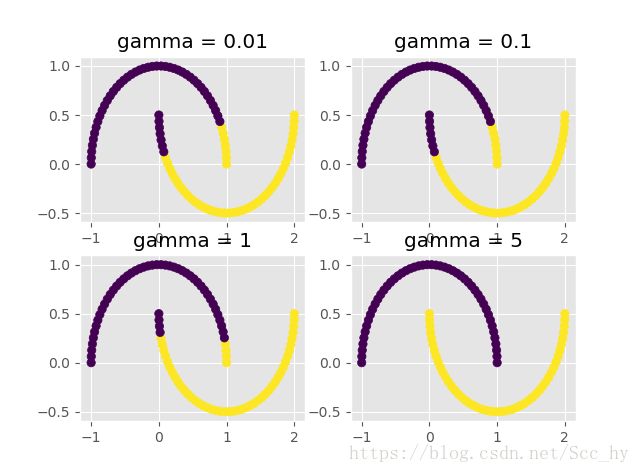
绘图查看gamma 值对分类结果的影响

def plot_gamma(gamma):
	rbf_kernel_svm_clf = Pipeline([
		("scaler", StandardScaler()),
		('svm_clf', SVC(kernel='rbf', gamma=gamma, C=0.001))
	])
	rbf_kernel_svm_clf.fit(m_x, m_y)
	y_prd = rbf_kernel_svm_clf.predict(m_x)
	print("当前模型的准确率为： {}".format(clf_correct(m_y, y_prd)))
	plot_moom(m_x, y_prd)
	plt.title("gamma = {}".format(gamma))

if __name__ == '__main__' :
	plt.subplot(2,2,1)
	a = plot_gamma(0.01)
	plt.subplot(2,2,2)
	b = plot_gamma(0.1)
	plt.subplot(2,2,3)
	c = plot_gamma(1)
	plt.subplot(2,2,4)
	d = plot_gamma(5)
	plt.show()

"""
当前模型的准确率为： 0.86
当前模型的准确率为： 0.86
当前模型的准确率为： 0.92
当前模型的准确率为： 1.0
"""

由上图可以看出 gamma 值影响分类结果：增加gamma 值会使得分类更加精确，即判断边界最终会变的不规则，围绕单个样本周围环绕。 反之，钟型曲线会更加的宽， 样本具有更宽的影响范围，判定边界更加的平滑。
所以gamma 是可调参数: 如果模型过拟合，需要减小 gamma 值； 若欠拟合，则增加 gamma 值

三、核的选择

1、计算复杂度

LinearSVC类基于liblinear库，它实现了线性SVM的优化算法。它并不支持核技巧，但是它样本和特征的数量几乎是线性的：训练时间复杂度大约为O(M*N)
当需要非常高的精度，那么算法就回更加耗时。这是由于 容差值超参数E (在Sklearn 称为 tol)控制的。大多分类任务中，使用默认容差值的效果是已经可以满足一般要求。

SVC类基于libsvm库，它实现了支持核技巧的算法。训练时间复杂度通常介于 $O(m^2\ast n)$ 和 $O(m^3\ast n)$ 之间。这个算法对于复杂但小型或者中等数量的数据集表现是完美的。

2. 核的一般选择

一般来说先用线性核 LinearSVC ，尤其是当训练集十分大的时候或者有大量的特征的情况下。如果训练集不大，可以尝试高斯径向核，它在大多数情况下都很有效。

其他的核函数较少使用，例如，一些核函数是专门用于特定对数据结构的。在对文本文档或者DNA序列进行分类时，有时候会使用字符串核（例如，使用 SSK核(string subsequence kernel) 或者
基于编辑距离的核函数）。

四、SVM回归

SVM算法应用广泛: 不仅仅支持线性核非线性的分类任务,还支持线性和非线性的回归任务。
技巧在于【逆转目标】：限制间隔违规的情况下，不是试图在两个类别之间找到尽可能大的间隔。
SVM回归任务是限制间隔违规情况下，尽可能防止更多的样本在街道上。
"街道"的宽度由超参数E (epsilon)控制，
添加更多的数据样本在间隔之内并不会影响模型的预测，因此，这个模型认为是不敏感的 （ϵ-insensitive）。
在sklearn 中用 LinearSVR 实现SVM回归

1. 线性回归

from sklearn.svm import LinearSVR
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict
def get_line_data():
	np.random.seed(1314)
	x = np.linspace(0, 2, 30)
	y = 1 + 3 * x + 2 * np.random.rand(len(x))
	plt.scatter(x, y)
	plt.show()
	x_in_t = x.reshape((-1, 1))
	return np.c_[np.ones((30, 1)), x_in_t], y.reshape((-1, 1))

def svm_reg_prd(x_in, y_in, epsilon):
	svm_reg = LinearSVR(epsilon = epsilon)  # 缩小街区的大小可以增加回归的准确性
	svm_reg.fit(x_in, y_in)
	return svm_reg.predict(x_in)

def plt_two_prd(x, y_prd, y_prd_l):
	plt.scatter(np.array(x).reshape((-1, 1)), y_in)
	plt.plot(x, y_prd, c='green', lw = 2.5, alpha=0.7)
	plt.plot(x, y_prd_l, c='red', lw = 2.5, alpha=0.7)

if __name__ == '__main__' :
	# SVR
	x_in , y_in =get_line_data()
	x = [x_in[i][1] for i in range(len(x_in))]
	y_prd1 = svm_reg_prd(x_in, y_in, 0.25)
	y_prd2 = svm_reg_prd(x_in, y_in, 0.5)
	y_prd3 = svm_reg_prd(x_in, y_in, 1.0)

	# linearregression
	l_reg = LinearRegression()
	l_reg.fit(x_in, y_in)
	y_prd_l = l_reg.predict(x_in)

	## 图示两个回归,及其他epsilon的表现
	plt.subplot(131)
	plt_two_prd(x, y_prd1, y_prd_l), plt.title("epsilon = 0.25")
	plt.subplot(132)
	plt_two_prd(x, y_prd2, y_prd_l), plt.title("epsilon = 0.5")
	plt.subplot(133)
	plt_two_prd(x, y_prd2, y_prd_l), plt.title("epsilon = 1.0")
	plt.show()
	
	## 评估
	mse_svr1 = np.var(y_prd1.reshape((-1, 1)) - y_in)
	mse_svr2 = np.var(y_prd2.reshape((-1, 1)) - y_in)
	mse_svr3 = np.var(y_prd3.reshape((-1, 1)) - y_in)
	mse_lreg = np.var(y_prd_l.reshape((-1, 1)) - y_in)
	print("SVM回归(epsilon=0.25)MSE为：%.3f;  SVM回归(epsilon=0.5)MSE为：%.3f;\nSVM回归(epsilon=1.0)MSE为：%.3f;  线性回归MSE为：%.3f"%(mse_svr1,mse_svr2,mse_svr3, mse_lreg))

"""
SVM回归(epsilon=0.25)MSE为：0.394;  SVM回归(epsilon=0.5)MSE为：0.385;
SVM回归(epsilon=1.0)MSE为：0.376;  线性回归MSE为：0.374
"""

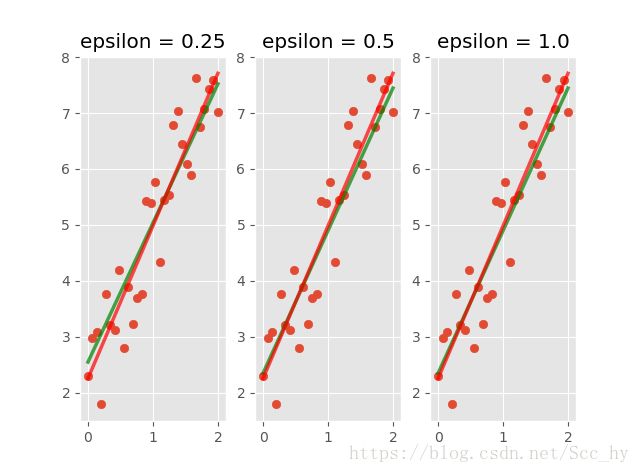
从均方误差和图，我们可以看出当 epsilon 增大的时候回归会更加精确，即 epsilon 控制着街区的大小，当epsilon 街区限制会变高，因而街区会变小。

（在LinearSVR中）本质是 ：不敏感损失函数中的Epsilon参数：添加更多的数据样本在间隔之内并不会影响模型的预测

2. 非线性回归（SVR）

简单实现

from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import  Pipeline
from sklearn.preprocessing import PolynomialFeatures

def get_poly_data():
	np.random.seed(1212)
	x = np.linspace(-2, 2, 60)
	y_2 = 3 * x ** 2 + 2 * np.random.rand(len(x)) + 0.3
	x_in_t1 = x.reshape((-1, 1))
	return np.c_[np.ones((len(x), 1)), x_in_t1], y_2.reshape((-1, 1))

def svm_poly_prd(x_in, y_in, C = 100.0 , epsilon = 0.1):
	svm_ploy_reg = SVR(kernel='poly', degree = 2, C = C, epsilon = epsilon)
	svm_ploy_reg.fit(x_in, y_in)
	return svm_ploy_reg.predict(x_in)


if __name__ == '__main__' :
	## SVR
	x_in, y_in = get_poly_data()
	x = [x_in[i][1] for i in range(len(x_in))]
	y_prd1, y_prd2= svm_poly_prd(x_in, y_in, C = 100), svm_poly_prd(x_in, y_in, C = 20)
	y_prd3, y_prd4 = svm_poly_prd(x_in, y_in, C = 1), svm_poly_prd(x_in, y_in, C = 0.1)

	y_prd5, y_prd6= svm_poly_prd(x_in, y_in, epsilon = 0.1), svm_poly_prd(x_in, y_in, epsilon = 1.0)
	y_prd7, y_prd8= svm_poly_prd(x_in, y_in, epsilon = 5.0), svm_poly_prd(x_in, y_in, epsilon = 10)

	## l_reg
	l_poly_reg = Pipeline([
		('poly_x', PolynomialFeatures()),
		('l_reg', LinearRegression())
	])
	l_poly_reg.fit(x_in, y_in)
	y_prd = l_poly_reg.predict(x_in)
	y_prd_plt = [i[0] for i in y_prd]

	#绘图
	plt.subplot(2,2,1)
	plt_two_prd(x, y_prd1, y_prd), plt.title('C = 100, epsilon = 0.1')
	plt.subplot(2,2,2)
	plt_two_prd(x, y_prd2, y_prd), plt.title('C = 20, epsilon = 0.1')
	plt.subplot(2,2,3)
	plt_two_prd(x, y_prd3, y_prd), plt.title('C = 1, epsilon = 0.1')
	plt.subplot(2,2,4)
	plt_two_prd(x, y_prd4, y_prd), plt.title('C = 0.1, epsilon = 0.1')
	plt.show()

	plt.subplot(2, 2, 1)
	plt_two_prd(x, y_prd5, y_prd), plt.title('C = 100, epsilon = 0.1')
	plt.subplot(2, 2, 2)
	plt_two_prd(x, y_prd6, y_prd), plt.title('C = 100, epsilon = 1.0')
	plt.subplot(2, 2, 3)
	plt_two_prd(x, y_prd7, y_prd), plt.title('C = 100, epsilon = 5.0')
	plt.subplot(2, 2, 4)
	plt_two_prd(x, y_prd8, y_prd), plt.title('C = 100, epsilon = 10')
	plt.show()

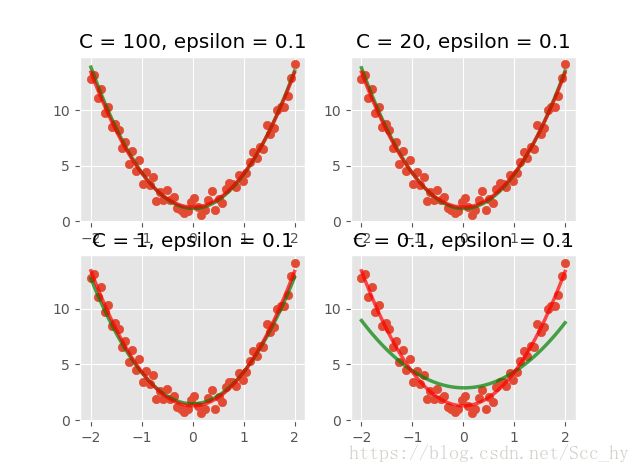
当epsilon = 0.1 时， C 越小（脾气越小）数据容错率越高，模型拟合越随意。 所以在回归任务的时候C 要相对较大。

本质是正则化参数：该参数越大，使用的正则化越少。

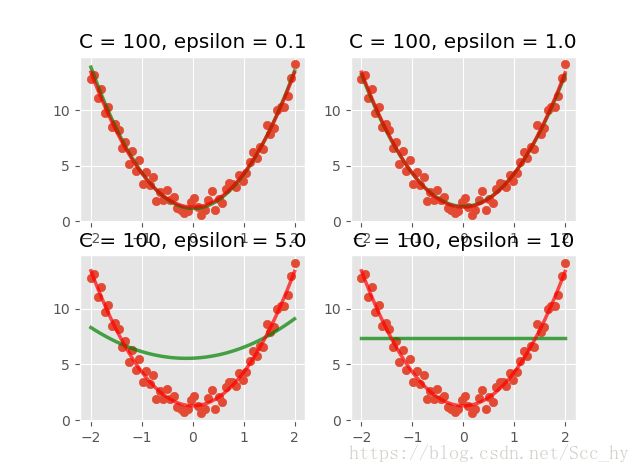
当控制C = 100 即软间隔大小固定的时候， 随着 epsilon 增加，其模型拟合反而更差，这和SVM线性回归不同