ALS推荐算法

在完成基于大数据平台的图书馆推荐系统后，最近把学习的中心放在机器学习上面。在接下来的几个月中，希望自己能弄明白常见机器学习算法的原理，并且能在spark平台上进行实践。

在我的机器学习学习和实践之路的一个本书是《Spark机器学习》，这本书虽然比较旧，但是写的还是比较好。书里讲了各种常见的机器学习算法，并且在spark平台上进行了实战。在学习到此书第四章--构建基于spark的推荐系统引擎时觉得ALS算法在待分析数据具备用户对物品的打分时是一个很好用的算法，所以做记录如下。

推荐系统的产生主要是因为在公司的一些日常业务需求中需要通过用户的一些购买、借阅、点评等记录来准确预测用户下一阶段的类消费倾向以产生更大的经济效益等。在进入大数据时代的今天，数据量巨大，对于企业而言如何构建一个高效的推荐系统来对用户进行个性化一直是一个在研究和改进的问题。推荐系统的系统的核心在于推荐算法，常见的推荐算法有见链接--推荐算法综述，华科大一硕士论文。

ALS中文名作交替最小二乘法，在机器学习中，ALS特指使用最小二乘法求解的一个协同过滤算法，是协同过滤中的一种。ALS算法是2008年以来，用的比较多的协同过滤算法。它已经集成到Spark的Mllib库中，使用起来比较方便。从协同过滤的分类来说，ALS算法属于User-Item CF，也叫做混合CF，因为它同时考虑了User和Item两个方面，即即可基于用户进行推荐又可基于物品进行推荐。

一般而言用户只会购买物品集中的极少数部分产品，并对其进行打分。考虑下面这样一个包含用户的打分矩阵（列为用户u1-u6，行为物品I1-I8），我们可以看到这个用户的评分矩阵是十分稀疏的，有很多用户的购买的记录是空的，而且在现实业务中，用户的评分矩阵会更加的稀疏。如何通过这样一个稀疏矩阵，对用户进行协同推荐用户可能很喜欢的物品对于推荐系统而言是一种很大的考验。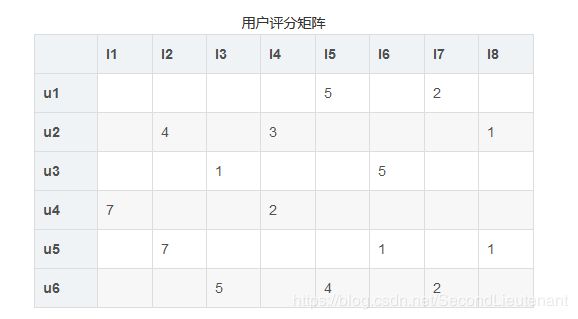

在spark MLlib 机器学习库中目前推荐模型只包含基于矩阵分解(matrix factorization)的实现。具体的分解思路，找出两个低维的矩阵，使得它们的乘积是原始矩阵。因此这也是一种降维技术。假设我们的用户和物品分别是U和I，那对应的“用户-物品”矩阵的维度为U×I，类似图一所示：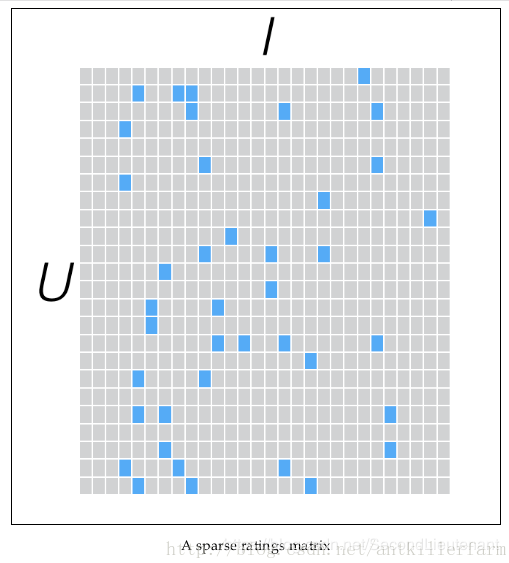

而言找到和“用户-物品“矩阵近似的k维（低阶）矩阵，最终还是要求出如下两个矩阵：一个用于表示用户U×k维矩阵，以及一个表征物品的I×k维矩阵。这两个矩阵也称为因子矩阵，他们的矩阵乘积便是原始评级数据的一个近似值。值得注意的是，原始评级矩阵通常很稀疏，但因子矩阵却是稠密的，如图二所示：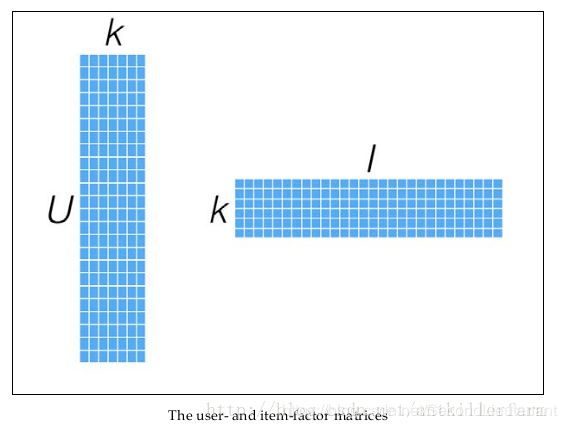

 

ALS是求解矩阵分解问题的一种最优化方法，它功能强大，效果理想而且被证明相对容易实现。这使得它很适合如Spark这样的平台。

ALS的实现原理是迭代式求解一系列最小二乘回归问题。在每次迭代时，固定用户因子矩阵或者是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵。之后，被更新的矩阵被固定住，再更新另外一个矩阵。如此迭代，知道模型收敛（或者是迭代了预设好的次数）。

书中的利用ALS模式实现推荐的代码实例及注释
 

// 加载观众影评数据集（观众ID，影片ID，评分）
val rawData = sc.textFile("dataSet/MLDataSet/u.data")
rawData.first()
val rawRating = rawData.map(_.split("\t").take(3))
 
import  org.apache.spark.mllib.recommendation.ALS
 
import  org.apache.spark.mllib.recommendation.Rating
// 将rawRating由数组类型转换为rating（user,movie,rating）类型
//Rating(user,product,rating)
val rating = rawRating.map{case Array(user,movie,rating)=>Rating(user.toInt,movie.toInt,rating.toDouble)}
//训练模型，rank，iterations，lambda参数值分分别为50,10,0.1.
val model = ALS.train(rating,50,10,0.01)
// 基于用户的推荐
//预测出用户789对123电影的评分
val productRating = model.predict(789,123)
// 返回用户789的前10推荐电影
val userId = 789
val K = 10
val topKRecs = model.recommendProducts(userId,K)
print(topKRecs.mkString("\n"))
// 加载电影数据集（编号，电影名（上映年）....）
val movies = sc.textFile("dataSet/MLDataSet/u.item")
//只取（编号，电影名（上映年）），生成的是一个key->value
val titles = movies.map(line=>line.split("\\|").take(2)).map(array=>(array(0).toInt,array(1))).collectAsMap()
titles(123)
//查看用户789点评过的所有电影
val moviesForUser = rating.keyBy(_.user).lookup(789)
println(moviesForUser.size)
//查看观众点评数据集中评分最高的前10影片并电影编号相应转换成电影名
moviesForUser.sortBy(-_.rating).take(10).map(rating=>(titles(rating.product),rating.rating)).foreach(println)
//返回用户789的前10推荐电影并电影编号相应转换成电影名
topKRecs.map(rating=>(titles(rating.product),rating.rating)).foreach(println)
 
moviesForUser.sortBy(-_.rating).take(10).map(rating=>(titles(rating.product),rating.rating)).foreach(println)
 
//物品推荐
//导入jblas包创建向量
import org.jblas.DoubleMatrix
val aMatrix = new DoubleMatrix(Array(1.0,2.0,3.0))
//定义计算输入量为向量的余弦形式度公式
def consineSimilarity(vec1:DoubleMatrix,vec2:DoubleMatrix):Double={
    vec1.dot(vec2)/(vec1.norm2()*vec2.norm2())
}
 
val itemId = 567
val itemFactor=model.productFeatures.lookup(itemId).head
val itemVector = new DoubleMatrix(itemFactor)
consineSimilarity(itemVector,itemVector)
//计算各个物品的相似度
val sims = model.productFeatures.map{case(id,factor)=>
    val factorVector=new DoubleMatrix(factor)
    val sim = consineSimilarity(factorVector,itemVector)
    (id,sim)
     }
val K = 10
//找到相似度排名前10的
val sortedSims = sims.top(K)(Ordering.by[(Int,Double),Double]{case(id,similarity)=>similarity})
println(sortedSims.take(10).mkString("\n"))
 
println(titles(itemId))
 
val sortedSims2 = sims.top(K+1)(Ordering.by[(Int,Double),Double]{case(id,similarary)=>similarary})
sortedSims2.slice(1,11).map{case (id,sim)=>(titles(id),sim)}.mkString("\n")
//取出user和product
val temp = rating.map{case Rating(user,product,rate)=>(user,product)}
 
 
//推荐结果效果的评定
//MSE均方差
//对于某一特定用户
val actualRating = moviesForUser.take(1)(0)
val predictedRating = model.predict(789,actualRating.product)
val squaredError = math.pow(actualRating.rating-predictedRating,2.0)
//对于全部用户
val usersProducts = rating.map{case Rating(user,product,rating)=>(user,product)}
val predictions = model.predict(usersProducts).map{case Rating(user,product,rating)=>((user,product),rating)}
val ratingsAndPredictions = rating.map{case Rating(user,product,rating)=>((user,product),rating)}.join(predictions)
val MSE =ratingsAndPredictions.map{case((user,product),(actual,predicted))=>math.pow((actual-predicted),2)}.reduce(_+_)/ratingsAndPredictions.count
//均方根差
val RMSE = math.sqrt(MSE)
 
//直接调用Mllib内置函数计算RMSE和MSE
import org.apache.spark.mllib.evaluation.RegressionMetrics
val  predictedAndTrue = ratingsAndPredictions.map{case((user,product),(predicted,actual))=>(predicted,actual)}
val regressionMetrics = new RegressionMetrics(predictedAndTrue)
println("MSE:"+regressionMetrics.meanSquaredError)
println("RMSE:"+regressionMetrics.rootMeanSquaredError)