数据结构与算法-树与二叉树（概念篇）
数据结构与算法-树与二叉树（概念篇）
很长时间没有写关于数据结构的文章了， 那是因为最近实在是太忙了， 而梳理数据结构这方面的知识点又很庞大驳杂，只能尽可能地总结的，压缩。与此同时这又需要很长的准备时间。
树与二叉树决定分两部分，分为概念篇和数据结构算法篇。
我们先来熟悉一下树与二叉树部分相关的概念和结构。
树
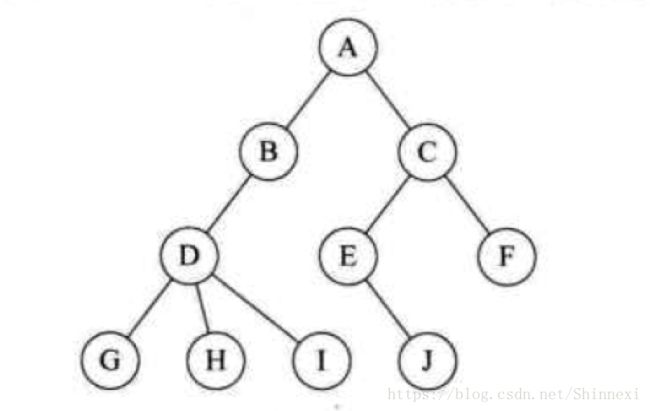
树 是n (n>=0)个结点的有限集合。n=0 时为空树。 在任意一颗非空的树中：1.有且仅有一个特殊成为根Root 的结点；2. 当n>1时， 其余结点又可以分为m>0个互不想交的有限集，T1，T2,T3,,,,Tm, 其中每一有限集又是一棵树，并且称为根的子树 SubTree
节点的度
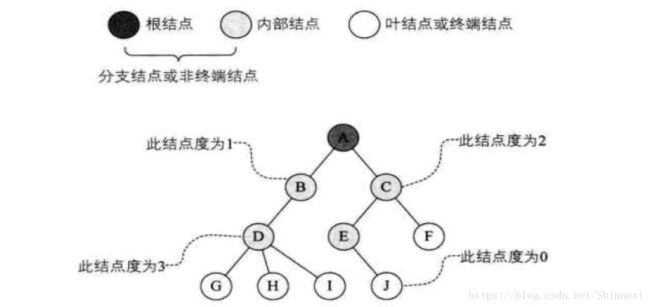
结点拥有的子树数称为结点的度。度为0的结点称为叶子结点或终端结点，度不为0的结点称为非终端结点或分支结点。除根结点以外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。
层次与深度
节点的层次 level 从根节点开始定义起，根为第一层，根的孩子为第二层。 若某节点在第I层，则其子树的根就在第I+1层。 其双亲在同一层的节点互为堂兄弟。
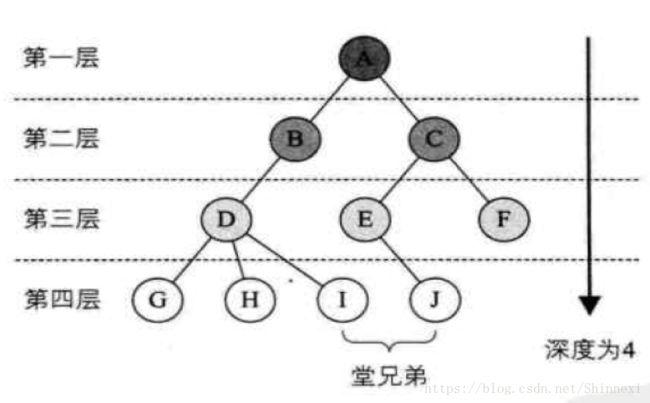
树中节点的最大层次成为树的深度 depth 或者高度。
有序树和无序树
如果将树中节点的各子树看成从左至右是有次序的，不能互换的，则称为该树为有序树，否则为无序树。
森林
森林是M >=0 个不想交的树的集合
树的存储结构
看过我前几篇数据解析的都知道，线性表和hash表的数据结构。但是对于树的存储，很显然
简单的顺序存储不能满足树的实现 而且需要结合顺序存储和链式存储来实现。
树的存储结构 常用三种表示方法。
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
双亲表示法
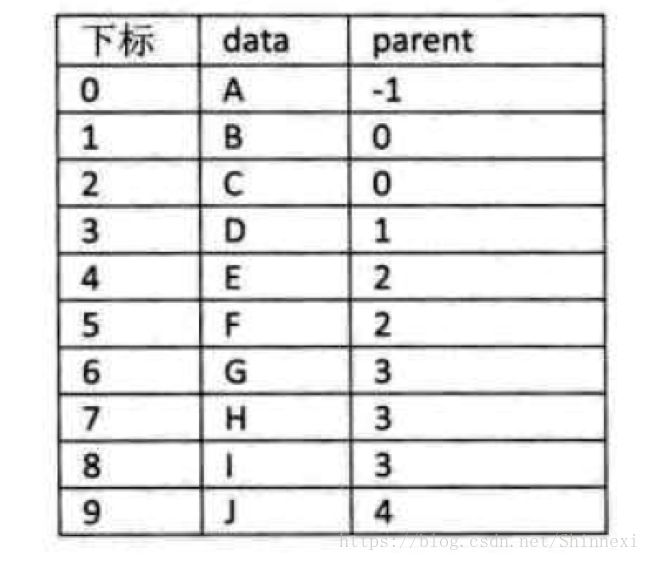
在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。
data- parent
每个节点只记录自己的父节点即可。
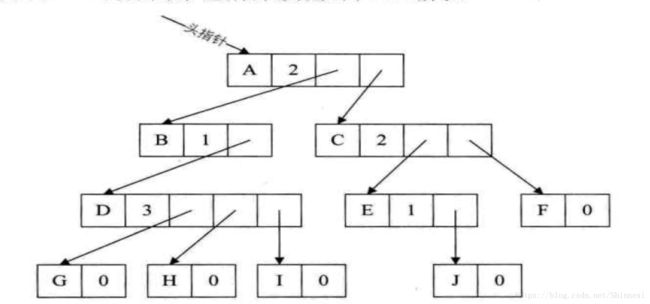
孩子表示法
data- left_child - right_child
每个节点记录自己的两个孩子， 左孩子与右孩子。
方法1.
方法2.
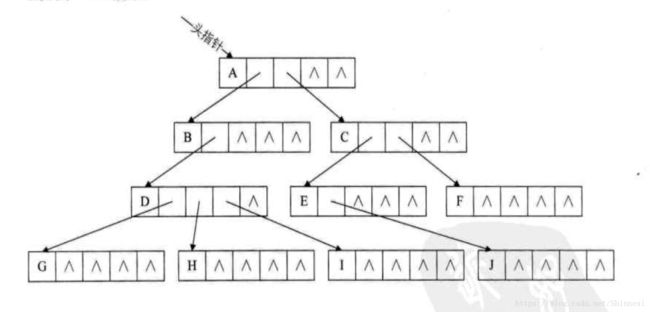
孩子兄弟表示法
data-firstchild-rightslib
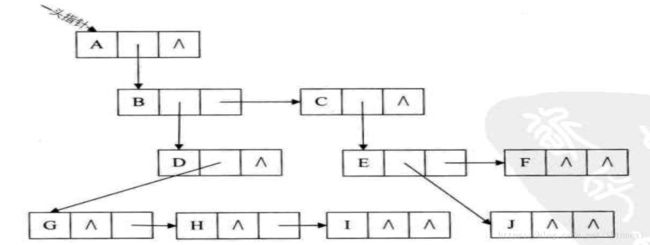
任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟
二叉树
二叉树（binary tree） 是 n（n>=0) 个节点的有限集合，该集合或者空集称为空二叉树， 或者由一个根节点和两颗互不想交的、分别称为根节点的左子树和右子树的二叉树组成。
特殊二叉树
斜二叉树
所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树
其实这种树，想想看是不是和链表很一样。
满二叉树
在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树成为满二叉树。
完全二叉树
对于一颗具有n个节点的二叉树按照层序编号，如果编号为i（1<=i<=n)的节点与同样深度的满二叉树中编号为IDE节点在二叉树中位置完全相同，则这可二叉树成为完全二叉树。
二叉树的性质总结
这一部分是照搬课本的， 也不必死记硬背。 就是根据性质来就行了。
- 1：在二叉树的第i层上至多有2i-1个结点（i>=1）。
- 2：深度为k的二叉树至多有2k-1个结点（k>=1）。
- 3：对任何一颗二叉树T，如果其终端结点数为n0,度为2的 结点 数为n2，则n0 = n2+1.
- 4：具有n个结点的完全二叉树深度为[log2n]+1 ([x]表示不 大于 x的最大整数)。
- 5：如果对一颗有n个结点的完全二叉树（其深度为[log2n]+1） 的结点按层序编号（从第1层到第[log2n]+1层，每层从左到 右），对任意一个结点i(1<=i<=n)有:
- a. 如果i=1,则结点i是二叉树的根，无双亲；如果i>1,则其双亲是结点[i/2]
- b. 如果2i>n,则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i。
- c. 如果2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+1。
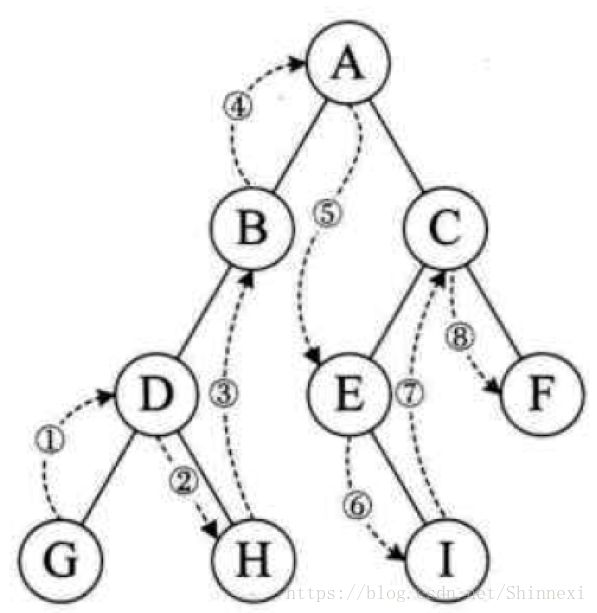
二叉树的遍历
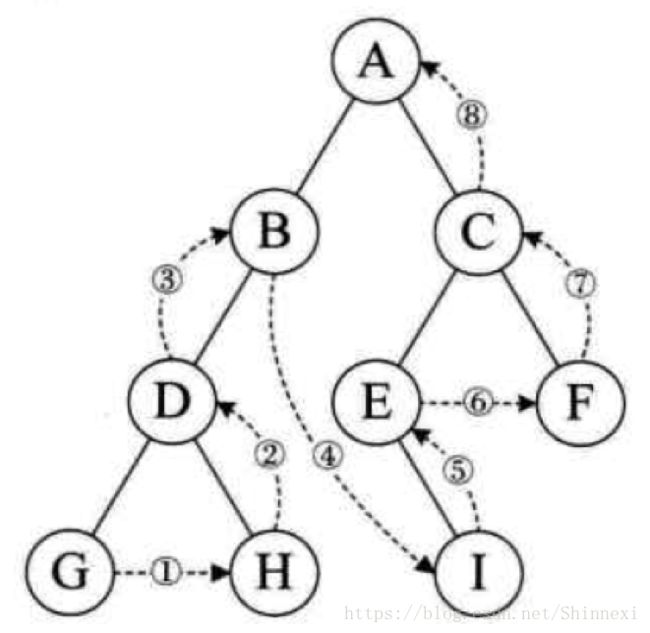
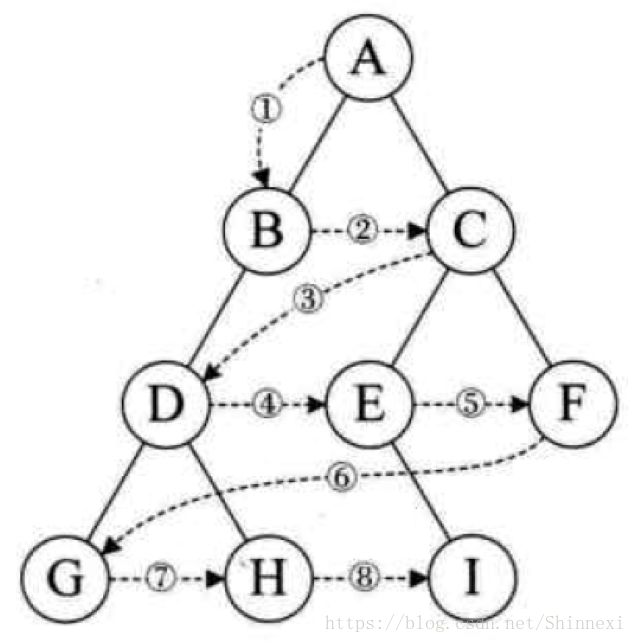
前序遍历
规则是若二叉树为空，则空操作返回，否则先访问跟结点，然后前序遍历左子树，再前序遍历右子树
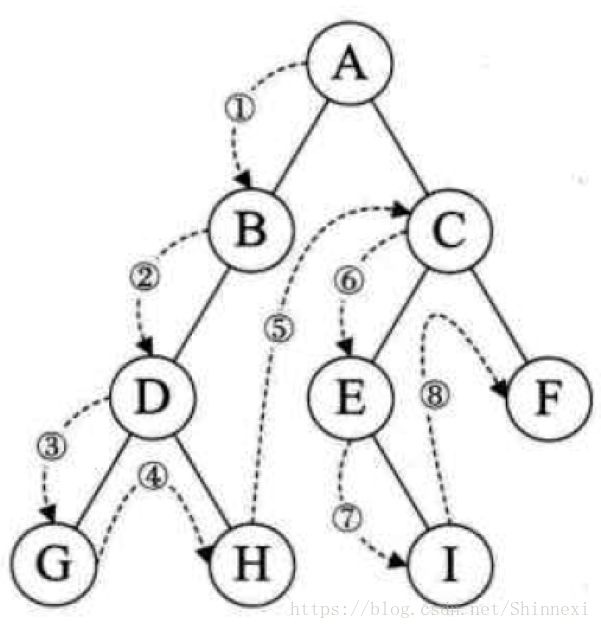
中序遍历
规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树
后序遍历
规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点
层序遍历
规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层，按从左到右的顺序对结点逐个访问
树、 森林、 二叉树的转换
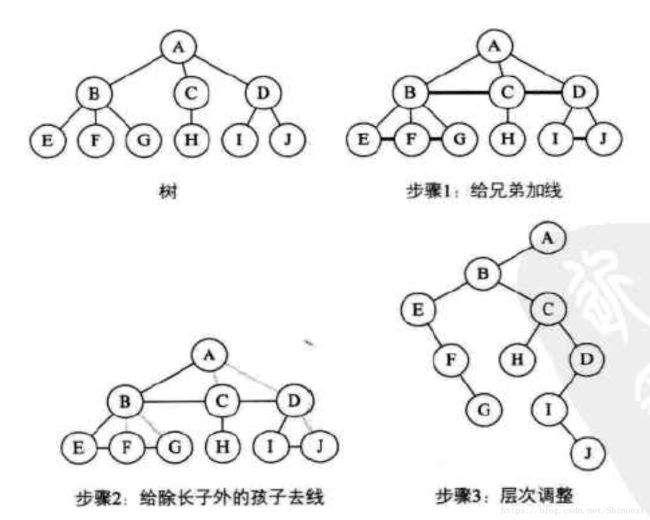
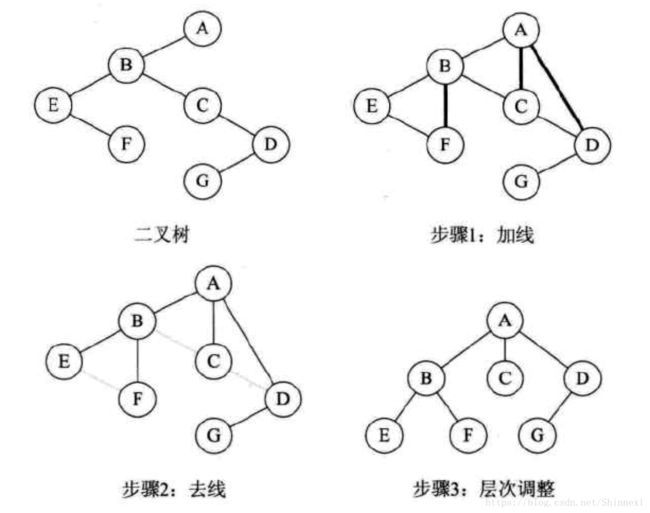
树转换为二叉树
- 加线。在所有兄弟节点之间加一条线。
- 去线。对树中每个节点，只保留它与第一个孩子节点的连线，删除它与其他孩子节点之间的连线。
- 层次调整。 以树的根节点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。注意第一个孩子是二叉树节点的左孩子，兄弟转换过来的孩子是节点的右孩子。
森林转换为二叉树
- 把每个树转换为二叉树
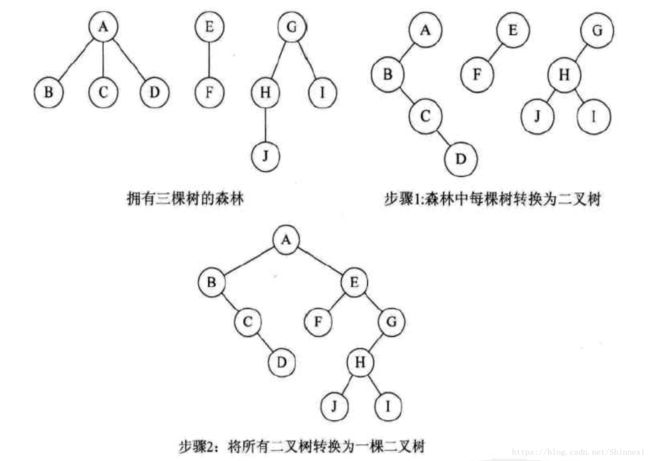
- 第一棵二叉树不动，从第二课二叉树开始，依次把后一颗二叉树的根节点作为前一棵二叉树根节点的右孩子，用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。
二叉树转换为树
- 加线。若某节点的左孩子节点存在，则将这个左孩子的右孩子节点、右孩子的右孩子节点、右孩子的右孩子的右孩子节点。。。n个右孩子节点都作为此节点的孩子。将该节点与这些右孩子节点用线连接起来。
- 去线。删除原二叉树中所有节点与其右孩子节点的连线。
- 层次调整。 使之结构层次分明。
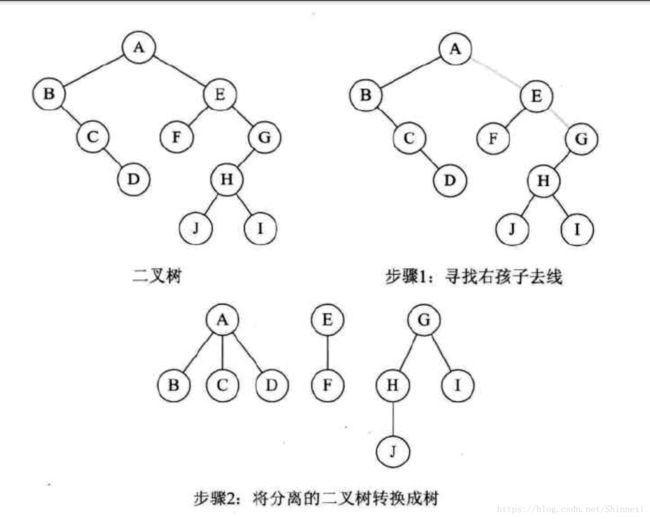
二叉树转森林
判断一颗二叉树能不能转换成一颗树还是森林，就只要看这个二叉树的根节点有没有右孩子，有就是森林，没有就是一棵树。转换步骤。
1. 从根节点开始，若右孩子存在，则把与右孩子连接的线删除，再查看分离后的二叉树，若右孩子存在，则连线删除。。。。，直到所有右孩子连线都删除为止，得到分离的二叉树。
2. 再将每颗分离后的二叉树转换为树即可。
赫夫曼树
给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
赫夫曼树的构建
二叉查找树（BST）
- 左子树上所有结点的值均小于或等于它的根结点的值。
- 右子树上所有结点的值均大于或等于它的根结点的值。
- 左、右子树也分别为二叉排序树。
红黑树（Black Red Tree）
红黑树是一种自平衡的二叉查找树。
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点（NIL节点）。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
红黑树的自平衡部分牵涉到很多情况，这里就先不说了。下一篇文章会结合Java 中的TreeMap 进行详细分析红黑树部分算法。
总结
数据结构这部分的确很多复杂的东西。这一部分仅仅是部分概念部分，记录下来算是复习吧， 如果有不对的地方，欢迎批评指正。
参考链接
赫夫曼树的构建
维基百科-红黑树