kaggle比赛记录——ieee_fraud_detection问题
文章目录
- 题目
- 简单尝试版
- 0. 所需python包
- 1. 数据
- 1.1 导入数据并显示
- 1.2 分析数据
- 2. 岭回归
- 2.1 学习曲线
- 2.2 岭回归模型
- 2.3 数据预处理:样本不平衡
- 2.4 数据预处理:把类别太多的特征用factories处理
- 3. LightBGM模型
- 3.1 超参数调参顺序及范围(Classifier)
- 3.1.1 max_depth = np.arange(3, 10, 2)和num_leaves = np.arange(50, 170, 30)
- 3.1.2 'min_child_samples':[18, 19, 20, 21, 22],'min_child_weight':[0.001, 0.002, 0.003]
- 3.1.3 subsample = np.arange(0.5, 1, 0.1), subsample_freq = np.arange(1, 6, 1)
- 3.1.4 reg_alpha = [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5] reg_lambda = [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5]
- 3.1.5 learning_rate = [0.005, 0.01, 0.1, 0.3] n_estimators = [1000, 1200, 1500, 2000, 2500]
- 3.2 岭回归和lgbm融合结果
- 3.3 使用所有数据lgbm结果
- 3.4 数据预处理:缺失值处理
- 3.5 数据预处理2:缺失值处理(用算法填补)
- 4. 聚类分析
- 4.1 考虑特征addr1、addr2、dist1、dist2
- 4.2 考虑特征addr1、addr2
- 5. 逻辑回归
- 5.1 数据预处理:标准化处理
- 5.2 逻辑回归
- 6 全部数据(题目给的两个文件的数据)
- 7 提交
- 进阶探索版
- 1 特征选择
- 2 利用全部数据
- 3 利用全部(两个文件)数据(最终的即包括测试阶段不可见数据)
题目
题目链接:https://www.kaggle.com/c/ieee-fraud-detection/data
数据集:
简单尝试版
0. 所需python包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBClassifier
from xgboost import XGBRegressor
import sklearn.metrics as metrics
from sklearn.model_selection import train_test_split, GridSearchCV, learning_curve
import lightgbm as lgbm
1. 数据
1.1 导入数据并显示
def input_dataset(train_data_path):
print('====================数据:导入及显示数据====================')
train_transaction = pd.read_csv(train_data_path, index_col=0)
# train_identity = pd.read_csv('dataset/train_identity.csv', index_col=0)
pd.set_option('display.max_columns', None) # 显示最大列
pd.set_option('display.max_rows', None) # 显示最大行
pd.set_option('expand_frame_repr', False) # 每一行不分行显示
train_transaction_fraud = train_transaction[train_transaction['isFraud'] == 1]
print(train_transaction.head(10))
print(train_transaction_fraud.head(10))
print('总样本与欺诈样本数: ', len(train_transaction), ' ', len(train_transaction_fraud))
return train_transaction
1.2 分析数据
def anaysis_data(train_transaction):
print('====================分析:ProductCD与是否欺诈的关系====================')
print(train_transaction.groupby(['ProductCD', 'isFraud'])['isFraud'].count())
print(train_transaction[['ProductCD', 'isFraud']].groupby(['ProductCD']).mean())
train_transaction[['ProductCD', 'isFraud']].groupby(['ProductCD']).mean().plot.bar()
print('====================分析:card4:支付方式与是否欺诈的关系====================')
print(train_transaction.groupby(['card4', 'isFraud'])['isFraud'].count())
print(train_transaction[['card4', 'isFraud']].groupby(['card4']).mean())
train_transaction[['card4', 'isFraud']].groupby(['card4']).mean().plot.bar()
print('====================分析:card6:卡的类别与是否欺诈的关系====================')
print(train_transaction.groupby(['card6', 'isFraud'])['isFraud'].count())
print(train_transaction[['card6', 'isFraud']].groupby(['card6']).mean())
train_transaction[['card6', 'isFraud']].groupby(['card6']).mean().plot.bar()
print('====================分析:P_emaildomain:支付邮箱与是否欺诈的关系====================')
print(train_transaction.groupby(['P_emaildomain', 'isFraud'])['isFraud'].count())
print(train_transaction[['P_emaildomain', 'isFraud']].groupby(['P_emaildomain']).mean())
train_transaction[['P_emaildomain', 'isFraud']].groupby(['P_emaildomain']).mean().plot.bar()
print('====================分析:R_emaildomain:支付邮箱与是否欺诈的关系====================')
print(train_transaction.groupby(['R_emaildomain', 'isFraud'])['isFraud'].count())
print(train_transaction[['R_emaildomain', 'isFraud']].groupby(['R_emaildomain']).mean())
train_transaction[['R_emaildomain', 'isFraud']].groupby(['R_emaildomain']).mean().plot.bar()
plt.show()
2. 岭回归
尝试用岭回归处理分类问题,注意网格搜索超参数时在评分标准上改变。
但是是简单版本,对于个别变量做个尝试。
2.1 学习曲线
# 学习曲线
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5), verbose=0):
"""
Generate a simple plot of the test and training learning curve.
Parameters
-------------
estimator:object type that implents the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title:string
Title for the chart.
X:array-like,shape(n_samples,n_features)
Training vector,where n_samples is the number of samples and n_features is
the number of features.
y:array-like,shape(n_samples) or (n_samples,n_features),optional
Target relative to X for classification or regression;
None for unsupervised learning.
ylim:tuple,shape(ymin,ymax),optional
Defines minimum and maximum yvalues plotted.
cv:integer,cross-validation generator,optional
If an integer is passed,it is the number of folds(defaults to 3).
Specific cross-validation objects can be passed,see
sklearn.cross_validation module for the list of possible objects
n_jobs:integer,optional
Number of jobs to run in parallel(default 1).
"""
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv,
n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1, color='r')
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color='g')
plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
plt.legend(loc="best")
plt.show()
return plt
2.2 岭回归模型
def deal_dataset(train_transaction):
print('====================处理:对训练数据和测试数据one-hot编码====================')
train_transaction_y = train_transaction.pop('isFraud')
predictors = ['ProductCD', 'card4', 'card6', 'P_emaildomain', 'R_emaildomain']
train_transaction = train_transaction[predictors]
print(train_transaction.head(50))
# colsMean = train_transaction.median()
# train_transaction.fillna(colsMean)
# print(train_transaction.isnull().sum().sum())
train_transaction_dummies = pd.get_dummies(train_transaction)
X_train, X_test, y_train, y_test = train_test_split(train_transaction_dummies, train_transaction_y, test_size=0.3)
print('====================搭建模型:岭回归====================')
# 网格搜索最佳超参数
ridge = Ridge()
alphas = np.array([1.5, 1.7, 1.9, 2, 2.1, 2.3])
parameters = [{'alpha': alphas}]
grid_search = GridSearchCV(estimator=ridge, param_grid=parameters, scoring='roc_auc', cv=10, verbose=10)
result = grid_search.fit(X_train, y_train)
best = grid_search.best_score_
best_parameter = grid_search.best_params_
print('Ridge result: ', result)
print('best_score: ', best)
print('best_parameter: ', best_parameter)
best_alpha = best_parameter['alpha'] # 获取best参数
ridge = Ridge(alpha=best_alpha) # 设置岭回归参数
ridge.fit(X_train, y_train)
y_pre_ridge = ridge.predict(X_test) # 岭回归预测结果
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pre_ridge, pos_label=1)
auc_ridge = metrics.auc(fpr, tpr)
print('岭回归的auc分数为:', auc_ridge)
print(X_train.shape[0])
plot_learning_curve(ridge, 'ridge_curve', X_train, y_train, cv=10, verbose=10)
最后结果:
Ridge result: GridSearchCV(cv=10, error_score='raise',
estimator=Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'alpha': array([1.5, 1.7, 1.9, 2. , 2.1, 2.3])}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=10)
best_score: 0.7433455792394993
best_parameter: {'alpha': 1.5}
岭回归的auc分数为: 0.7399430645824021
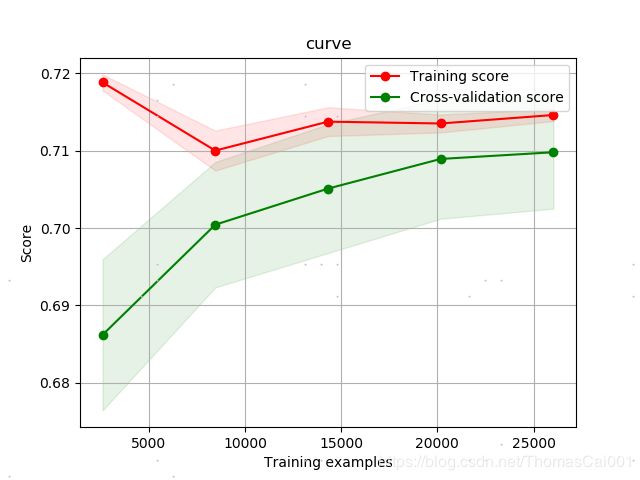
学习曲线:
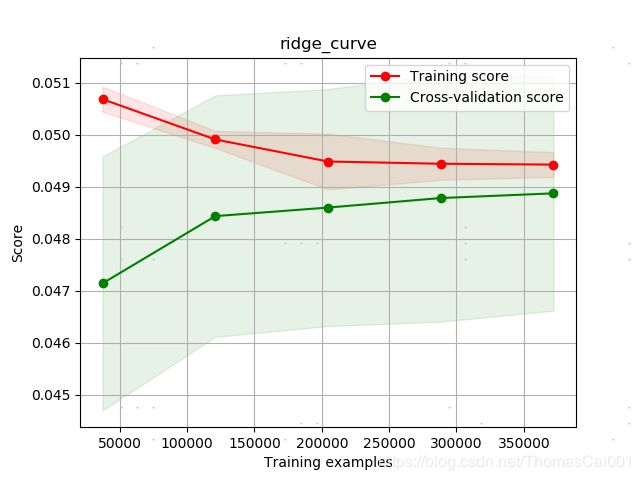
结论:从学习曲线可以看出,最后的得分是很低的,当然暴露的问题也有很多:
- 数据集正负样本不平均肯定是个很大的问题(isFraud|0:569877, 1:20663),准备先采取随机采样0类与1类大致相同的样本,然后继续。最后可用bagging的思想进行集成学习;
- 其次的问题肯定在数据集上,邮箱的种类太多不宜用dummies可以用factories去数字化字符串值,对于如此多的特征,特征选择也是很重要的。可以尝试各种特征选择的方法;
- 在特征选择之前,可以尝试地再分析特征与目标变量的关系,特征之间相关性的分析,特征变量的正规化;
- 最后用模型,调参数,得到最后结果。
2.3 数据预处理:样本不平衡
在上述的基础上,随机取与负样本同样数量的正样本(诚信样本),进行同样的实验,实验结果如下。
Ridge result: GridSearchCV(cv=10, error_score='raise',
estimator=Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'alpha': array([1.5, 1.7, 1.9, 2. , 2.1, 2.3])}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=10)
best_score: 0.7495973469607634
best_parameter: {'alpha': 1.5}
岭回归的auc分数为: 0.7406929216448217
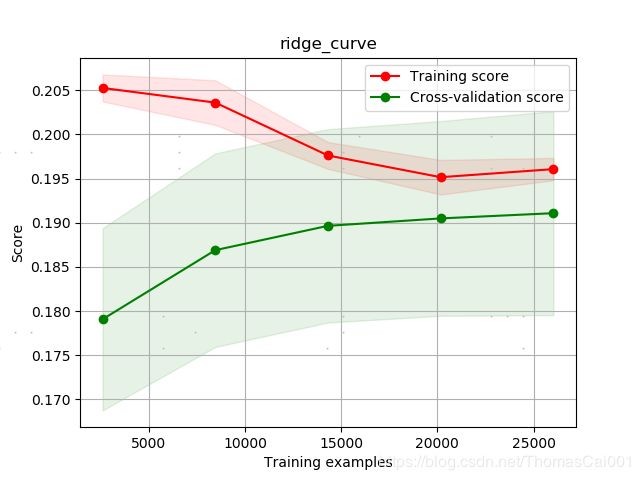
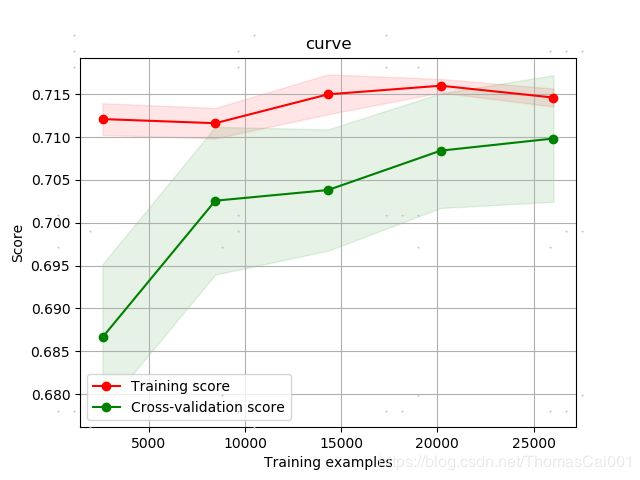
小结:可以看出,对样本采样处理样本不平衡问题对结果有不错的提升,但可以说是才到达可以训练效果的地步。
2.4 数据预处理:把类别太多的特征用factories处理
在上述的基础上,对于
R_emaildomain和P_emaildomain特征,由于他们类别太多,这里用pd.factories处理成索引表示特征,而不会像get_dummies一样把该列铺开。
Ridge result: GridSearchCV(cv=10, error_score='raise',
estimator=Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'alpha': array([1.5, 1.7, 1.9, 2. , 2.1, 2.3])}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=10)
best_score: 0.7285821039391717
best_parameter: {'alpha': 1.7}
岭回归的auc分数为: 0.7303458823259997
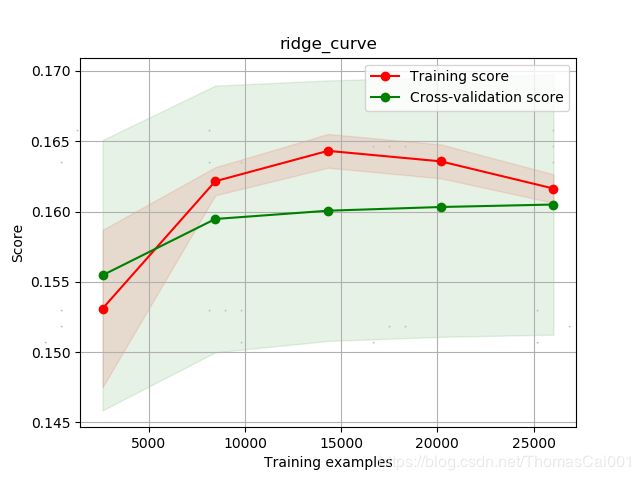
小结:但从实验结果来看,效果并没有get_dummies好…
3. LightBGM模型
3.1 超参数调参顺序及范围(Classifier)
参考:
https://blog.csdn.net/weixin_41370083/article/details/79276887
https://www.cnblogs.com/bjwu/p/9307344.html
(1)n_estimators和learning_rate:
params = {
'boosting_type': 'gbdt',
'objective': 'regression',
'learning_rate': 0.1,
'num_leaves': 50,
'max_depth': 6,
'subsample': 0.8,
'colsample_bytree': 0.8,
}
‘n_estimators’:[100,200,500,1000,1500]
(2)max_depth和num_leaves :
max_depth = np.arange(3, 10, 2)
num_leaves = np.arange(50, 170, 30)
(3)min_child_samples和 min_child_weight:
‘min_child_samples’:[18, 19, 20, 21, 22],
‘min_child_weight’:[0.001, 0.002, 0.003]
(4)subsample 和 subsample_freq:
subsample = np.arange(0.5, 1, 0.1)
subsample_freq = np.arange(1, 6, 1)
(6)正则化参数调优:
‘reg_alpha’: [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5],
‘reg_lambda’: [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5]
(7)进一步 降低学习速率 增加更多的树:
‘learning_rate’:[0.005, 0.01,0.1,0.3]
‘learning_rate’: 0.1 不变
‘n_estimators’:[1000,1200,1500,2000,2500]
‘n_estimators’: 2000 较好
3.1.1 max_depth = np.arange(3, 10, 2)和num_leaves = np.arange(50, 170, 30)
result: GridSearchCV(cv=5, error_score='raise',
estimator=LGBMClassifier(boosting_type='gbdt', class_weight=None, colsample_bytree=1.0,
importance_type='split', learning_rate=0.1, max_depth=-1,
min_child_samples=20, min_child_weight=0.001, min_split_gain=0.0,
n_estimators=100, n_jobs=-1, num_leaves=31, objective=None,
random_state=None, reg_alpha=0.0, reg_lambda=0.0, silent=True,
subsample=1.0, subsample_for_bin=200000, subsample_freq=0),
fit_params=None, iid=True, n_jobs=4,
param_grid=[{'max_depth': array([3, 5, 7, 9]), 'num_leaves': array([ 50, 80, 110, 140])}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=1)
best_score: 0.7601702110841377
best_parameter: {'max_depth': 9, 'num_leaves': 80}
lgb的auc分数为: 0.7619433417100694
max_depth = np.array([7, 8, 9])
num_leaves = np.array([68,74,80,86,92])
best_score: 0.7601048100561123
best_parameter: {'max_depth': 8, 'num_leaves': 74}
lgb的auc分数为: 0.7600162799802694
3.1.2 ‘min_child_samples’:[18, 19, 20, 21, 22],‘min_child_weight’:[0.001, 0.002, 0.003]
best_score: 0.7644900411718537
best_parameter: {'min_child_samples': 19, 'min_child_weight': 0.001}
lgb的auc分数为: 0.7540527797250189
3.1.3 subsample = np.arange(0.5, 1, 0.1), subsample_freq = np.arange(1, 6, 1)
best_score: 0.7623175995286935
best_parameter: {'subsample': 0.8999999999999999, 'subsample_freq': 1}
lgb的auc分数为: 0.7581324437105174
3.1.4 reg_alpha = [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5] reg_lambda = [0, 0.001, 0.01, 0.03, 0.08, 0.3, 0.5]
best_score: 0.7583165909174154
best_parameter: {'reg_alpha': 0.08, 'reg_lambda': 0.03}
lgb的auc分数为: 0.7641478728781967
3.1.5 learning_rate = [0.005, 0.01, 0.1, 0.3] n_estimators = [1000, 1200, 1500, 2000, 2500]
这也是这一系列调参的最后一步,换句话说,此也为最终的调参结果。
best_score: 0.7600250133938856
best_parameter: {'learning_rate': 0.1, 'n_estimators': 1000}
lgb的auc分数为: 0.7695625808160469
3.2 岭回归和lgbm融合结果
y_hat = (y_pre_ridge + y_pre_lgb)/2
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_hat, pos_label=1)
auc = metrics.auc(fpr, tpr)
print('岭回归和lgb的auc分数为:', auc)
岭回归和lgb的auc分数为: 0.754521684209069
从融合的结果可以看出,岭回归和lgbm融合后结果并不理想,原因也很好想,岭回归拉低了分数,从单岭回归就可知岭回归效果不好。因此以下尝试用逻辑回归。
3.3 使用所有数据lgbm结果
2.2 岭回归模型中的代码片段中,选取了部分特征,用于岭回归,因为岭回归不能处理缺失字段,但lgbm可以,所以这里屏蔽掉选取部分特征的代码。
def deal_dataset(train_transaction):
print('====================处理:对训练数据和测试数据one-hot编码====================')
train_transaction_y = train_transaction.pop('isFraud')
# predictors = ['ProductCD', 'card4', 'card6', 'P_emaildomain', 'R_emaildomain']
# train_transaction = train_transaction[predictors]
print(train_transaction.head(50))
lgb部分代码:
print('================搭建模型:lgbm==================')
parameter_init_lgb = {'max_depth': 8, 'num_leaves': 74, 'min_child_samples': 19, 'min_child_weight': 0.001,
'subsample': 0.9, 'subsample_freq': 1, 'reg_alpha': 0.08, 'reg_lambda': 0.03,
'learning_rate': 0.1, 'n_estimators': 1000}
lgb = lgbm.LGBMClassifier(**parameter_init_lgb)
lgb.fit(X_train, y_train)
y_pre_lgb = lgb.predict(X_test)
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pre_lgb, pos_label=1)
auc = metrics.auc(fpr, tpr)
print('lgb的auc分数为:', auc)
结果:
lgb的auc分数为: 0.8962334630751195
非常吃惊,用所有特征居然有这么大的提升,还想到其实还有一个文件的特征没用,随后可以考虑用,在此之前,我这里先处理下缺失数据。
3.4 数据预处理:缺失值处理
数值特征用中位数填补,非数值特征用众数填补。
train_transaction_object = train_transaction.columns[train_transaction.dtypes == 'object']
train_transaction_math = train_transaction.columns[train_transaction.dtypes != 'object']
train_transaction.fillna(train_transaction[train_transaction_math].median(), inplace=True)
train_transaction.fillna(train_transaction[train_transaction_object].mode().iloc[0], inplace=True)
结果:
best_parameter: {‘alpha’: 2.3}
岭回归的auc分数为: 0.8530467234218518
lgb的auc分数为: 0.8905115734749858
岭回归和lgb的auc分数为: 0.9258773953110936
3.5 数据预处理2:缺失值处理(用算法填补)
- 用随机森林预测值填补
def fillna_value_way3_rf(train_transaction, fillna_df, feature_name):
card2_df_dummies = pd.get_dummies(fillna_df)
card2_df_notnull = card2_df_dummies.loc[(train_transaction[feature_name].notnull())]
card2_df_isnull = card2_df_dummies.loc[(train_transaction[feature_name].isnull())]
X = card2_df_notnull.values[:, 1:]
Y = card2_df_notnull.values[:, 0]
# use RandomForestRegression to train data
RFR = RandomForestRegressor(n_estimators=1000, n_jobs=-1)
RFR.fit(X, Y)
predictcard2 = RFR.predict(card2_df_isnull.values[:, 1:])
train_transaction.loc[train_transaction[feature_name].isnull(), [feature_name]] = predictcard2
card2_df = train_transaction[['card2', 'TransactionDT', 'TransactionAmt', 'ProductCD', 'card1', 'card4', 'card6', 'P_emaildomain', 'R_emaildomain']]
card3_df = train_transaction[['card3', 'TransactionDT', 'TransactionAmt', 'ProductCD', 'card1', 'card4', 'card6', 'P_emaildomain', 'R_emaildomain']]
card5_df = train_transaction[['card5', 'TransactionDT', 'TransactionAmt', 'ProductCD', 'card1', 'card4', 'card6', 'P_emaildomain', 'R_emaildomain']]
fillna_value_way3_rf(train_transaction, card2_df, 'card2')
fillna_value_way3_rf(train_transaction, card3_df, 'card3')
fillna_value_way3_rf(train_transaction, card5_df, 'card5')
结果:
best_parameter: {‘alpha’: 2.3}
岭回归的auc分数为: 0.8569801503386929
lgb的auc分数为: 0.8889994095511866
岭回归和lgb的auc分数为: 0.9225397465163611
- 用岭回归预测值填补
ridge = Ridge(alpha=2.3) # 设置岭回归参数
ridge.fit(X, Y)
predictcard2 = ridge.predict(card2_df_isnull.values[:, 1:])
结果:
岭回归的auc分数为: 0.8500008952044523
lgb的auc分数为: 0.8925319806585874
岭回归和lgb的auc分数为: 0.9205296560416307
小结: 这样看来,用预测值去填充不会比中位数填充有较大的提升,甚至还比不过后者的auc分数。
4. 聚类分析
4.1 考虑特征addr1、addr2、dist1、dist2
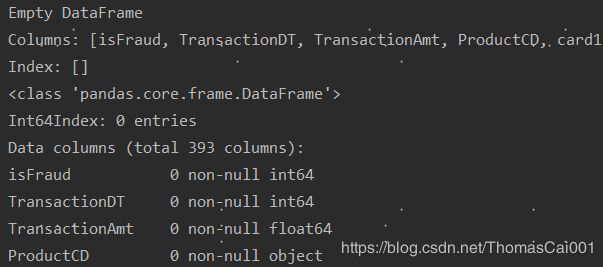
对于这四个特征,分别可理解为交易的ip地址,交易所到账户的ip地址,分析发现,特征dist1和dist2缺失值较多,多到不存在这两个特征同时有值的样本…
这里先把显示表信息用一个函数写起来:show_basis_info.py
import pandas as pd
def show_basis_info(train_transaction, n):
pd.set_option('display.max_columns', None) # 显示最大列
pd.set_option('display.max_rows', None) # 显示最大行
pd.set_option('expand_frame_repr', False) # 每一行不分行显示
print(train_transaction.head(n))
print(train_transaction.info(verbose=True, null_counts=True))
然后查询dist1和dist2均不为空的字表:
import pandas as pd
from show_basis_info import show_basis_info
train_data_path = 'dataset/train_transaction.csv'
train_transaction = pd.read_csv(train_data_path, index_col=0)
train_transaction_dist1 = train_transaction.loc[train_transaction['dist1'].notnull()]
train_transaction_dist2 = train_transaction_dist1.loc[train_transaction['dist2'].notnull()]
show_basis_info(train_transaction_dist2, 5)
4.2 考虑特征addr1、addr2
绘制的所有样本数(addr1、addr2均有值):524834
其中欺诈样本数:511912
其中非欺诈样本数:12922
代码如下:(中间注释部分是将欺诈样本和非欺诈样本分别先存入表中,这是由于机器内存不足。。。尴尬,本来可以直接处理的。)
train_transaction_not_path = 'dataset/train_transaction_not.csv'
train_transaction_is_path = 'dataset/train_transaction_is.csv'
train_transaction_not = pd.read_csv(train_transaction_not_path, index_col=0)
train_transaction_is = pd.read_csv(train_transaction_is_path, index_col=0)
# train_transaction_not = train_transaction.loc[train_transaction['isFraud'] == 0]
# train_transaction_is = train_transaction.loc[train_transaction['isFraud'] == 1]
# train_transaction_not.to_csv('dataset/train_transaction_not.csv')
# train_transaction_is.to_csv('dataset/train_transaction_is.csv')
# train_transaction_address = train_transaction[['addr1', 'addr2', 'dist1', 'dist2']]
# show_basis_info(train_transaction_not, 5)
# train_transaction_address.fillna(0, inplace=True)
img1 = train_transaction_not.plot.scatter(x='addr1', y='addr2', color='r', label='notFraud')
train_transaction_is.plot.scatter(x='addr1', y='addr2', color='b', label='isFraud', ax=img1) # , ax=img1
plt.xlabel('location_x')
plt.ylabel('location_y')
plt.title('train_transaction addr location analysis')
plt.show()
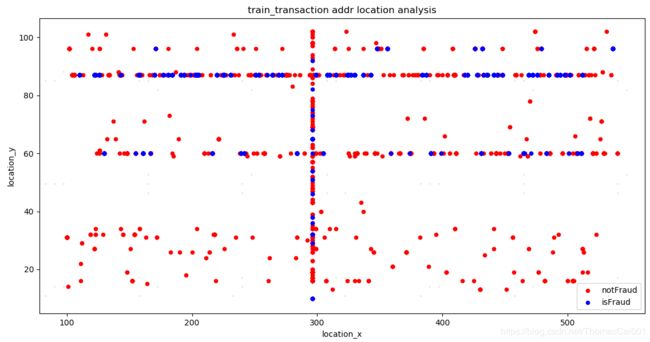
图中看出,蓝色的欺诈位置还是很有规律的,大多数集中在一条线上,与非欺诈样本鱼目混杂,这里想到一种利用这个结果的方法(以下Fx、Fy对应addr1和addr2):
- 分别计算出欺诈样本的位置,Fx和Fy;
- 计算Fx和Fy的所有样本数,并得到欺诈样本分别在Fx和Fy的比例:Px和Py;
- 对于最后测试样本的Fx和Fy位置的最后预测结果分别加上Px和Py,增强在这两个位置为欺诈样本的可信度;
5. 逻辑回归
此连接第3部分,用逻辑回归再进行一次实验。
5.1 数据预处理:标准化处理
由于岭回归和lgbm不需要标准化处理,因此在这里进行处理。
详细证明: https://blog.csdn.net/shwan_ma/article/details/80154888
但,标准化处理有助于迭代过程中,目标函数的收敛,以下结果岭回归和lgbm仍然用了标准化处理,从结果也可以得出上述的结论。
print('====================数据预处理:标准化处理所有x====================')
num_columns = train_transaction_dummie.columns[train_transaction_dummie.dtypes != object]
sc = StandardScaler()
sc.fit(train_transaction_dummie.loc[:, num_columns])
train_transaction_dummie.loc[:, num_columns] = sc.transform(train_transaction_dummie.loc[:, num_columns])
show_basis_info(train_transaction_dummie, 5)
X_train, X_test, y_train, y_test = train_test_split(train_transaction_dummie, train_transaction_y, test_size=0.3)
5.2 逻辑回归
print('================搭建模型:逻辑回归==================')
lr = LogisticRegression(C=1.0, tol=0.01)
lr.fit(X_train, y_train)
y_pre_lr = lr.predict(X_test)
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pre_lr, pos_label=1)
auc = metrics.auc(fpr, tpr)
print('lr的auc分数为:', auc)
结果:
岭回归的auc分数为: 0.8538645117826613
lgb的auc分数为: 0.8928569086487236
岭回归和lgb的auc分数为: 0.9224198403468866
lr的auc分数为: 0.7817860900601115
6 全部数据(题目给的两个文件的数据)
# 导入另一个数据集
train_identity = pd.read_csv('dataset/train_identity.csv', index_col=0)
train_transaction = pd.concat((train_transaction, train_identity), axis=1)
Ridge result: GridSearchCV(cv=10, error_score='raise-deprecating',
estimator=Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001),
fit_params=None, iid='warn', n_jobs=None,
param_grid=[{'alpha': array([1.5, 1.7, 1.9, 2. , 2.1, 2.3])}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring='roc_auc', verbose=10)
best_score: 0.8611331225822505
best_parameter: {'alpha': 1.5}
岭回归的auc分数为: 0.8658265220675434
================搭建模型:lgbm==================
lgb的auc分数为: 0.8976235417666026
岭回归和lgb的auc分数为: 0.9279946771566198
================搭建模型:逻辑回归==================
lr的auc分数为: 0.7894110269427566
7 提交
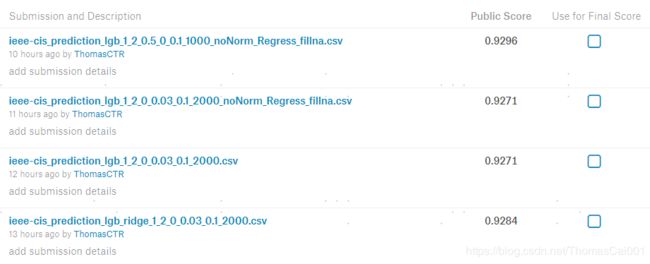
到这里,我想用刚刚这个所有数据的结果提交,结果跑测试程序的时候提示内存错误,尴尬。因此,这里还是仅用一个文件来做分类,最后的结果并不是很理想,结果如下:

最高的排名:

这边带raw字样的是用lgbm原始数据结果得到的,最后的排名着实悲伤,不过也可以理解,毕竟没做什么数据预处理,数据都没用全,本来还以为得到0.90+湛湛自喜,以为走了捷径,没成想科学没有捷径- - ok,继续该进。
如今可以想到的改进方法:
- 特征选择
- 利用全部数据(两个文件)
- 利用部分特征(如聚类结果)
进阶探索版
1 特征选择
- 1.首先尝试lgbm内的特征选择(用L2正则化,用错了…下面还会有L1范式)
reg_alpha : float, optional (default=0.) L1 regularization term on weights.
reg_lambda : float, optional (default=0.) L2 regularization term on weights.
- 置’reg_alpha’: 0, 搜索到’reg_lambda’: 0.03
- 再搜索:
earning_rate = [0.005, 0.01, 0.1, 0.3] # 0.1
n_estimators = [1000, 1200, 1500, 2000, 2500] # 1000
best_score: 0.9522322981775311
best_parameter: {'learning_rate': 0.1, 'n_estimators': 2000}
lgb的auc分数为: 0.9507343936470288
- 2.仍然是lgbm内的特征选择(L1正则化来进行特征选择)
- 置’reg_lambda’: 0, 搜索到’reg_alpha’: 0.5
best_score: 0.9266414127250973
best_parameter: {'reg_alpha': 0.5}
lgb的auc分数为: 0.9305030668236514
- 再搜索:
earning_rate = [0.005, 0.01, 0.1, 0.3] # 0.1
n_estimators = [1000, 1200, 1500, 2000, 2500] # 1000
best_score: 0.9496253003031797
best_parameter: {'learning_rate': 0.1, 'n_estimators': 1000}
lgb的auc分数为: 0.9524031447523469
- 3.L1正则化后用lgb_raw data测试一遍
best_parameter: {'alpha': 1.5}
岭回归的auc分数为: 0.852853132309268
lgb的auc分数为: 0.9576021072551657
岭回归和lgb的auc分数为: 0.9570399019029211
2 利用全部数据
- 这里仍然用1中的特征选择最佳表现的组合L1正则化+两个模型融合
- 这里的全部数据仍然是第一个文件
- 但是对于负样本(诚信)进行多次采样(26次 - 相差倍数),对最后的分类结果取均值。
测试代码片
y_hat_res, y_ridge_res, y_lgb_res = 0, 0, 0
for i in range(1, 27):
print('==========第', i, '/27'+'轮ing=========')
train_transaction_deal = balance_p_n_samples(train_transaction) # 处理样本不平衡的问题
train_transaction_y = train_transaction_deal.pop('isFraud')
whole_data = pd.concat((train_transaction_deal, test_transaction), axis=0)
whole_data = preprocess(whole_data, 'regress')
y_pre_ridge, y_pre_lgb, y_hat = deal_dataset2(whole_data, train_transaction_deal, train_transaction_y, test_transaction)
y_hat_res = (y_hat_res + y_hat) / i
y_ridge_res = (y_ridge_res + y_pre_ridge) / i
y_lgb_res = (y_lgb_res + y_pre_lgb) / i
# 保存最后数据
submission_df = pd.DataFrame(data={'TransactionID': test_transaction.index, 'isFraud': y_hat_res})
submission_df.to_csv('classify_result/ieee-cis_prediction_lgb_ridge_1_2_0.5_0_0.1_1000_regress_fillna_noNorm_26.csv',
index=False)
submission_df = pd.DataFrame(data={'TransactionID': test_transaction.index, 'isFraud': y_ridge_res})
submission_df.to_csv('classify_result/ieee-cis_prediction_ridge_1_2_0.5_0_0.1_1000_regress_fillna_noNorm_26.csv',
index=False)
submission_df = pd.DataFrame(data={'TransactionID': test_transaction.index, 'isFraud': y_lgb_res})
submission_df.to_csv('classify_result/ieee-cis_prediction_lgb_1_2_0.5_0_0.1_1000_regress_fillna_noNorm_26.csv',
index=False)
3 利用全部(两个文件)数据(最终的即包括测试阶段不可见数据)
以上就是初次参加kaggle的思考以及实现流程,最后成绩也是非常的糟,4429/6381。不过这次我前后用的时间不长是事实,而且更多的还是去摸索数据分析的流程,看了其他的赛后总结,我发觉我真是缺乏很多的思考,具体表现如下:
- 对于原始的数据,我缺乏对于数据本身的分析;
- 仍然是数据分析方面,并没有实际上应用特征选择。
参考:
[1] https://tianchi.aliyun.com/notebook-ai/detail?spm=5176.12282042.0.0.1dce20429Jt3oQ&postId=6772
[2] https://www.zybuluo.com/jk88876594/note/802632