贪心算法
什么是贪心算法
贪心算法是一种对某些求解最优问题的更为简单的方法。贪心算法每次都考虑一个局部最优解,总是考虑当前状态下的最优的选择。所以贪心算法并不是对每个问题都有最优解的,但是某些问题,比如单源最短路径,最小生成树问题。(关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关)
贪心算法的基本要素
- 贪心选择:所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到,这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。贪心选择是采用从顶向下、以迭代的方法做出相继选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题。
通常可以首先证明问题的一个整体最优解,是从贪心选择开始的,而且作了贪心选择后,原问题简化为一个规模更小的类似子问题。然后,用数学归纳法证明,通过每一步贪心选择,最终可得到问题的一个整体最优解
- 最优子结构,当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法或动态规划算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响,而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择,不能回退;动态规划则会根据以前的选择结果对当前进行选择,有回退功能。动态规划主要运用于二维或三维问题,而贪心一般是一维问题。
基本思想
-
建立数学模型来描述问题;
-
把求解的问题分成若干个子问题;
-
对每一子问题求解,得到子问题的局部最优解;
-
把子问题的解局部最优解合成原来解问题的一个解。
贪心算法使用实例一 活动安排问题
问题描述:
一天有n个活动,每个活动都在同一个礼堂;同一时间内只能举行一个活动;每个活动 i 都有一个起始时间si和结束时间 fi;
现给定 n 个活动的开始时间和结束时间,请设计一个活动安排,使安排的活动个数最多。
输入 11(活动数)
1 0 3 3 5 5 6 2 8 8 12
4 6 5 8 7 9 10 13 11 12 14
思路:
分析这个问题,有三种容易想到的策略:
- 选择开始时间最早的
- 选择结束时间最早的
- 选择持续时间最短的
那么使用哪一种最好的:
分析第一种,开始时间最早;如果这个活动虽然开始时间最早,但是它从持续时间长怎么办?
分析第三种,如果所有一个持续时间短的活动它刚好搭在了某个活动的结尾和另一个活动的开头?
分析第三种,第三种算法是一种是给未安排的活动尽可能多的时间
总结:利用贪心算法有三步
- 这个题是不是能用贪心算法
- 找出所有贪心的方式,去排除一些明显不可行的贪心方式
- 对可行的贪心方式,进行代码求解
本题伪码:
##
# 先将活动按结束时间排序
# 从最先结束的活动开始,以结束时间为优先排除冲突贪心选择
n = int(input()) # 总的活动数量
start = [int(x) for x in input().split("")] # 所有活动的开始时间列表
end = [int(x) for x in input().split("")] # 所有活动的结束时间列表
# 以 活动序号 和 start 和 end 建立字典联系 // 因为以结束时间排序,字典本身无序,所以结束时间是键
'''
# 先把 start 和 end 联合成 元组单元 start_end = [(a,b), (a,b), (a,b)... ]
start_end = [];
for i in range(n):
start_end.append((start[i],end[i]))
# 将列表 变成以序号为键 的 字典 用到的语法:dict.fromkeys(iterable[,value=None])
dict_message = dict.fromkeys(list(range(1,n+1)),start_end)
'''
num_start = []
for i in range(n):
num_start .append((i+1, start[i]))
dict_message = dict.fromkeys(end,start_end)
# 字典以值排序
sorted_keys = sort(dict_message.keys())
# 以排好的结束时间 为键 查找满足贪心的活动
before_over_time = -1 # 初始化结束时间
selected_actives = []
for key in sorted_keys:
# 如果后一个活动开始时间>=前一个活动的结束时间 活动入选
if( dict_message[key][1]>= before_over_time ):
selected_actives.append(key)
before_over_time = selected_actives[-1] # 入选活动后更新结束时间
print(len(selected_actives )) # 打印入选活动的个数
贪心算法使用实例二 小数背包问题
问题描述:
n种物品和一个背包,物品i重量是wi;价值是Vi;背包的容量是C;可以选择 i 物品的一部分;让包内的价值最大?
输入:
3 50 (物品总数,背包容量)
10 20 30 (物品重量)
60 100 120 (物品价格)
问题分析:
策略一:在不超出背包剩余容量的前提下,选择价值最大的商品
策略二:在不超出背包生于容量的前提下,选择重量最轻的商品
策略三:在不超过剩余容量的前提下,选择价值率最大的商品
策略三满足,可以使用贪心算法。
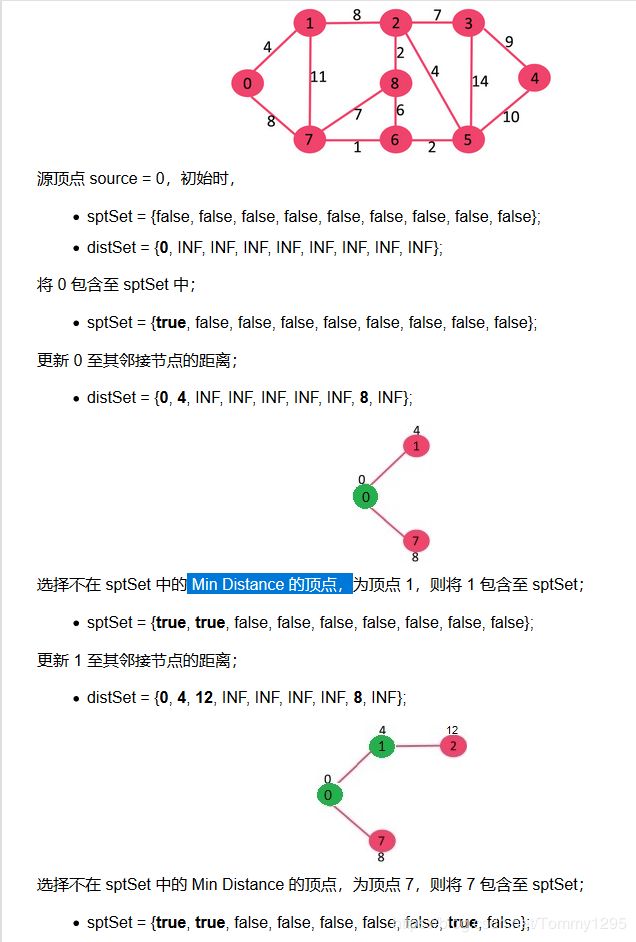
贪心算法使用实例三 单源最短路径
题目描述:给定一个带权有向图G=(V,E),其中每条边的权是一个实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。
本题伪码
定义两个空列表:1.加入点的列表 add_point 2. 起始点到其他点的距离 start_dist
第一轮迭代:
将起始点加入 add_point = [1,0,0,0,0,0,0,0,0,0,0,0,0,0]
更新起始点到相邻的点的距离 start_dist = [0,4,inf,inf,inf,inf,inf,8,inf,inf,]
第二轮迭代:
将不在 add_point 的最小 start_dist 的点加入 add_point 。add_point = [1,1,0,0,0,0,0,0,0,0,0,0,0,0]
更新起始点到相邻点的距离 start_dist = [0,4, 4+8
第三轮迭代:
......
知道add_point 全为1为止。
实现代码
#输入数据
# 5
'''
-1 10 -1 30 100
-1 -1 50 -1 -1
-1 -1 -1 -1 10
-1 -1 20 -1 60
-1 -1 -1 -1 -1
'''
# 将输入数组转换成矩阵的查找形式
n = int(input()) # 表示输入的节点数
neig_rect = [] # 初始化邻接矩阵
for i in range(n):
neig_rect.append([int(x) for x in input().split(" ")]) # 将行输入作为矩阵当单元
# 定义两个初始列表记录数据
add_point = [0]*n
inf = float("inf")
start_dist = [inf]*n
# 第一次迭代 比如说第一个点是源点
add_point[0] = 1 # 加入源点 初始加入点由题目指定
for i ,j in enumerate (neig_rect[0]): # 检查源点到所有相邻点 *
if j>0:
start_dist[i] =min(start_dist[i], j) # 更新源点到其他点的距离
start_dist[0] = 0 # 源点到源点的距离为0
# 第2.... n 次迭代
while sum(add_point)0:
start_dist[i] =min(start_dist[i],minest[0]+ j) # 更新源点到其他点的距离
print("路径总和是",sum(start_dist)) 最小生成树---Prim算法
单源最短路径是考虑某个点到其余点的最短路径之和。
最小生成树是考虑连接所有点的最短路径。(单源最短路径和最小生成路径不是一回事)
输入:
6
0
6 0
1 5 0
5 -1 5 0
-1 3 6 -1 0
-1 -1 4 2 6 0伪代码:
# 维护两个 list[] 一个用来表示点到点的开销1,另一个表示 访问标记2
加入任意点
更新这个点到其他点的距离,挑出最小的边的点
加入这个点 (在访问标记list2中做好标记)
更新这个点到其他点的距离,较小的可以替换,另外不要与已经访问的点做比较
实现代码:
# 6
# 0
# 6 0
# 1 5 0
# 5 -1 5 0
# -1 3 6 -1 0
# -1 -1 4 2 6 0
# 分析输入 数据,第一行数字代表 图中所有的点数
# 列的元素序号 代表着每个点的序号;值代表着序号为i(i是列号)的点到该点的距离 为了更好的利用向量,需要将输入作为矩阵转置
import numpy as np
n = int(input())
rect_array_in = np.zeros((n, n), "int32")
for i in range(n):
in_line = [int(x) for x in input().split(" ")]
rect_array_in[i, 0:len(in_line)] = in_line # 将下三角矩阵 输入np.array
# 转置
rect_array_in_1 = rect_array_in.T
# 合成对称矩阵
rect_array_in_3 = rect_array_in+rect_array_in_1
print(rect_array_in_3)
# 维护: 一个指定点到其他点之间的最小距离矩阵 一个点访问标记矩阵
add_point = [0]*n # 访问矩阵
inf = float("inf")
start_dist = [inf]*n # 距离矩阵
# 第一次迭代
first_1 = 0 # 先指定初始点
add_point[0] = 1
minest = [0, inf] # 序号和值
for i, j in enumerate(list(rect_array_in_3[first_1])): # 遍历指定点到其余点的距离
if j >= 0: # 更新距离表
start_dist[i] = min(j, start_dist[i])
print("赋值形况", start_dist[i])
if add_point[i] != 1 and start_dist[i] < minest[1]: # 取下最小的点
minest[1] = start_dist[i]
minest[0] = i
print("第二次加入的点", minest[0]+1,start_dist ) #加入点的序号是
# 后续迭代
add_point[minest[0]] = 1 # 加入该点
while sum(add_point) < n:
print("加入的点 状态", minest[0], add_point)
minest[1] = inf # 序号和值
for i, j in enumerate(list(rect_array_in_3[minest[0]])): # 遍历指定点到其余点的距离
if add_point[i] != 1 and j >= 0: # 更新距离表
start_dist[i] = min(j, start_dist[i])
for i, j in enumerate(start_dist):
if start_dist[i] <= minest[1] and add_point[i] == 0: # 取下最小的点
minest[1] = start_dist[i]
minest[0] = i
print("状态是", i)
add_point[minest[0]] = 1 # 加入该点
print("最小生成树的路径长度是", sum(start_dist))
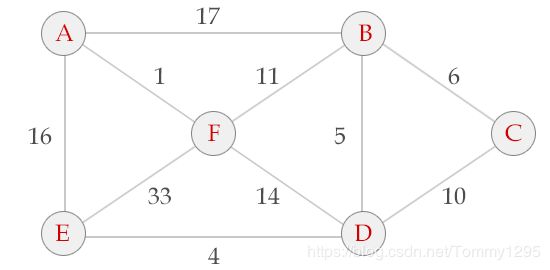
Kruskal 算法
Kruskal算法基本思想:
(1) 将全部边按照权值由小到大排序。
(2) 按顺序(边权由小到大的顺序)考虑每条边,只要这条边和我们已经选择的边不构成圈,就保留这条边,否则放弃这条边。
算法 成功选择(n-1)条边后,形成一棵最小生成树,当然如果算法无法选择出(n-1)条边,则说明原图不连通
实现代码:
输入:
6 (所有点的个数)
0
17 0
-1 6 0
-1 5 10 0
16 -1 -1 4 0
1 11 -1 33 0
实现代码
"""
6
0
17 0
-1 6 0
-1 5 10 0
16 -1 -1 4 0
1 11 -1 14 33 0
"""
# 首先
# 结合算法的基本思路
# 确定将数据输入的格式做如何调整
# 本题是要对每个边的长度大小进行排序,所以以边为主,边需要和两个端点关联
# 读取输入的每一行 将每一行的边长端点信息用 [边长 端点序号 端点序号] 表示
n = int(input())
edge_inf = []
for i1, i in enumerate(range(n)):
in_line = [int(x) for x in input().split(" ")]
for j1, j in enumerate(in_line):
if j > 0:
x = [j, i1, j1]
edge_inf.append(x)
# 得到了边长信息之后,排序 ,再去比较 并选出可用的边
print("所有边长数据", edge_inf)
def take_first(elem):
return elem[0]
edge_inf.sort(key=take_first)
print("排序后边长数据", edge_inf)
# 不要形成封闭的圆形,每次挑选最短
# 用集合的知识
set_1 = set()
ans = []
for ii in edge_inf:
if ii[1] not in set_1 or ii[2] not in set_1:
ans.append(ii[0])
set_1 = set_1 | set(ii[1:])
print("最后选出的结果是:", ans)
最优前缀码
现在给定字符集和每个字符出现的频次;请设计算法构造其最优前缀码
输入
6(字符的个数)
45 13 12 16 9 5
输出:
2.2400 (最优前缀码的平均码长,保留4位小数)
基本思路:(哈夫曼思想:把出现频率高的用较短的码,频率出现低的用较长的码)
将频次放在最小堆中
每次取出堆中最小的节点,然后去构造森林,最后这个遍历这个森林的每片叶子,就是最优前缀码。
代码实现: