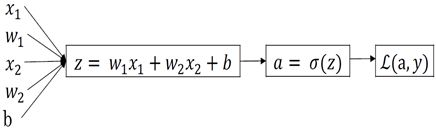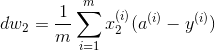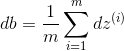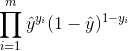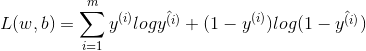吴恩达Deeplearning.ai之1-2:神经网络基础
这段时间看了吴恩达老师的deeplearning.ai课程,为了以后回顾相关知识点,特此做了课程的笔记。笔记按照吴恩达老师的教学视频的章节进行记录。这篇笔记是关于神经网络基础的,主要内容如下:
目录
1. 二分类(Binary Classification):
2. 逻辑回归(Logistic Regression):
3. 逻辑回归的代价函数(Logistic Regression cost fuction):
4. 梯度下降法(Gradient Descent):
5. 逻辑回归中的梯度下降(Logistic Regression Gradient Descent):
6. m个样本的梯度下降(Gradient descent on m examples):
7. 向量化(Vectorization):
8. 向量化逻辑回归(Vectorizing Logistic Regression):
9. 逻辑回归代价函数的解释(Explanation of logistic regression cost function):
1. 二分类(Binary Classification):
给定特征向量(矩阵)![]() ,预测输出标签
,预测输出标签![]() 是
是![]() 还是
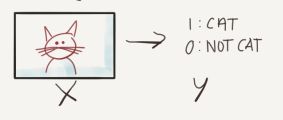
还是![]() 的分类,称作二分类。比如输入一张动物的图片,判断这张图片中的动物是否是猫,若是猫,输出
的分类,称作二分类。比如输入一张动物的图片,判断这张图片中的动物是否是猫,若是猫,输出![]() ,若不是猫,输出
,若不是猫,输出![]() 。
。
这就是典型的二分类问题。在本小节中,吴恩达老师主要讲解了几个Notation,如下:
样本:![]() ,其中
,其中![]() 。
。![]() 属于
属于![]() 维空间,表示样本
维空间,表示样本![]() 有
有![]() 个特征,
个特征,![]() 表示
表示![]() 标签
标签
样本集:![]() ,表示样本集中有
,表示样本集中有![]() 个样本
个样本
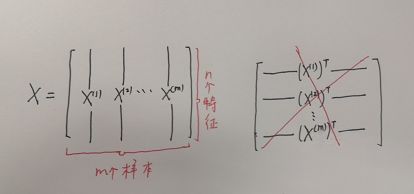
在神经网络中,输入(特征)矩阵![]() 是按行堆叠而不是按列堆叠的,即输入矩阵
是按行堆叠而不是按列堆叠的,即输入矩阵![]() 如下所示:
如下所示:
显然,输入矩阵![]() 的形状为
的形状为 ![]() ,在python中可以用语句
,在python中可以用语句![]() 来查看矩阵
来查看矩阵![]() 的维度。输出标签向量
的维度。输出标签向量![]() 的表示如下:
的表示如下:
![]()
输出标签向量![]() 的形状为
的形状为![]() ,同样可以用语句
,同样可以用语句![]() 来查看向量
来查看向量![]() 的维度。
的维度。
2. 逻辑回归(Logistic Regression):
逻辑回归是常见的二分类模型,它的输出不是具体的![]() 标签,而是一个概率,即
标签,而是一个概率,即![]() 之间的一个数值,比如说,我想要用逻辑回归预测明天是不是要下雨,它的输出是明天下雨的概率,而不是{下雨,不下雨}。想要让预测输出的值在
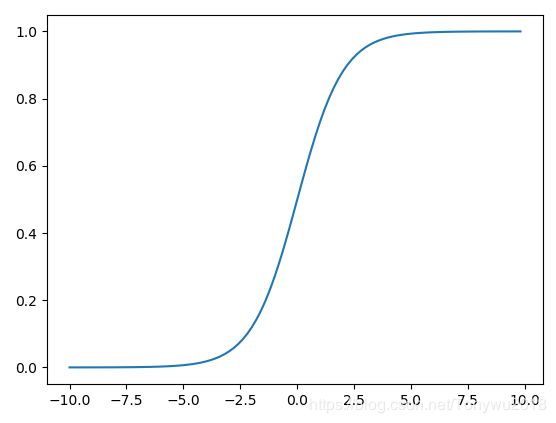
之间的一个数值,比如说,我想要用逻辑回归预测明天是不是要下雨,它的输出是明天下雨的概率,而不是{下雨,不下雨}。想要让预测输出的值在![]() ,引入了Sigmoid函数,它的函数图像如下:
,引入了Sigmoid函数,它的函数图像如下:
于是就有:
![]()
从Sigmoid的函数表达式以及函数图像可以看到,当自变量![]() 是正无穷是,输出无限接近
是正无穷是,输出无限接近![]() ;当自变量
;当自变量![]() 是负无穷时,输出无限接近于
是负无穷时,输出无限接近于![]() ,当自变量
,当自变量![]() 为
为![]() 时,输出为
时,输出为![]() 。这样,Sigmoid函数把定义域在
。这样,Sigmoid函数把定义域在![]() 的数映射到值域
的数映射到值域![]() 上。
上。
Sigmoid函数的一阶导数是经常考察的问题,它的一阶导数是它本身的函数,即:
![]()
可以看到,当![]() 与
与![]() 相等时,
相等时,![]() 的值最大,即当
的值最大,即当![]() 时,一阶导数
时,一阶导数![]() 取得最大值
取得最大值![]() ,导数为原函数的
,导数为原函数的![]() 倍,随着迭代次数的上升,
倍,随着迭代次数的上升,![]() 越来越小,最终接近于
越来越小,最终接近于![]() ,最终产生梯度消失的现象。
,最终产生梯度消失的现象。
3. 逻辑回归的代价函数(Logistic Regression cost fuction):
给定样本集![]() ,我们想让预测值
,我们想让预测值![]() 尽量接近实际值
尽量接近实际值![]() ,即
,即![]() 。那么我们需要一个损失函数来度量
。那么我们需要一个损失函数来度量![]() 和
和![]() 之间的差值,在线性回归中,我们通常使用平方误差来作为损失函数,即:
之间的差值,在线性回归中,我们通常使用平方误差来作为损失函数,即:
但是在逻辑回归中通常不使用平方误差作为损失函数,这是因为平方误差函数是非凸函数,在用梯度下降进行优化时,一般会得到局部最优解而不是全局最优解。因此在逻辑回归中一般使用交叉熵作为损失函数,如下:
![]()
这样逻辑回归的优化问题就变成了凸优化问题,通过梯度下降可以得到全局最优解。而我们建模训练的目的就是找到一组参数使得损失函数![]() 最小。但是损失函数是针对单样本点。对于全集多样本点,我们需要定义代价函数,即对所有样本点的损失函数求和取平均,如下:
最小。但是损失函数是针对单样本点。对于全集多样本点,我们需要定义代价函数,即对所有样本点的损失函数求和取平均,如下:
可以看到,代价函数![]() 是参数
是参数![]() 的函数,而我们就是要求得一组能够使代价函数最小的参数。那么怎么去求解呢,需要用到梯度下降的优化算法。
的函数,而我们就是要求得一组能够使代价函数最小的参数。那么怎么去求解呢,需要用到梯度下降的优化算法。
4. 梯度下降法(Gradient Descent):
梯度是机器学习中非常重要的概念,我们在高数中对梯度的定义是这样的:设函数![]() 在平面区域D内具有一阶连续偏导数,则对每一点
在平面区域D内具有一阶连续偏导数,则对每一点![]() 都可以定出一个向量
都可以定出一个向量![]() 称为
称为![]() 在P点处的梯度,记作
在P点处的梯度,记作![]() 。梯度的负方向是函数下降最快的方向。用一张比较经典的图片来描述梯度下降:
。梯度的负方向是函数下降最快的方向。用一张比较经典的图片来描述梯度下降:
在曲面上随机找一个初始点,沿着这个初始点向下走(类比于下山的过程),直到走到最低位置处。上图中由于![]() 是非凸函数,所以最终会达到多个局部最优点,如上图中的两条路径。
是非凸函数,所以最终会达到多个局部最优点,如上图中的两条路径。
梯度下降法是常用的最小化代价函数的方法,并可迭代求得使得代价函数最小的参数![]() 。每次迭代式如下:
。每次迭代式如下:
其中![]() 符号表示更新,
符号表示更新,![]() 为学习速率,取值在
为学习速率,取值在![]() 之间。在程序编写中,常用
之间。在程序编写中,常用![]() 表示
表示![]() ,用
,用![]() 表示
表示![]() 。那么梯度下降为什么可以求得函数的最小值呢?
。那么梯度下降为什么可以求得函数的最小值呢?
5. 逻辑回归中的梯度下降(Logistic Regression Gradient Descent):
对于单个样本,有以下定义:
![]()
![]()
![]()
假设样本有![]() 个特征,那么逻辑回归计算图如下图:
个特征,那么逻辑回归计算图如下图:
反向传播:
得到了![]() 后就可以进行梯度下降了:
后就可以进行梯度下降了:
![]()
![]()
![]()
这样就完成了一次迭代。
6. m个样本的梯度下降(Gradient descent on m examples):
对于![]() 个样本,有以下定义:
个样本,有以下定义:
![]()
![]()
同样假设各个样本都只有![]() 个特征,那么各个参数的偏导数也可以写成各个样本点求和取平均的形式:
个特征,那么各个参数的偏导数也可以写成各个样本点求和取平均的形式:
在程序实现中,我们可以使用两个![]() 循环对所有的样本进行一次梯度下降,其中外循环表示样本数,内循环表示每个样本的特征数。但是
循环对所有的样本进行一次梯度下降,其中外循环表示样本数,内循环表示每个样本的特征数。但是![]() 循环的时间复杂度太高,不适合用于数据量巨大的深度学习,这就引入了向量化。
循环的时间复杂度太高,不适合用于数据量巨大的深度学习,这就引入了向量化。
7. 向量化(Vectorization):
若对含有![]() 个样本的数据集向量化会得到:
个样本的数据集向量化会得到:
特征(输入)矩阵![]() :
:![]()
参数向量![]() :
:![]()
偏置![]() :
:![]()
输出向量![]() :
:![]()
那么![]() 个样本的线性输出为:
个样本的线性输出为: ![]()
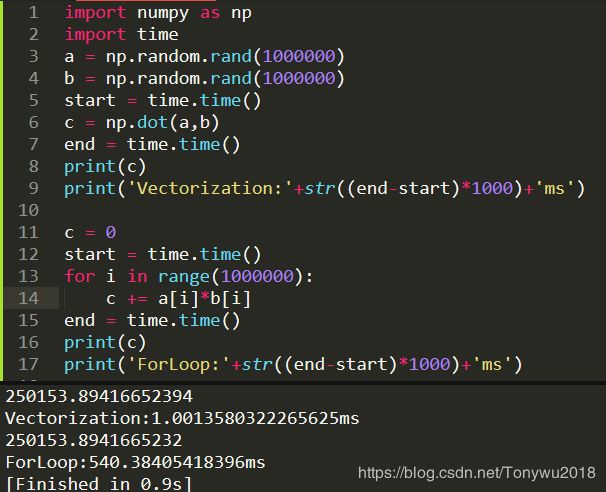
接下来我们比较向量化和![]() 循环在计算速度上的差距:
循环在计算速度上的差距:
可以看到![]() 花费的时间大约是向量化花费时间的
花费的时间大约是向量化花费时间的![]() 倍。
倍。
8. 向量化逻辑回归(Vectorizing Logistic Regression):
python实现向量化的代码:
import numpy as np
Z = np.dot(w.T,X)+b
A = sigmoid(Z)因为![]() ,
, ![]() ,根据
,根据![]() 可得到向量化后的
可得到向量化后的![]() 为:
为:
python代码为:
db = np.sum(dZ)/mpython代码为:
dw = np.dot(X,dZ.T)/m 一次迭代梯度下降算法的代码实现:
import numpy as np
Z = np.dot(w.T,X)+b
A = sigmoid(Z)
dZ = A - Y
dw = np.dot(X,dZ.T)/m
db = np.sum(dZ)/m
w = w - alpha*dw
b = b - alpha*db
9. 逻辑回归代价函数的解释(Explanation of logistic regression cost function):
我们知道预测输出![]() 是Sigmoid函数,其表达式如下:
是Sigmoid函数,其表达式如下:
对上面的式子做变换得到:
我们假设![]() 、
、![]() ,那么上面的式子可以变为:
,那么上面的式子可以变为:
假设数据集中有![]() 个样本,那么得到似然函数:
个样本,那么得到似然函数:
对数似然函数为:
我们要最大化似然函数,即通过![]() 求得参数
求得参数![]() ,等价于通过
,等价于通过![]() 求得参数
求得参数 ![]() ,其中
,其中![]() 为代价函数,其表达是为:
为代价函数,其表达是为: