在多标签学习中,通常我们会假设一个实例的所有标签都已知,但现实情况并不如此。在 AAAI 2018 所接收的论文中,南京大学周志华组提出了从半监督弱标注数据中学习并处理多标签学习问题。该方法假设实例和标签的相似性有助于补充缺失的标签。而且,当标签信息不足时,多个模型的集成通常比单个模型更有效。
传统的监督式学习通常假设每个实例都与一个标签相关联。然而,在现实生活的许多任务中,一个实例通常不止一个标签。传统的基于一个实例对应一个标签的监督学习不能解决这个问题,因此,用来处理与一组标签关联的实例的多标签学习(Zhang and Zhou 2014)受到了很大的关注。
在以前的多标签研究中,训练数据一个基本的假设是我们知道每一个实例的所有相关标签。然而这一点在现实中是不成立的,例如人类可能会给训练图像标注为汽车或道路而忽略行人与建筑。因此标注的不完全性显著地影响多标签学习(Zhou 2017)的性能。
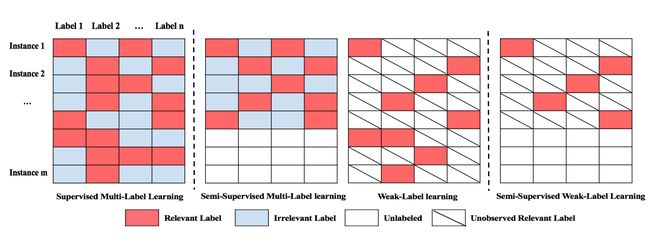
显然,弱标签学习和半监督的多标签学习都不能解决本文所关心的问题。例如,弱标签学习忽略了许多可能非常有用而未标记的实例;半监督多标签学习假定所有相关标签都可用于标记实例,但在我们的情况中并非如此。注意本文中的数据情景学习与以前的多标签学习有很大不同。我们把这种多标签问题称为半监督的弱标签学习。下图举例说明了本论文的学习场景和图 1 中以前的多标签学习框架之间的差异。
图 1:四种多标签学习设定
本论文研究了半监督的弱标签学习问题,提出了 SSWL(半监督弱标签)模型。周志华等研究者的基本假设是,实例和标签的相似性有助于补充缺失的标签。而且,当标签信息不足时,多个模型的集成通常比单个模型更有效。具体来说,他们首先基于平滑假设构造一个正则化项,即类似的实例在其标签集合中应该有相似的概念组合,这要求最终的预测与实例和标签相似性的平滑性同时相关。最后研究者分别为有标签和无标签的实例建立模型,然后我们通过协同正则化框架(Sindhwani, Niyogi, and Belkin 2005)集成多个不同的模型。周志华等研究者将这个问题表示为双凸形式(bi-convex formulation),并提供了一个有效的块坐标下降解决方案。该方法的有效性在实验中得到验证。
论文地址: https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/aaai18ssml.pdf
多标签学习同时处理与多个标签关联的数据对象。以前的研究通常假定每个实例都给出了与每个训练实例相关的所有标签。然而,在许多应用中,例如图像标注,通常很难为每个实例获得完整的标签集合,并且只有部分甚至是空的相关标签集合是可用的。我们把这种问题称为「半监督弱标签学习」问题。在这项工作中,我们提出了 SSWL(Semi-Supervised Weak-Label)模型来解决这个问题。通过考虑实例相似性和标签相似性来补充缺失的标签。利用多个模型的集合来提高标签信息不足时的鲁棒性。我们用高效的块坐标下降算法将目标形式化为双凸优化问题,且实验验证了 SSWL 的有效性。
算法 1 总结了我们提出的伪代码:
更具体来说,我们首先介绍一些符号:
这里 vec(M)是矩阵 M 的向量化,diag(v)是一个以向量 v 为对角元素的对角矩阵,⊗ 是 Kronecker 乘积(张量积)。
用固定的 W bar 和 L 来表示 W
我们可以推导出我们的目标,即找到 W,W bar 和标签相似度矩阵 L,使得下面的目标函数被最小化,
其中 α,β,ζ 是参数。U =(XW)◦C +(XW bar)◦(E - C)是两个模型的综合预测。式(3)一方面考虑实例和标签相似性的平滑性,另一方面,它结合了集成学习的优点以获得稳定的结果。
当 W bar 和 L 固定,我们通过使等式(3)关于 W 的导数为零,得到下面关于 W 的等式,
其中 R =(XW)◦C. 根据定理 1,我们可以将公式 4 重新写为,
这是一个简单普通的线性方程,我们可以使用共轭梯度算法(Møller1993)求解,这是求解线性方程的高效算法。
后面固定 W、L 以更新 W bar 和固定 W、W bar 以更新 L 的具体过程请查阅原论文。
文本分类任务
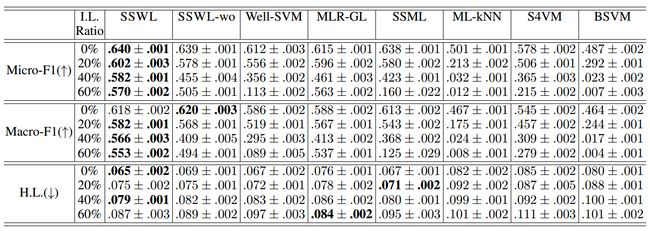
表 2:在 TMC 上的实验结果(平均值±标准差)。↑(↓)表示越大(小)越好。最好的结果标为粗体(成对 t 检验在 95%的显着性水平)。
基因功能分析任务
表 3:酵母的实验结果(平均值±标准差)。↑(↓)表示越大(小)越好。最好的性能或结果标为粗体(成对 t 检验在 95%的显着性水平)。
场景分类任务
表 4:SceneImage 上的实验结果(平均值±标准偏差)。↑(↓)表示越大(小)越好。最好的表现和结果标为粗体(成对 t 检验在 95%的显着性水平)。
图像标注任务
表 5:msrc 上的实验结果(平均值±标准偏差)。↑(↓)表示越大(小)越好。最好的表现和结果标为粗体(成对 t 检验在 95%的显着性水平)。