python 版 排序与搜索
冒泡排序
冒泡排序算法的原理如下:
- 比较相邻的元素。 如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。 在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码:
#coding: utf-8
def bubble_sort(alist):
''' 列表的长度'''
n = len(alist)
for j in range(n-1):
'''j:是从 0 ~ n-2 第一个到倒数第二个'''
for i in range(0,n-1-j):
'''每次比较都减去上次比较的次数'''
if alist[i] > alist[i+1]:
'''前一个数比后一个数大,则交换位置'''
alist[i], alist[i+1] = alist[i+1], alist[i]
if __name__=="__main__":
ls = [12,45,13,65,11,78,56,125,123]
print(ls)
bubble_sort(ls)
print(ls)
选择排序
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最坏时间复杂度 | О(n²) |
| 最优时间复杂度 | О(n²) |
| 平均时间复杂度 | О(n²) |
| 最坏空间复杂度 | О(n) total, O(1) auxiliary |
选择排序的示例动画。红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置。
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对{\displaystyle n}个元素的表进行排序总共进行至多{\displaystyle n-1}次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
代码
#coding: utf-8
def select_sort(alist):
n = len(alist)
"""从0~n-2 到倒数第二个"""
for i in range(n-1):
min_index = i # 最小数的下标赋值
"""从最小数的位置到末尾选出最小的数"""
for j in range(i+1,n):
"""从后面的数中找到比最小数还小,则把位置赋值给 min_index"""
if alist[j] < alist[min_index]:
min_index = j
if min_index != i:
alist[i], alist[min_index] = alist[min_index], alist[i]
if __name__=="__main__":
alist = [12,34,64,23,7,86,37,39]
print(alist)
select_sort(alist)
print(alist)
插入排序
| 使用插入排序为一列数字进行排序的过程 |
|
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最坏时间复杂度 | {\displaystyle O(n^{2})} |
| 最优时间复杂度 | {\displaystyle O(n)} |
| 平均时间复杂度 | {\displaystyle O(n^{2})} |
| 最坏空间复杂度 | 总共{\displaystyle O(n)} ,需要辅助空间{\displaystyle O(1)} |
使用插入排序为一列数字进行排序的过程
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到{\displaystyle O(1)}的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
代码
#coding: utf-8
def insert_sort(alist):
n = len(alist)
#从右边的元素取多少个元素进行这个过程"""
for j in range(1, n):
# j = [1, 2, 3, 4,....n-1]
# i 代表的是内层循环的起始值
i=j
while i > 0: # 从右边的无序序列中取出第一个数,即 i 的位置, 然后将其插入到前面的位置中
if alist[i] < alist[i - 1]: # 后面的一个数比前一个数大 则交换位置
alist[i], alist[i - 1] = alist[i - 1], alist[i]
i -= 1
else:
break
if __name__=="__main__":
alist = [12,34,64,23,7,86,37,39]
print(alist)
shell_sort(alist)
print(alist)
希尔排序
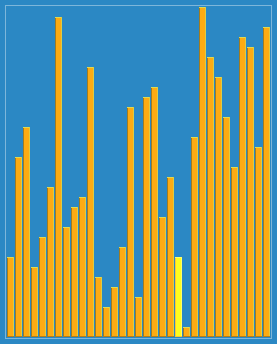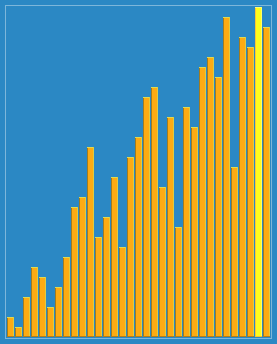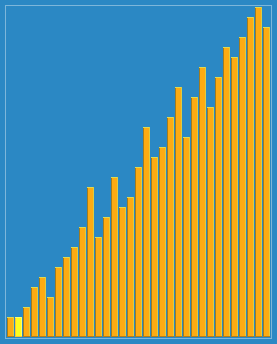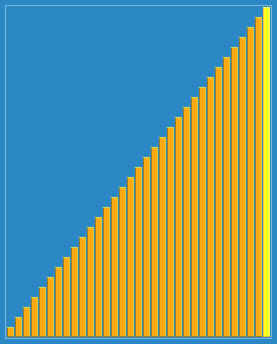 以23, 10, 4, 1的步长序列进行希尔排序。 |
|
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最坏时间复杂度 | 根据步长序列的不同而不同。已知最好的:{\displaystyle O(n\log ^{2}n)} |
| 最优时间复杂度 | O(n) |
| 平均时间复杂度 | 根据步长序列的不同而不同。 |
| 最坏空间复杂度 | O(n) |
希尔排序算法彩条
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
代码
#coding: utf-8
def shell_sort(alist):
n = len(alist)
gap = n //2
# 步长 gap 折半
#从右边的元素取多少个元素进行这个过程"""
while gap > 0: # 循环 gap ~ 1
for j in range(gap, n):
# j = [gap, gap+1, gap+2, .... n-1]
# i 代表的是内层循环的起始值
i=j
while i > 0: # 从右边的无序序列中取出第一个数,即 i 的位置, 然后将其插入到前面的位置中
if alist[i] < alist[i - gap]: # 后面的一个数比前一个数大 则交换位置
alist[i], alist[i - gap] = alist[i - gap ], alist[i]
i -= gap
else:
break
gap //= 2
if __name__=="__main__":
alist = [12,34,64,23,7,86,37,39]
print(alist)
shell_sort(alist)
print(alist)
快速排序
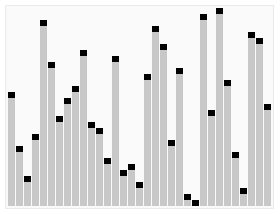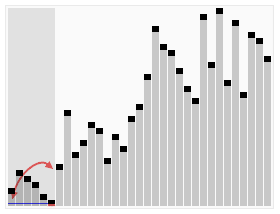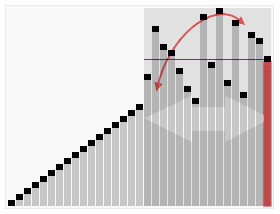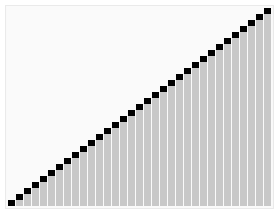 使用快速排序法对一列数字进行排序的过程 |
|
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 不定 |
| 最坏时间复杂度 | {\displaystyle \Theta (n^{2})} |
| 最优时间复杂度 | {\displaystyle \Theta (n\log n)} |
| 平均时间复杂度 | {\displaystyle \Theta (n\log n)} |
| 最坏空间复杂度 | 根据实现的方式不同而不同 |
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),简称快排,一种排序算法,最早由东尼·霍尔提出。在平均状况下,排序{\displaystyle n}个项目要{\displaystyle \ O(n\log n)}(大O符号)次比较。在最坏状况下则需要{\displaystyle O(n^{2})}次比较,但这种状况并不常见。事实上,快速排序{\displaystyle \Theta (n\log n)}通常明显比其他算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地达成。
步骤为:
- 从数列中挑出一个元素,称为“基准”(pivot),
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分割结束之后,该基准就处于数列的中间位置。这个称为分割(partition)操作。
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是零或一,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。