A*算法自学心得

0 关于文章

这篇文章是我从自己的csdn上扣下来的，可能会有些格式错误。
另外，因为本人不会画图不想画图，就从别人那里扣来了一些图，如果有争议，请联系作者：
C20204429

1 概述与引例

A*算法是一个寻径算法
相信同学们都玩过某种游戏LOL人在塔在！！！ ，在你用鼠标点击地面的某个地方的时候，你所操控的人物会十分智能地寻找一条最短的路前进到你所指定的位置，不论范围大小，这种算法都很快。

1.1 类似最短路算法类比

看完这样一个功能，似乎实现起来很简单
似乎我们也可以制作这样一个功能，想一想我们所学过的一些算法:

• floyd算法
  这似乎是一个十分简单的算法，可以解决多源点的问题，利用中转点的思想和一个效率十分低的三重循环，但是由于其效率太低(三重循环，时间复杂度O(n^3))，你其实可以使用这个来制作这样一个功能，也挺方便的是不是啊？把一个大型多人联机实战游戏卡成了PPT，最多也就是玩家把你这个制作者吊起来打一顿“而已”
• dijkstra算法
  这个算法的效率十分不错，使用了一个叫做“松弛”的操作与一个g()数组记录起点到格子的最短距离，时间复杂度O(n^2)，但是如果使用堆优化，可以变成O(n*log(n))，已经完全可以接受了，但是唯一的缺点是不接受负权边。
  其实负权边也可行，只要用玄学修改算法，可以保证正确性但是会被魔学的出题人卡成指数。语出 APOI2013出题人
• SPFA算法
  这个算法据说是bellman-ford算法的改进版感人的是这个算法是一个中国伟大的专家提出的！！！ ，时间复杂度在O(n*m)，这个算法是由一个点进行发散，代码和dijkstra算法很像有一段时间我居然把它和dijkstra算法搞混了 ，它可以支持负权边，但是不支持负环，它没有dijkstra算法太刻板，前者虽不支持负环，但是可以判定并退出，但是后者似乎在负边上就跑不起来

1.2 BFS算法的引入、对比与问题的出现

在1.1中，我们发现似乎三个算法中，dijkstra算法是十分高效的，时间复杂度只有O(n*log(n))
那么我们就从dijkstra算法中开始研究
这里新增一个在没有路障的情况下高效得不能再高效的算法

• BFS算法
  呃？这不是搜索里面的吗？怎么到这里来了？
  这个算法的全名叫做Best-First Search，和BFS(Breadth-First Search)不一样。
  这是一个很贪心的算法，具体的可以看下面的图来对比一下:
• 这是dijkstra算法所找到的正常的 最短路(笔者不会画图，就借了下别人的图):

前文提到，dijkstra算法使用了g()数组来记录从起点到这个格子的距离，在此图中，一目了然的就是“格子越黑，其离起点越近”，而后面的dijkstra算法模拟图也是这个道理。
当然，也可以发现，虽然这个算法找到的最短路，但是搜索区域很大

• 这是BFS算法找到的路(注:我没有叫其最短路，是有原因的，在接下来就可以见到):

这个算法似乎更高效，找到的不仅是“最短路”，而且搜索的区域十分小

注意，这才是最简单的情况，连路径都没有！！

那么，在有路障的情况下，两位参赛选手…呸，两种算法表现又是如何呢？

• dijkstra算法

虽然搜索区域更广了，但是还是找到了最短路

• BFS算法

哦！这时这个算法行不通了，它虽然搜索区域小一些，但是找到的路，连最短路都算不上！

1.3 BFS算法问题的解释与启发式函数

为什么BFS会有这样大的问题呢？一个寻径算法，却找不到最短路，这是个很大的问题！
其实，BFS根本不适用于有路障的图上，注意它的名字Best-First Search，根据我这个英语短填只扣了14分来理解一下它的意思是“最好的最先 搜索”，也就是说它太过于贪心了
再返回看一下BFS算法的两个图：

这两个图中，都有同一个特点，那就是它们都有从黄色到黑色的渐变，格子越黑，其离终点的距离越近。其实，BFS算法的实现，大多数与dijkstra算法是一致的，但是有一点不一样，它使用的函数不叫g()，而是一个叫做启发式函数(heuristic function)的东西，这个玩意儿是干啥的呢？
启发式函数
正如它的名字所说的，它本身的作用其实是一个“启发”的作用，换句话说，它指明了算法搜索的方向，快速地导向了目标节点。
但是凡事有利亦有弊，正如第二个图，它一直按照离终点近的格子走，直到碰到墙壁不是鲁迅先生的碰壁！ 才意识到：哦！我应该换一条路了。但是已经来不及了，所以有时候启发式函数的指向并不是正确的，还有可能找到的路并不是最短的路。这也就是BFS算法出问题的原因。

2 A*算法的诞生

在1.3中，我们已经找到了BFS算法问题的所在，那么，我们最终应该用的是dijkstra算法还是BFS算法？其实不用说也看得出来，其实我们想的是能实现如下状况的算法：

• 在无障碍的情况下：

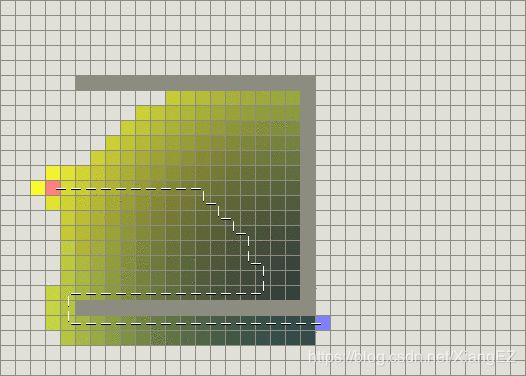
• 在有障碍的情况下

看得出来，上面的两张图中，格子越偏蓝色，其距离目标节点的距离越短。
更明显的是，它似乎综合了dijkstra算法与BFS算法。
这个算法，就是我们这个文章的主角——A*算法

2.1 A*算法的理论深入研究

我们已经知道了，A*算法其实是由dijkstra算法与BFS算法的拆分、组装得来的，那么它应该具有的，应该是两者的优点你总不可能费劲千辛万苦把缺点放在一起吧

• A*对于dijkstra算法的借鉴
  1.1对dijkstra算法的介绍中，似乎提到了一个松弛操作与g()数组，前者大意就是用两个或多个小线段的组合，替代一条大线段原本连接的两个节点，使得这条路径拥有原来的功能，但是权值总和却更小。而后者主要是记录从起点到当前节点的最小花费并利用松弛操作不断更新，这就是A*算法借鉴的部分。
• A*对于BFS算法的借鉴
  BFS算法留给人最深印象的，就是他使用了一个叫做启发式函数的东西，能够快速导向目标。而这也是 A* 算法主要借鉴的部分。
  注意：启发式函数如何使用十分关键，因为它也有弊端，在下文会说明启发式函数对于A*搜索的影响。

2.2.1 A*算法如何利用启发式函数

启发式函数的英文还记得吗？当然记得，是QiFaShiHanShu “heuristic function”，那么这里我们果断一点，就用其首字母“h”来代表启发式函数。

• h(n):从当前格子n到终点的评估距离。
  什么是评估距离？其实就是你用某种出题人喜欢的与题目要求相适应的启发式函数得到的一个从这个点到终点的估计的花费，当然，它可以和现实相出入，但最好不要太大了，不然你就得试着换个距离算法。也就是说，选一个好的启发式函数对于A*算法其实是十分重要的。

2.2.2 A*在网格地图中较常用的启发式函数的算法

• 曼哈顿距离
  这个算法太过简单，不做解释…
  直接上公式了：
  h(n)=d(abs(n.x–goal.x )+abs(n.y–goal.y ))
  其中，d是单位距离的花费（因为在网格图中，每个移动的花费都是一样的，直接乘上去就行了）下文也是一样
• 对角线距离
  在一些可以斜着格子走的图中，曼哈顿距离求到的不一定是最短的路（可以斜着走嘛），这个时候，就可以使用对角线距离了。
  这个也简单，不做解释…
  h(n)=max(abs(n.x-goal.x),abs(n.y-goal.y))d
• 欧几里得距离
  有一些奇奇怪怪的出题人，如果他们想的是移动方向不局限于横着、竖着、斜着，而是360度无死角地移动，那应该怎么办？很简单，把出题人吊起来群殴一顿再威胁他改题你可能更需要的是直线距离。
  这个也很简单，不做解释…
  h(n)=sqrt((n.x-goal.x)^2 + (n.y-goal.y)^2)d
  有时候可以把它平方一下，但是这样做似乎是找死…
  为什么呢？后面就知道了来打我啊

2.2 A*算法总体功能

综合前面的2.1，我们现在可以把A*算法的功能列举出来了：

• 有一个g()数组
  这个g()数组应该和dijkstra算法的g()数组具有同样的功能，都是记录从起点到当前格子的最短距离。
• 松弛操作
  这个操作也是来源于dijkstra算法，可以倒回去看，这个不再多说。
• 启发式函数h()
  这个操作来源于BFS算法，利用某种适合题目的距离算法，快速导向目标节点。

2.2.1 具体功能剖析之双数组综合

这个题目是不是很拽？
通过2.2我们发现，似乎这个有两个数组，分别是g()与h()，那么我们应该用哪一个呢？
似乎我们可以分类讨论…

• 只用g()数组
  如果只用g()数组，似乎这个看上去很高档的A*算法就变成了dijkstra算法（dijkstra算法也是只有一个g()数组，而这些最短路算法实现都差不多，所以很相似，或者一模一样）
• 只用h()数组
  同样的，如果我们只用h()数组，A*算法就退化为了BFS算法。

难道就只能在二者中择其一？不，这里还有一种情况！

• 不要g()数组和h()数组，我们来快乐暴瘦吧！ 综合g()数组与h()数组
  那么我们怎么综合呢？想到的一定是平均数对吧！但是我们想一下，每个格子都取 (g(i)+h(i))/2 中这个2似乎有些麻烦了，把每个数的 (g(i)+h(i))/2 都乘2，那么这个“/2”就不在了，于是我们就得到了一个东西：
  f(i)=g(i)+h(i)
  为什么要在前面加一个f(i)?因为我太懒了，懒得写…
  这个f()数组，我们就可以把它当成一个评估值，通过这个值来进行搜索。
  其实我们也可以感受到，这个f()函数的值，对于A*的正常搜索很重要。
  我们可以按照这个来执行搜索，效果要好很多！

2.2.2 综合数组f()的细节处理

• 单位统一
  相信各位同学们都有同样的经历：在你们小学或者初中的时候，是否曾因为单位问题WA？
  其实，在使用数组f()时有同样的问题，单位！
  因为f()并不只是一个数组，它代表了两个数组，h()与g()，而这两个数组如果单位不统一，造成的结果就是其中一个数组很大，另一个数组很小！
  打个比方，比如你的g()数组使用的是以 米（m） 为单位，而h()数组以 千米（km） 为单位，那么f()数组就会认为，g()数组中的值过大，h()数组的值过小，换句话说，f()数组的取值就会直接由g()数组的值影响，反而h()数组没有什么用，那么这个算法就退化为了dijkstra算法（若h()数组过大，则退化为BFS算法）
• 启发式函数的精确性
  如果你的启发式函数精确地等于或者相似于实际最佳路径，那么A* 因为有一个十分精确的导向而扩展的结点就会非常少。而A* 算法内部发生的事情是：在每一结点它都计算f(n) = g(n) + h(n)。当h(n)和它应该对应的g(n)匹配时，f(n)的值在沿着该路径时将不会改变。不在最短路径上的所有结点的f值均大于最短路径上的f值。而若是已经有较低f值的结点，A*将不考虑f值较高的结点，因此它肯定不会偏离最短路径。也就是说，一个精确的启发式函数，是能够起到很好的剪枝作用！

2.3 A*算法的代码（伪）

我不说话，上来就抛一张从别人那里扣来的伪代码：

具体的代码实现，大家应该可以了吧！

————————————————————————————

制作人：C20204429你以为我会给你透露姓名吗？不可能！

再说一遍，多年准备一场空，不打long long见祖宗！

本人亲测！

参考文献网址：
http://theory.stanford.edu/~amitp/GameProgramming/

如果对A*算法过程不清楚，推荐以下博客：
https://blog.csdn.net/zhulichen/article/details/78786493