使用森林优化算法的特征选择

转自:FeatureselectionusingForestOptimizationAlgorithm
Manizheh Ghaemi a,n, Mohammad-RezaFeizi-Derakhshi b

摘要:特征选择作为组合优化问题是数据挖掘中的重要预处理步骤，借助于去除不相关冗余特征，可以提高学习算法的性能。由于进化算法被报告适用于优化任务，所以森林优化算法（FOA） - 最初被提出用于连续搜索问题 - 适用于作为离散搜索空间问题的特征选择。因此，本文提出使用森林优化算法（FSFOA）的特征选择，以从数据集中选择更多的信息特征。拟议的FSFOA在几个现实世界的数据集上得到验证，并与HGAFS，PSO和SVM-FuzCoc等其他方法进行比较。实验结果表明，FSFOA可以提高分类器的分类精度
选定的数据集。此外，我们比较了FSFOA的维数降低与其他可用的方法。

1.介绍
  知识发现的必然步骤之一就是数据挖掘和数据挖掘得到的知识在许多趋势中被使用;像商业和医疗用途[6,15,20,37]。这些天，数据库中收集和存储的功能数量有所增加，但并不是所有的功能对数据挖掘都是有用的，所以一些功能是完全无关或冗余的[8,10,36,23]。这些特征不仅在知识发现的过程中没有用，而且增加了结果的复杂性和不可理解性。因此，特征选择有助于降低数据集的维度在数据挖掘之前。在具有许多特征的大数据库中，当存在n个特征时，评估所有特征子集的时间复杂度是指数（O（2n））[31]，这是不可能的。因此，特征选择方法是数据挖掘的基础，为后期学习任务保留有用的特征，同时忽略最不相关和不太重要的[11]。事实上，特征选择技术忽略了不相关的特征所以学习过程可以更有效地完成。也证明了特征选择能够提高机器学习算法的分类精度，如KNN分类器[11]。

  特征选择是特征权重问题的特殊情况[34]。 许多研究表明特征权重的有益效果[1,9,27,30,32,33]。 在特征加权问题中，特征被赋予一个值，该值表示其在机器学习过程中的重要性，但是在特征选择问题中，特征被保留或删除，并且权重被限制为只有'0'和'1'。 事实上，特征选择算法是使用二进制权重的特征加权算法的适当子集
（即0或1）。

  已经证明，特征选择对分类器的精度和复杂度有影响[11]。 用于评估所选特征子集的主要使用标准是新实例（testdataset）上的分类精度（CA）。 实际上，我们期望在特征选择的帮助下进行维数降低会提高分类精度，或至少保持不变。

  本文的目的是利用FOA作为新的进化算法，选择数据集的有用特征。 由于FOA被报道适用于连续搜索空间，本文尝试研究FOA在特征选择（FS）中作为离散搜索问题的性能，并且引入了一种名为特征选择的方法，该方法使用森林优化算法（FSFOA）。 实际上，FSFOA搜索最佳特征子集，目的是提高一些分类器的分类精度，作为包括KNN，C4.5和SVM分类器在内的学习算法。 本文的贡献有两个方面：适应FOA解决离散问题，并借助离散FOA来解决特征选择问题，导致了FSFOA方法。

  本文的其余部分组织如下。第2节介绍了特征选择方法的概述。 森林优化算法（FOA）的概述在第3节中给出。在第4节中，介绍了FOA用于特征选择（FSFOA）的应用，第5节介绍了FSFOA的实验和结果。最后，第6节 总结主要结论。

2.特征选择方法概述
  目前，许多研究人员已经解决了特征选择（FS）问题，还需要更多的尝试来进一步加快在数据挖掘数据库中选择信息和实用功能的过程。

  基于机器学习算法的FS文献中最早的方法是滤波器[11,12]。在所有的滤波器中，使用基于诸如信息增益和距离之类的数据的一般特征的启发式技术来代替学习算法。特征选择中的另一种方法是包装方法[11,19]。与过滤器相反，包装器使用学习算法来研究所选特征的价值[41]。一般来说，包装器比过滤器产生更好的效果;因为在使用包装方法时，考虑学习算法和训练数据之间的关系。包装纸的众所周知的缺点是它们比过滤器慢;因为必须为每个选定的要素子集重复执行学习算法。有时使用过滤器包装方法的混合。混合方法将学习算法中的特征选择进行集成，以利用包装器和滤波器的优点[11]。忽略过滤器或包装方法的特征选择方法，它们可以匹配以下任何组：完全搜索，启发式搜索和元启发式方法。
  Almuallim和Dietterich提出了FOCUS方法，它完全搜索搜索空间，达到将训练数据分成纯类的最小特征集[2,3]。但是通过n个特征处理，有（2^n）-1个可能的特征子集，所以评估所有的子集在具有许多特征的数据集中几乎是不可能的。结果，在具有许多特征的大型数据集中，完全的搜索方法很少用于特征选择。
  特征选择问题的启发式方法包括贪婪爬坡算法[25,26]，分支绑定法，波束搜索和最佳第一算法。贪婪爬坡算法评估所有局部变化以选择相关特征[11,25]。 SFS（顺序前向选择）和SBS（顺序向后选择）是两种爬坡方式。 SFS从一组空白的特征开始，算法的每个步骤将一个信息特征添加到选定的集合中;但是，SBS启动将完整的功能集合，并且在每个步骤中，省略了冗余或不相关的特征之一。双向搜索是同时考虑添加和删除特征的另一种方法[11]。 SFS和SBS算法的主要缺点是“嵌套效应”问题;这意味着，当变更被认为是积极的（添加或删除功能）时，没有机会重新评估该功能。为了克服SFS和SBS算法的“嵌套效应”，引入了SFFS（顺序前向浮动选择）和SBFS（顺序前向浮动选择）[24]。最好的第一搜索是另一种喜欢爬山的方法，它考虑到搜索空间的局部变化，但是与爬山方法不同，它可以在搜索空间中进行追溯[11]。
  启发式算法在比较时间复杂度方面表现优于完整的搜索方法，但最近，诸如遗传算法（GA），粒子群智能优化（PSO）和蚁群优化（ACO）等元启发式算法显示出更理想的结果。元启发式方法的主要优点是它们可接受的时间复杂度。由于元启发式搜索方法的随机性，遗传算法，粒子群优化算法和蚁群优化在特征选择领域的应用已经取得了有希望的成果[18]。

  其中一些总结如下。
  Hamdani等人提出了一种基于具有双编码染色体表示和新评估函数的分层遗传算法的新算法[13]。为了最小化计算成本并加快了收敛速度，他们使用了具有均匀和异构人口的分层算法。 Zhu等人提出了一种新的算法，它是遗传算法和局部搜索方法的组合[40]。首先，随机生成GA群体，然后将本地搜索应用于群体中的所有个体，以提高分类准确性并加快搜索过程。 Tan et al。在GA中使用基于包装方法[31]的SVM（支持向量机）。在他们提出的算法中，GA搜索最佳特征子集，SVM的分类精度指导搜索过程。 Gheyas等人将模拟退火（SA）和GA组合使用SA和GA的优点[10]。在他们提出的SAGA中，GA通过交叉算子有助于逃离SA的局部最优。 Nemati等人提出了GA和ACO的新混合算法，以利用这两种算法的优点[22]。在其算法中，ACO执行本地搜索，而GA用于执行全局搜索。 Sivagaminathan等使用ACO搜索近最优

3.森林优化算法（FOA）概述
  森林优化算法是一种进化算法，其灵感来自森林中几棵树的过程[9]。 提出了FOA来解决连续的搜索空间问题，但在本文中，我们尝试将其调整为用于离散搜索空间问题，如特征选择。 

  FOA涉及三个主要阶段：

  1 - 树木的本地播种，

  2 - 人口限制和

  3 - 全球种植树木。 

  图1显示了FOA的流程图。 FOA开始于该算法中形成森林的初始种群（解决方案）。 每个树代表了问题的潜在解决方案。 除了变量的值之外，树还有一部分表示相关树的“Age”。 每个新生成的树的“Age”设置为“0”[9]。

  在树木种植程序开始的时候，一些种子落在父树下面，然后变成幼树[9]。这是通过当地种子在FOA中模拟的。初始化树木后，当地播种阶段将对“年龄”0的树进行模拟，以模拟附近的树木种子。那么所有的树，除了新生成的树，变老，他们的“年龄”增加了'1'。该阶段模拟算法的本地搜索。
  下一阶段是人口限制，其中“年龄”大于“生命时间”参数的树木将从森林中省略，并形成候选人群[9]。另外在人口限制阶段，森林的其余树木根据其适应值进行分类，如果森林的整棵树数量超过预定义的“区域限制”参数，额外的树木将加入候选人人口也是。在全球播种阶段，选择候选人口的百分比。来自候选人口的选定树将被用于全球播种阶段。全球播种阶段模拟FOA的全局搜索[9]。 FOA的下一个阶段是根据其适合度值更新选择最佳解决方案的最佳树，并将其“Age”设置为0，以避免老化，然后从森林中删除最佳树。这些阶段将继续迭代，直到满足终止标准。森林优化算法有5个参数，应在算法开始时进行初始化[9]：
 1。“本地播种变化”或“LSC”，
 2。森林或“地区限制”的局限性，
 3。树的最大允许“年龄”，被称为“生命时间”参数，
 4。在全球播种阶段候选人口的百分比或“转移率”，
 5。在全球种子阶段，其值将被改变的变量的数量是该算法的另一个参数，并被命名为“全球播种变更”或“GSC”。
  由于FOA被提出用于连续空间问题，在本文中，我们将FOA适用于离散空间问题，如特征选择。特征选择的森林优化算法的伪代码被称为FSFOA，如算法1所示。如算法1所示，FOA中需要适应特征选择问题的变化应在初始化，局部播种和全局播种阶段在下一节中，更详细地说明了处理特征选择问题的离散搜索空间的FSFOA阶段。

Algorithm 1

FSFOA (life time, LSC, GSC, transfer rate, area limit)
Input: life time, LSC, GSC, transfer rate, area limit
Output: The best feature set with the highest fitness
1: Procedure FSFOA
2: Initialize forest with random 0/1 trees
3: Each tree is a (D+1)-dimensional vector x (D is the number of all features).
4: The “Age” of each tree is initially zero.
While stop condition is not satisfied do
1: Perform local seeding on trees with Age 0
2: Fori=1: “LSC” do
3: Randomly choose a variable of the selected tree
4: change from 0 to 1 or vice versa
5: end for
6: Increase the Age of all trees by 1
7: Population limiting
8: Global seeding
9: Choose “transfer rate” percent of the candidate population
10: for each selected tree do
11: Choose “GSC” variables of the selected tree randomly
12: change from 0 to 1 or vice versa
13: end for
14: Update the best so far tree
15: Sort trees according to their fitness value
16: Set the Age of the best tree to 0
End While
5: end procedure
Return the best tree which shows the best selected feature subset

4.采用森林优化算法（FSFOA）提出的特征选择功能选择问题的FOA阶段如下。

4.1。初始化树
  森林被随机生成的树初始化[9]。首先，FSFOA中的每个树的每个变量随机地用'0'或'1'初始化。如果数据集有n个特征，每个树的大小将为1 *（n + 1）;其中一个变量显示该树的“年龄”。树中的每个“1”表示相应的特征被选择，因此涉及机器学习过程，并且每个“0”表示在学习过程中排除相关特征。首先，每棵树的“年龄”被认为是“0”，但是在每次迭代中的本地播种将增加除本地播种阶段中新生成的树之外的所有树的“年龄”。
4.2。当地播种
  这个阶段将每棵树的一些邻居用“Age”0添加到森林[9]。为了在FSFOA中模拟这个阶段，对于“Age”0的森林的每个树，随机选择一些变量（“LSC”参数决定所选变量的数量）。然后所选变量的值从0改变为1，反之亦然。此过程模拟搜索空间中的本地搜索;因为每次通过在学习算法之前添加和删除该特征来评估一个特征的重要性。图2示出了一棵树上的本地播种运算符的示例，其中数据集的特征数为5，“LSC”的值被认为是2.在执行本地播种阶段之后，“Age”除新生成的树之外的所有树都增加了1。

4.3。人口限制
  在这个阶段，森林中将省略两系列树木，形成候选人群：1 - “年龄”大于“生命时间”参数的树木，2 - 分类树后超过“面积限制”参数的额外树木根据他们的健身价值。这个阶段形成候选人口，候选人群的预定百分比在后来在全球播种阶段使用。
4.4。全球播种
  为了在FSFOA中执行这一阶段，首先从候选人群中选出一棵树，随机选择一些变量。所选变量的数量由“GSC”参数确定。然后，每个选定变量的值将被否定（从0变为1，反之亦然）。但是这次添加或删除某些功能是同时考虑的，而不仅仅是一个功能。该运算符在搜索空间中执行全局搜索。在一棵树上执行此操作符的示例如图3所示。在图3中，“GSC”参数的值被认为是3（3个变量被否定以形成新树）。

4.5。更新最好的树
  在这个阶段，根据其适应度值对树木进行分类后，选择具有最高适应度值的树作为最佳树，其“年龄”设置为“0”。这些阶段被迭代地执行，直到满足停止条件。
4.6。健身功能
  K最近邻（KNN）是许多懒惰学习算法的基础[33]，但它具有很高的存储要求和噪声敏感性等缺点。所以很多研究人员试图解决这些缺陷。特征选择（FS），原型生成/选择和特征加权（FW）方法都用于进一步提高KNN的性能[9,33]。借助于使用FOA的特征选择，我们尝试提高了一些分类器的性能，包括KNN（K∈{1,3,5}）。换句话说，一些分类器的分类精度被用作我们的实验中的适应度函数。在此需要选择K最近邻（1-NN，3-NN和5-NN），支持向量机（SVM）和C4.5（J48）分类器。有关分类器配置的更多说明，请参见第5.3节。
  因为对训练和测试数据集分配不同百分比的数据集可能会影响结果[42]，特别是在具有少量实例的数据集中，所以在我们的实验中，数据集根据不同的方法进行分区。这些方法包括10倍交叉验证方法; 70％的培训和30％的测试数据集，还有2倍交叉验证。根据这些方法报告5.3节中的实验结果，需要比较。报告训练数据集的结果对于所选特征的性能来说不是很好的指标，因为过度拟合问题的可能性很大;报告测试准确性也是如此。过度拟合问题的一个很好的解决方案是将数据集分为3组：训练，验证和测试数据集。因此，验证集将用于防止过拟合问题。但是这种方法在具有少量样本的数据集中可能是有问题的;因为数据集的某种程度将被忽略，并被用作验证集。由于本文中选择的小数据集，在放弃测试数据集之后，我们没有放弃验证集，而是使用10次交叉验证本身训练数据集;训练集分为10组，10部分9部分作为训练集，其余部分用于验证需要，该过程重复10次，最后报告10次平均运动。
  之后，训练阶段已经完成，除了训练数据集之外，使用看不见的测试数据集是不可避免的，最后所有候选特征子集都在相同的测试数据集上进行评估。换句话说，由于测试数据集的最后10次运行的平均结果被报告为最终结果。在第5部分的实验中报告了不可见测试数据集上的实验的分类精度（CA）和尺寸减小（DR）。分类精度是特征选择验证的有效方法[38]，其定义为等式（1）;其中N_CC是正确分类的数量，N_AS表示数据集的所有样本的数量。尺寸减小比如公式（2），其中N_SF是所选特征的数量，N_AF是每个数据集的所有特征的数量[5]。
（1）CA = N_CC / N_AS
（2）DR = 1-（N_SF / N_AF）


  赵等人使用适应度函数，它是分类精度，所选特征的数量和特征成本的组合[39]。选择信息特征的另一个目标函数考虑了特征的内部关系[23]，其测量特征的类内和类间相关性。此外，可以在这种需要中使用目标函数的组合。在本文中，我们将分类精度视为我们的适应度函数，但是我们还将我们提出的FSFOA方法的维数降低与其他方法进行了比较。同样，当比较结果时，我们已经使用了相同的分区和与其他方法相同的分类器，这些将在下面提到。

5.实验和结果
  提出的FSFOA使用11个数据集进行验证。从UCI机器学习库[4]获得十个数据集，并从微阵列数据集中获得高数据集（“SRBCT”）。在我们的实验中，我们使用了公开可用的包WEKA，它是一个基于Java的机器学习工具包。 WEKA软件的KNN，SVM和J48分类器在我们的实验中被使用。所有的实验都是在具有Intel Core i3 CPU（2.40 GHz）和4 GB RAM的华硕机器上进行的，主要的编程语言是Java。
5.1。数据集
  所选择的基准数据集包括“电离层”，“玻璃”，“分割”，“肝炎”，“SRBCT”，“心脏病”，“克利夫兰”，“车”，“皮肤病学”数据集。这些数据集涵盖了小，中，大尺寸数据集的例子。所选数据集的总结如表1所示。表1包含特征数（#features），类数（#class）和每个数据集的实例数（#instances）。在特征选择问题中，如果特征数分别属于[0,19]，[20,49]或[50，∞]，则数据集小规模，中等规模或大规模数据集[30]。因此，11个数据集中的6个数据集是小规模数据集，其中3个是中等规模数据集，“Sonar”和“SRBCT”数据集是大规模数据集。

Table 1

Dataset	#Features	#Instances	#Class
Heart-statlog	13	270	2
Vehicle	18	846	4
Cleveland	13	303	5
Dermatology	34	366	6
Ionosphere	34	351	2
Sonar	60	208	2
Glass	9	214	7
Wine	13	178	3
Segmentation	19	2310	7
SRBCT	2308	63	4
Hepatitis	19	155	2

5.2。 FSFOA参数用于我们的实验
  FSFOA的参数定义如下。 参数中，“寿命时间”参数，“区域限制”和“传输速率”的值不依赖于数据集的大小[9]。 所以我们将考虑以下这些参数值：“寿命时间”= 15，“面积限制”= 50，“传输率”= 5％。 因为“LSC”和“GSC”参数的值取决于每个数据集的特征数，所以这些参数的值分别如表2所示。根据[9]中的实验，我们将设置值 的“LSC”参数为每个数据集维数的1/5。

Table 2

Dataset	#Features	“LSC”	“GSC”
Heart-statlog	13	3	6
Vehicle	18	4	9
Cleveland	13	3	6
Dermatology	34	7	15
Ionosphere	34	7	15
Sonar	60	12	30
Glass	9	2	4
Wine	13	3	6
Segmentation	19	4	9
SRBCT	2308	460	700
Hepatitis	19	4	10

5.3。结果和比较
  我们比较了我们提出的FSFOA方法与其他一些方法。我们实验的所有结果以95％置信区间报告。选择用于比较的特征选择算法是Hu等人提出的邻域软边缘（NSM）方法。 [14]，Moustakidis等人的SVM-FuzCoc [21] Huang [16]，FS-NEIR的FS（HGAFS）混合遗传算法，采用Zhu等人的不同特征评估标准。 [40]，Tabakhi等人提出的一种基于蚁群优化（UFSACO）的无监督特征选择算法。 [29]和PSO（4-2），它是Xue等人基于PSO的方法。 [35]。
  其中HGAFS使用支持向量机。 SFS，SBS和SFFS是贪婪的方法之一，从[21]的文章中选择。 SVM-FuzCoc，PSO（4-2）和NSM分别使用1NN，5NN和3NN分类器。 UFSACO和FS-NEIR报告了J48分类器的分类精度。这些方法的总结如表3所示。另外，表3显示了每种方法使用数据集的方式（10次交叉验证，70％培训和30％测试，或2次交叉验证进行培训和测试） 。

Table 3

Method name	Dataset splitting	Description/year
SFS, SBS, SFFS	70–30	Greedy hill climbing methodsa[21] (2010)
NSM	10-fold	Neighbor soft margin [14]/2010
SVM-FuzCoc	70–30%	A novel SVM- based FS [21]/2010
HGAFS	2-fold	Hybrid genetic algorithm for FS [16]/2007
FS-NEIR	10-fold	Neighborhood effective information ratio based FS [40]/2013
UFSACO	70–30	Unsupervised FS algorithm based on ACO [29]/2014
PSO(4-2)	10-fold	Particle swarm optimization for feature selection [35]/2013

  FSFOA的分类精度和维数降低以及表3的其他方法报告在图4的表中。图4中FSFOA报告的结果超过10次独立运行。对于每个数据集，最好的分类精度和最佳尺寸降低（DR）以粗体突出显示。图4中的尺寸减小（DR）由公式（2）。为了提供公平的比较，对于每个数据集，报告根据不同百分比的数据集分裂的多个结果，并且在我们的比较中考虑它们。此外，对于每个方法，在每个表中呈现所使用的分类器，即KNN，SVM或J48。分类器的配置参数摘要如表4所示。这表明KNN分类器在不同的K值下使用比较需要的K（K∈{1,3,5}），并且将Weka的J48分类器用作基于决策树的方法。 SVM分类器的核函数是径向基函数（Rbf-svm）。

Fig. 4 . Comparison between the Classification Accuracy (Accuracy) and Dimension Reduction (DR) obtained by FSFOA and other available methods on “Heart-statlog”, “Cleveland”, “Vehicle”, “Dermatology”, “Sonar” “Ionosphere”, “Glass”, “Segmentation”, “Hepatitis”, “SRBCT” and “Wine” datasets.

Table 4

Classifier	Configuration
KNN	K=1, K=3, K=5
C4.5	J48
SVM	rbf kernel

  从图4的表可以看出，与所有选择的方法相比，“心脏统计”，“电离层”和“分割”数据集的分类精度（CA）有所改善。在所选择的方法中，有GA_based和ACO_based方法。这表明FOA可以通过减少这些数据集中的冗余特性来提高KNN，J48和SVM分类器的性能。在数据集“声纳”，“酒”，“肝炎”，“克利夫兰”，“皮肤病学”和“玻璃”中，FSFOA几乎可以在所有选定的比较方法中胜出; FSFOA在这些数据集中排名第二，而且表现不佳。在“车辆”数据集中，FSFOA可以胜过仅具有相同分区和分类器的方法之一。 FSFOA在“SRBCT”数据集中没有表现出色。 “SRBCT”数据集是唯一的数据集，其特征数量远大于样本数量;这使得难以选择适当的预测特征。由于样本数量不足以选择更多的信息特征，并且应用传统方法会导致差的结果。此外，该数据集被划分为70％-30％的培训和测试数据集;这使问题更糟;因为数据集的某些扩展在训练阶段被忽略。这表明在具有许多特征的大型数据集中的特征选择以及样本数量有限是一个具有挑战性的问题，值得更多的研究。
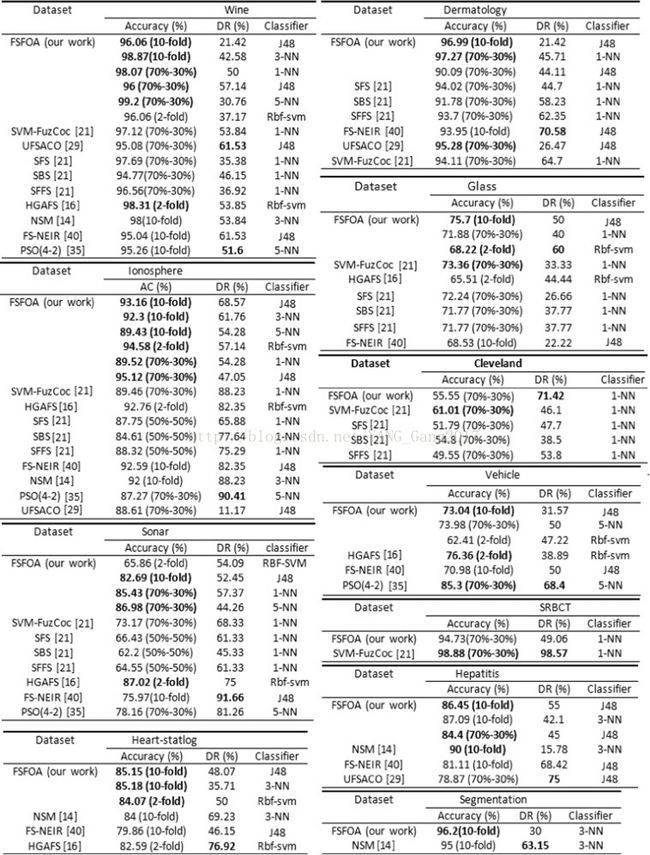
  比较图4中方法的DR，显然FSFOA不能超过选定的方法;因为如前所述，所选特征的数量不涉及每个潜在解的适应度评估，分类精度被认为是适应度函数。为了获得更好的性能说明，我们在图5的图表中显示了结果。对于数据集“肝炎”和“车辆”，根据J48分类器对两种选择的方法进行比较，数据集“皮肤病学”，“声纳”，“在图5的图形比较中选择了SRBCT“，”Wine“，”Heart-statlog“，”Ionosphere“，”Glass“，”Cleveland“和”Segmentation“KNN分类器。

  在比较图4的结果和图5的图表时，根据分类精度，FSFOA在11个数据集（“心脏统计”，“电离层”和“分割”）中的其他方法性能要好于其他方法。在数据集“皮肤病学”，“声纳”，“葡萄酒”，“玻璃”，“克利夫兰”和“肝炎”中，FSFOA胜过其他许多方法，除了具有第二等级的一种方法外。在其他两个数据集中，FSFOA不能具有理想的性能。在所选择的比较方法中，有使用GA，PSO和ACO的方法;这是众所周知的算法。这些结果表明，FSFOA在解决特征选择方面具有可接受的性能，成为一个真正的优化问题。

结论
  特征选择被认为是机器学习和模式识别中重要的预处理步骤。已经提出了许多启发式和元启发式方法来解决这个问题。
  在本文中，我们尝试使用森林优化算法（FOA）来解决特征选择问题。据报道，FOA适用于连续搜索空间问题，因此我们调整了特征选择问题的离散搜索空间的FOA阶段，并提出了FSFOA算法。
  为了调查FSFOA的性能，我们从UCI仓库中选出了一些知名的数据集，并将FSFOA的结果与其他方法进行了比较。在所选择的比较方法中，有GA，ACO和PSO算法。实验结果表明我们的方法在大多数选定数据集中的优越性。在本文中，我们使用了WEKA软件的KNN，SVM和J48分类器来评估每种潜在解决方案的适应度，并将分类精度视为我们的适应度函数。
  本研究表明，FOA是功能选择问题的有效搜索技术，但进一步的研究也受到欢迎。对于我们未来的研究，我们将尝试调查FSFOA在具有大量功能的超大数据集中的性能（例如超过10,000）;因为数据集的大小在功能和实例的数量上都增加了这些日子，而在非常大的数据集中的数据挖掘是一个很大的问题。另外，为了提高维度降低率（DR），涉及适应度功能中所选特征的数量将是我们的特征尝试。这可以通过多目标适应度功能来实现，该功能同时考虑了分类精度和所选功能的数量。

References

[1]

W. Aha David, Feature weithing for lazy learning algorithms, in: Huan Liu, Hiroshi, Motoda (Eds.), Feature Extraction Construction and Selection: a Data Mining Perspective, Kluwer Academic Publishers, Massachussetts, 1998, 13–32.

[2]

Almuallim Hussein, Thomas G. Dietterich Learning Boolean concepts in the presence of many irrelevant features

Artif. Intell., 69 (1) (1994), pp. 279-305

[3]

H. Almuallim, T.G. Dietterich, Learning with many irrelevant features, in: Proceedings of the AAAI, vol. 91, 1991 July 14, 547–552.

[4]

C. Blake, E. Keogh, C.J. Merz, UCI Repository of machine learning databases, University of California, Irvine, 〈http://www.ics.uci.edu/~mlearn/MLRepository.html〉.

[5]

M. Jose Cadenas, M. Carmen Carrido, Raquel Martinez Feature subset selection filter-wrapper based on low quality data

Expert Syst. Appl., 40 (2013), pp. 6241-6252

[6]

K.J. Cios, G. William Moore Uniqueness of medical data mining

Artif. Intell. Med., 26 (1) (2002), pp. 1-24

ArticlePDF (326KB)

[7]

M.E. ElAlami A filter model for feature subset selection based on genetic algorithm

Knowl.-Based Syst., 22 (5) (2009), pp. 356-362

ArticlePDF (283KB)

[8]

E. Gasca, J.S. Sanchez, R. Alonso Eliminating redundancy and irrelevance using a new MLP-based feature selection method

Pattern Recognit., 39 (2006), pp. 313-315

ArticlePDF (153KB)

[9]

Manizheh Ghaemi, Mohammad-Reza Feizi-Derakhshi Forest optimization algorithm

Expert Syst. Appl., 41 (15) (2014), pp. 6676-6687

ArticlePDF (2MB)

[10]

A. Gheyas Iffat, S. Smith Leslie Feature subset selection in large dimensionality domains

Pattern Recognit., 43 (2010), pp. 5-13

[11]

A. Hall Mark, Correlation-based feature selection for machine learning (Ph.D. thesis), Hamilton, NewZealand, 1999.

[12]

A. Hall Mark, Correlation-based feature selection for discrete and numeric class machine learning, in: Proceedings of 17th International Conference on Machine Learning, 2000, 359–366.

[13]

M. Hamdani Tarek, Jin-Myung Won, M. Alimi Adel, Karray Fakhri Hierarchical genetic algorithm with new evaluation function and bi-coded representation for the selection of features considering their confidence rate

Appl. Soft Comput., 11 (2011), pp. 2501-2509

[14]

Q. Hu, X. Che, L. Zhang, D. Yu Feature evaluation and selection based on neighborhood soft margin

Neurocomputing, 73 (10) (2010), pp. 2114-2124

ArticlePDF (1MB)

[15]

Q.H. Hu, D. Yu, J.F. Liu, C. Wu Neighborhood rough set based heterogeneous feature subset selection

Inf. Sci., 178 (2008), pp. 3577-3594

ArticlePDF (344KB)

[16]

J. Huang, Y. Cai, X. Xu A hybrid genetic algorithm for feature selection wrapper based on mutual information

Pattern Recognit. Lett., 28 (2007), pp. 1825-1844

ArticlePDF (356KB)

[17]

Md. Kabir Monirul, Md. Shahjahan, Kazuyuki Murase A new local search based hybrid genetic algorithm for feature selection

Neurocomputing, 74 (2011), pp. 2914-2928

[18]

Md. Kabir Monirul, Md. Shahjahan, Kazuyuki Murase A new hybrid ant colony optimization algorithm for feature selection

Expert Syst. Appl., 39 (2012), pp. 3747-3763

[19]

Ron Kohavi, H. John George Wrappers for feature subset selection

Artif. Intell., 97 (12) (1997), pp. 273-324

ArticlePDF (4MB)

[20]

N. Lavrac Selected techniques for data mining in medicine

Artif. Intell. Med., 16 (1) (1999), pp. 3-23

ArticlePDF (289KB)

[21]

S.P. Moustakidis, J.B. Theocharis SVM-FuzCoC: a novel SVM based feature selection method using a fuzzy complementary criterion

Pattern Recognit., 43 (2010), pp. 3712-3729

ArticlePDF (1MB)

[22]

Shahla Nemati, Mohammad Ehsan Basiri, Nasser Ghasem Aghaee, Mehdi Hosseinzadeh Aghdam A novel ACO-GA hybrid algorithm for feature selection in protein function prediction

Expert Syst. Appl., 36 (2009), pp. 12086-12094

ArticlePDF (424KB)

[23]

G.A. Papakostas, A.S. Polydoros, D.E. Koulouriotis, V.D. Tourassis Evolutionary Feature Subset Selection for Pattern Recognition Applications

INTECH Open Access Publisher (2011)

[24]

P. Pudil, J. Novovicov, J. Kittler Floating search methods in feature selection

Pattern Recognit. Lett., 15 (1994), pp. 1119-1125

ArticlePDF (505KB)

[25]

Bart Selman, Carla P. Gomes Hill‐climbing Search, Encyclopedia of Cognitive Science

(2006)

[26]

B. Selman, H.J. Levesque, D.G. Mitchell, A new method for solving hard satisfiability problems, in: Proceedings of the AAAI, vol. 92, July 12, 1992, 440–446.

[27]

O. Seral, S. Gunes Attribute weighting via genetic algorithms for attribute weighted artificial immune system (AWAIS) and its application to heart disease and liver disorders problems

Expert Syst. Appl., 36 (2009), pp. 386-392

[28]

Rahul Karthik Sivagaminathan, Sreeram Ramakrishnan A hybrid approach for feature subset selection using neural networks and ant colony optimization

Expert Syst. Appl., 33 (2007), pp. 49-60

ArticlePDF (228KB)

[29]

S. Tabakhi, P. Moradi, F. Akhlaghian An unsupervised feature selection algorithm based on ant colony optimization

Eng. Appl. Artif. Intell., 32 (2014), pp. 112-123

ArticlePDF (523KB)

[30]

M.A. Tahir, A. Bouridane, F. Kurugollu Simultaneous feature selection and feature weighting using Hybrid Tabu Search/K nearest neighbor classifier

Pattern Recognit. Lett., 28 (2007), pp. 438-446

ArticlePDF (594KB)

[31]

K.C. Tan, E.J. Teoh, Q. Yu, K.C. Goh A hybrid evolutionary algorithm for attribute selection in data mining

Expert Syst. Appl. (2009), pp. 8616-8630

ArticlePDF (1MB)

[32]

A. Tosun, B. Turhan, A.B. Bener Feature weighting heuristics for analogy-based effort estimation models

Expert Syst. Appl., 36 (2009), pp. 10325-10333

ArticlePDF (671KB)

[33]

I. Triguero, J. Derrac, S. Garca, F. Herrera Integrating a differential evolution feature weighting scheme into prototype generation

Neurocomputing, 97 (2012), pp. 332-343

ArticlePDF (804KB)

[34]

Dietrich Wettschereck, David W. Aha, Takao Mohri A review and empirical evaluation of feature weighting methods for a class of lazy learning algorithms

Artif. Intell. Rev., 11 (1997), pp. 273-314

[35]

B. Xue, M. Zhang, W.N. Browne Particle swarm optimisation for feature selection in classification: novel initialisation and updating mechanisms

Appl. Soft Comput., 18 (2013), pp. 261-276

[36]

Zhi-Min Yang, Jun-Yun He, Yuan Hai Shao Feature selection based on linear twin support vector machine

Proc. Comput. Sci., 17 (2013), pp. 1039-1046

ArticlePDF (2MB)

[37]

J.Y. Yeh, T.H. Wu, C.W. Tsao Using data mining techniques to predict hospitalization of hemodialysis patients

Decis. Support Syst., 50 (2) (2011), pp. 439-448

ArticlePDF (686KB)

[38]

Y. Zhang, A. Yang, C. Xiong, T. Wang, Z. Zhang Feature selection using data envelopment analysis

Knowl.-Based Syst., 64 (2014), pp. 70-80

ArticlePDF (761KB)

[39]

Mingyuan Zhao, Chong Fu, Luping Ji, Ke Tang, Mingtian Zhou Feature selection and parameter optimization for support vector: a new approach based on genetic machines algorithm with feature chromosomes

Expert Syst. Appl., 38 (5) (2011), pp. 5197-5204

ArticlePDF (511KB)

[40]

Wenzhi Zhu, Si Gangquan, Zhang Yanbin, Wang Jingcheng Neighborhood effective information ratio for hybrib feature evaluation and selection

Neurocomputing, 99 (2013), pp. 25-37

ArticlePDF (893KB)

[41]

Zexuan Zhu, Yew-soon Ong, Manoranjan Dash Wrapper-filter feature selection algorithm using a memetic framework

IEEE Trans. Syst., Man, Cybern., 37 (2007), pp. 70-76

[42]

Alexandros Kalousis, Julien Prados, Melanie Hilario Stability of feature selection algorithms: a study on high-dimensional spaces

Knowl. Inf. Syst., 12 (1) (2007), pp. 95-116