matlab代码
% 信号处理
% 系统分析
close all;
clear all;
%二阶系统
% wn:无阻尼固有频率 rad/s
% zeta:阻尼系数
wn = 200;
zeta = 0.707;
num1=[wn^2];
num2 = [2*zeta*wn,wn^2];
den = [1,2*zeta*wn,wn^2];
sys1 = tf(num1,den);
%一般二阶系统
sys2 = tf(num2,den);
%带零点的二阶系统
rs1 = step(sys1);
rs2 = step(sys2);
dt = 0.001;
t = 0:dt:0.05;
si = ones(length(t),1);
rs3 = lsim(sys1,si,t,0);
rs4 = lsim(sys2,si,t,0);
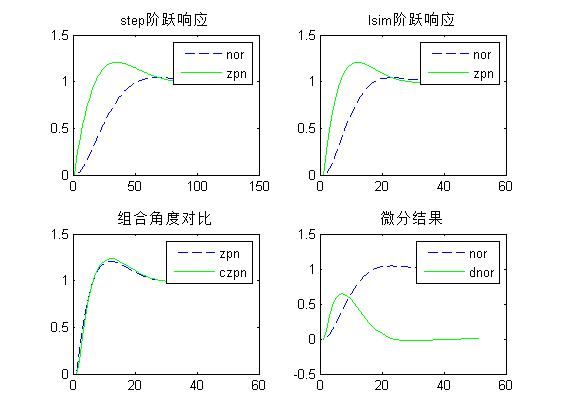
figure
subplot(221)
plot(rs1,'--b');
hold on
plot(rs2,'-g');
legend('nor','zpn'); %normal, zero plus normal
title('step阶跃响应');
subplot(222)
plot(rs3,'--b');
hold on
plot(rs4,'-g');
legend('nor','zpn');
title('lsim阶跃响应')
tau = 2*zeta/wn;
x1 = tau*(rs3-[0;rs3(1:end-1)])/dt;
x2 = rs3;
xt = x1+x2;
% figure
subplot(223);
plot(rs4,'--b');
hold on
plot(xt,'-g');
legend('zpn','czpn');
title('组合角度对比')
subplot(224);
plot(rs3,'--b');
hold on
plot(x1,'g');
legend('nor','dnor');
title('微分结果')
figure
subplot(211)
[z,p] = tf2zp(num1,den);
zplane(z,p);
title('nor零极点图');
subplot(212)
[z,p] = tf2zp(num2,den);
zplane(z,p);
title('zpn零极点图');
%%
%计算幅频相频响应
w = logspace(-4,4,400);
% w = linspace(-2pi,2pi,512);
h1 = freqs(num1,den,w); %函数中的w对应单位rad/s
% h1 = freqz(num1,den);
h2 = freqs(num2,den,w);
figure
subplot(221)
% plot(abs(h1));
loglog(w,abs(h1));
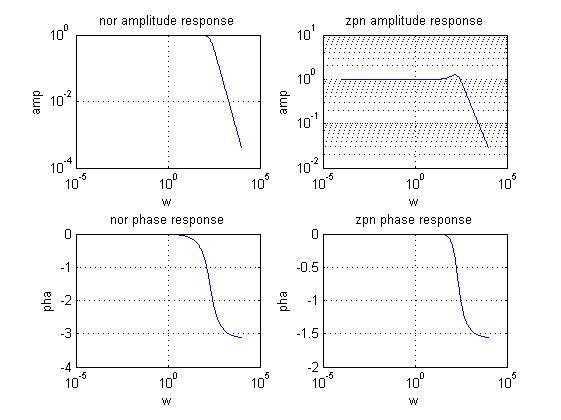
title('nor amplitude response')
ylabel('amp');
xlabel('w');
grid on
subplot(223)
semilogx(w,angle(h1));
title('nor phase response')
ylabel('pha');
xlabel('w');
grid on
subplot(222)
% plot(abs(h2));
loglog(w,abs(h2));
title('zpn amplitude response')
ylabel('amp');
xlabel('w');
grid on
subplot(224)
% plot(angle(h2));
semilogx(w,angle(h2));
title('zpn phase response')
ylabel('pha');
xlabel('w');
grid on
dmag = abs(h2)./abs(h1);
figure
% subplot(211)
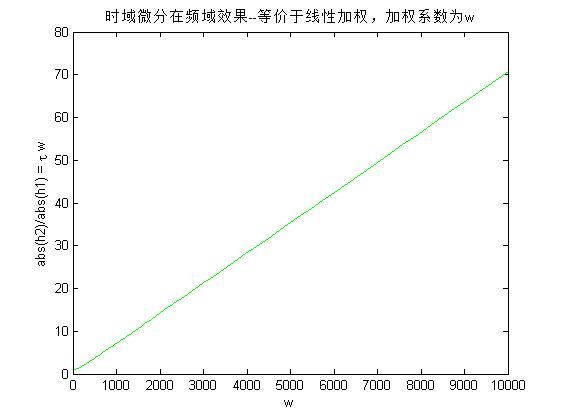
plot(w,dmag,'g');
xlabel('w');
ylabel('abs(h2)/abs(h1) = \tau w')
title('时域微分在频域效果--等价于线性加权,加权系数为w')
disp(['计算出来的\tau等于' num2str((dmag(end)-dmag(1))/(w(end)-w(1)))]);
disp(['实际的\tau值等于' num2str(2*zeta/wn)]);
% subplot(212)
% semilogx(w,dmag);
% 其实真的可以用bode图还绘制,比较方便
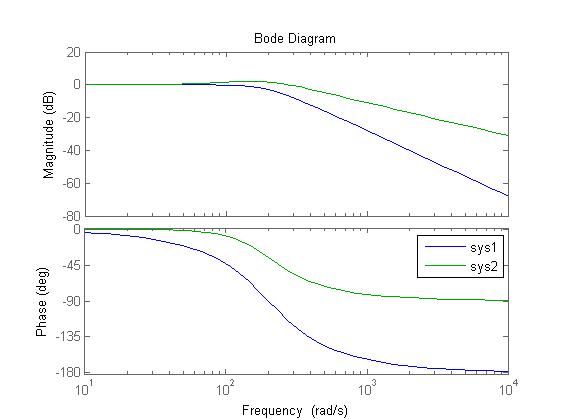
figure
bode(sys1);
hold on
bode(sys2);
legend('show');
% figure
% w = logspace(-1,4,100);
% [mag1,phase1,wout1] =bode(sys1,w);
% [mag2,phase2,wout2] =bode(sys2,w);
%
% dmag = mag2(1,1,:)-mag1(1,1,:);
% plot(w,dmag(1,1,:),'b');
% hold on
% dmagdb = 20*log10(dmag);
% plot(w,dmagdb,'g');
% you can convert the magnitude from absolute units to decibels using:
% magdb = 20*log10(mag)
% c2d
% figure
% pzmap(sys1);
% figure
% pzmap(sys2);
%%
%*******************************************************************
% tf默认的a,b里面的顺序和filter,zplane,impz里面的不同
% 连续域即s域一般是从高到底,离散域是从低到高,变量是z^(-1),因此写的a,b不同
% 连续域的冲激响应用impulse,离散域用impz
% step,dstep
% 连续域的响应可以用lsim,离散域用dlsim,
% freqs,freqz
%%
%************************************************************
%二阶系统时域分析的单位阶跃、单位脉冲、单位斜坡响应
% syms s zeta
% zeta = 0.707; num = [16]; den =[1 8zeta 16];
% p = roots(den);
% sys = tf(num,den);
% t=0:0.01:3;
% figure(1)
% impulse(sys,t);grid
% xlabel('t');ylabel('c(t)');title('impulse response');
% figure(2)
% step(sys,t);grid
% xlabel('t');ylabel('c(t)');title('step response');
% figure(3)
% u=t;
% lsim(sys,u,t,0);grid
% xlabel('t');ylabel('c(t)');title('ramp response');
%
% % 一阶系统时域分析
% syms s t
% num = [1];den=[5,1];
% sys = tf(num,den);
% C = ilaplace((1/(5s+1))(1/s),s,t)
%
%
% % feedback
% %
% % dcgain()
%
% %conv函数用来求解多项式的乘积
% %例如(s+1)(s^2+3s+1)
% % 利用conv([1 1][1 3 1])
% % 可得为[1 4 4 1],即s3+4s2+4s+1
%
% % lsim
%
% % initial(sys,x0)
% % sys = ss(A,B,C,D)
%
% % spline
% % zpk(z,p,k)
%
% freqz
% impz(b,a) %计算单位脉冲响应
% impz(b,a,n)
% filter(b,a,x);
% filtic
% zplane
% pzmap(sys)
% grpdelay