数据拟合方法

数据拟合方法
　　曲线拟合也称为曲线逼近，它和插值函数有一些区别，只要求拟合的曲线合理的反应数据的基本趋势，而并不要求曲线一定经过数据点。曲线拟合有几种不同的判别准则，如使偏差的绝对值之和最小、使偏差的最大绝对值最小和使偏差的平方和最小（即最小二乘法）。最常用的方法是最后一种。
1. polyfit(X,Y,N)函数和polyval函数
1.1 polyfit(X,Y,N)函数
　　多项式曲线拟合。
1.1.1语法
p = polyfit(x,y,n) 返回阶数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（在最小二乘方式中）。p 中的系数按降幂排列，p 的长度为 n+1。
$p(x)=p_1{x}^n+p_2{x}^{n-1}+...+p_{n}x+p_{n+1}$

1） p = polyfit(x,y,n) 返回阶数为 n 的多项式 p(x) 的系数
2）[p,S] = polyfit(x,y,n) 返回一个结构体 S，后者可用作 polyval 的输入来获取误差估计值。
3） [p,S,mu] = polyfit(x,y,n) 返回值mu是二元素向量，表示预测值误差的均值mean(x)和方差std(x)分布

说明：matlab 实现polyfit函数使用的是最小二乘+QR矩阵分解算法，所以以n阶拟合的时候，n应该不大于length(x)。
1.2 polyval函数
对应多项式拟合，多项式求值函数。
1.2.1 语法

y = polyval(p,x); 返回拟合后多项式的值

[y,delta] = polyval(p,x,S)
使用 polyfit 生成的可选输出结构体 S 来生成误差估计值 delta。delta 是使用 p(x) 预测 x 处的未来观测值时的误差标准差估计值。如果 p 中的系数是 polyfit 计算的最小二乘估计值，polyfit 数据输入中的误差呈独立正态分布，并拥有常量方差，则 y±delta 至少包含 x 处 50% 的未来观测值。

y = polyval(p,x,[],mu)或[y,delta] =polyval(p,x,S,mu)
使用 $x_1=(x-{\mu }_1)/{\mu }_2$ 取代 x。在此方程中， ${\mu }_1$=mean(x) 且 ${\mu }_2$=std(x)。中心化和缩放参数 mu = [μ1,μ2] 是由 polyfit 计算的可选输出。

结合polyfit的例子，可以尝试将拟合曲线画出来
1.3 示例

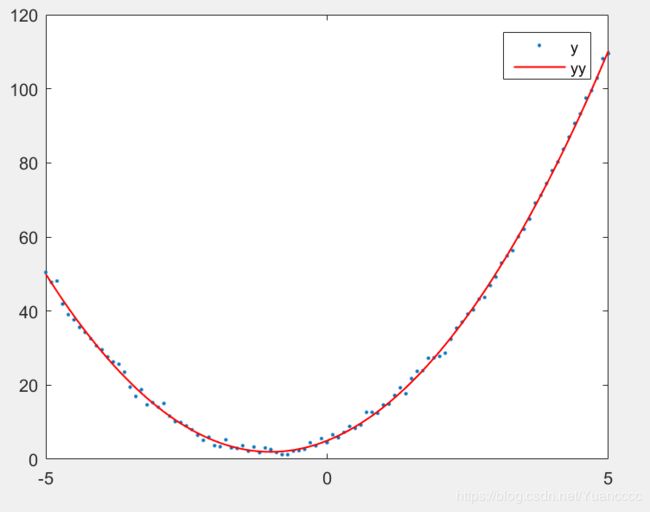
x = (-5:0.1:5);
y = 3*x.^2+6*x + 5 + randn(size(x));
p,S=polyfit(x,y,2)
yy = polyval(p,x); 
plot(x,y,'.');
hold on;
plot(x,yy,'r','LineWidth',1);
legend('y','yy');

运行结果：

>   p =
>        25.7141   17.4310    5.1192
>     S = 
>             R: [3x3 double]
>            df: 98
>         normr: 9.8892
>     mu =
>         0.0000
>         2.9300

结果说明：
（1）p - 最小二乘拟合多项式系数（向量）
（2）S - 误差估计结构体（结构体）
误差估计结构体。此可选输出结构体主要用作 polyval 函数的输入，以获取误差估计值。S 包含以下字段：

字段	说明
R	Vandermonde 矩阵 x 的 QR 分解的三角因子
df	自由度
normr	残差的范数

(3)mu - 中心化值和缩放值(二元素向量)
中心化值和缩放值，以一个二元素向量形式返回。mu(1) 为 mean(x)，并且 mu(2) 为 std(x)。这些值以单位标准差将 x 中的查询点的中心置于零值处。
使用 mu 作为 polyval 的第四个输入以计算 p 在缩放点 (x - mu(1))/mu(2) 处的解。
2、 fittype函数和fit函数
满足自定义复杂的拟合公式。
使用fittype函数可以自定义拟合函数，可以满足线性拟合和非线性拟合。
Fittype函数具有很灵活的配置，基本满足各种复杂场景，有相应的cftool工具箱。
2.1 fittype函数
满足自定义复杂的拟合公式。
使用fittype函数可以自定义拟合函数，可以满足线性拟合和非线性拟合。
2.1.1语法
1）

aFittype = fittype(libraryModelName)
通过指定库模型名称来构造拟合类型。
构造库模型rat33的拟合类型（分子和分母的第三度的有理模型）。

例子：f = fittype('rat33')

f = 
     General model Rat33:
     f(p1,p2,p3,p4,q1,q2,q3,x) = (p1*x^3 + p2*x^2 + p3*x + p4) /
               (x^3 + q1*x^2 + q2*x + q3)

2）

aFittype = fittype(expression)

为MATLAB®表达式指定的模型创建拟合类型。

例子： ft = fittype({'x','sin(x)','1'})

ft = 
     Linear model:
     ft(a,b,c,x) = a*x + b*sin(x) + c

加系数说明：

 ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})

> ft3 = 
>      Linear model:
>      ft3(a1,a2,x) = a1*cos(x) + a2

3）

aFittype = fittype(expression,Name,Value)
使用由一个或多个Name，Value对参数指定的其他选项构造fit类型。

构造自定义非线性模型的拟合类型，指定与问题相关的参数和自变量。
构造自定义非线性模型的拟合类型，将n指定为与问题相关的参数，将u指定为自变量。

g = fittype('a*u+b*exp(n*u)',...
            'problem','n',...
            'independent','u')

g = 
     General model:
     g(a,b,n,u) = a*u+b*exp(n*u)

构造自定义非线性模型的拟合类型，将时间指定为自变量。

g = fittype('a*time^2+b*time+c','independent','time','dependent','height')
g = 
     General model:
     g(a,b,c,time) = a*time^2+b*time+c

构造适合某些数据的对数拟合类型，使用拟合类型创建拟合，并绘制拟合。

x = linspace(1,100);  
y = 5 + 7*log(x);
myfittype = fittype('a + b*log(x)',...
    'dependent',{'y'},'independent',{'x'},...
    'coefficients',{'a','b'})
myfit = fit(x',y',myfittype)
plot(myfit,x,y)

运行结果：

myfittype = 
     General model:
     myfittype(a,b,x) = a + b*log(x)
myfit = 
     General model:
     myfit(x) = a + b*log(x)
     Coefficients (with 95% confidence bounds):
       a =           5  (5, 5)
       b =           7  (7, 7)

4）

aFittype = fittype(linearModelTerms)
为自定义线性模型创建拟合类型，其中的术语由linearModelTerms中的字符向量表达式的单元格数组指定。
要使用线性拟合算法，请指定术语的单元格数组。

确定输入fittype所需的线性模型项：a * x + b * sin（x）+ c。 该模型在a，b和c中是线性的。 它有三个项x，sin（x）和1（因为c = c * 1）。 要指定此模型，请使用此单元格数组：LinearModelTerms = {‘x’，‘sin（x）’，‘1’}。

使用线性模型术语的单元格数组作为fittype的输入。

ft = fittype({'x','sin(x)','1'})
ft = 
     Linear model:
     ft(a,b,c,x) = a*x + b*sin(x) + c

再次创建拟合类型并指定系数名称。

ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})
ft3 = 
     Linear model:
     ft3(a1,a2,x) = a1*cos(x) + a2

5）

aFittype = fittype(linearModelTerms,Name,Value)
使用由一个或多个Name，Value对参数指定的其他选项构造fit类型。

再次创建拟合类型并指定系数名称。

ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})
ft3 = 
     Linear model:
     ft3(a1,a2,x) = a1*cos(x) + a2

7）

aFittype = fittype(anonymousFunction)
为anonymousFunction指定的模型创建适合类型。

使用匿名函数创建适合类型。

g = fittype( @(a, b, c, x) a*x.^2+b*x+c )

使用匿名函数创建拟合类型，并指定独立参数和从属参数。

g = fittype( @(a, b, c, d, x, y) a*x.^2+b*x+c*exp(...
 -(y-d).^2 ), 'independent', {'x', 'y'},...
     'dependent', 'z' );

使用匿名函数为曲面创建拟合类型，并指定独立参数和相关参数，以及稍后在调用fit时指定的问题参数。

g = fittype( @(a,b,c,d,x,y) a*x.^2+b*x+c*exp( -(y-d).^2 ), ...
        'problem', {'c','d'}, 'independent', {'x', 'y'}, ...
        'dependent', 'z' ); 

8）

aFittype = fittype(anonymousFunction,Name,Value)
使用由一个或多个Name，Value对参数指定的其他选项构造fit类型。

使用匿名函数将工作空间数据传递到fittype和fit函数。

创建并绘制S形曲线。 在后面的步骤中，您可以拉伸并移动此曲线以适合某些数据。
2.2 fit函数
将曲线或曲面拟合成数据
2.2.1 语法
1）

fitobject = fit(x,y,fitType)
创建适合于对数据x和y由指定的型号fitType。

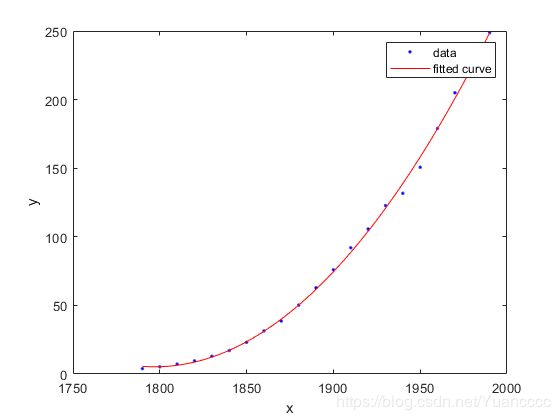
加载一些数据，适合于变量二次曲线cdate和pop，并绘制拟合和数据。

load census;
f = fit（cdate，pop，'poly2'）

f =
线性模型 Poly2：
f（x）= p1 * x ^ 2 + p2 * x + p3
系数（95％置信区间）：
p1 = 0.006541（0.006124，0.006958）
p2 = -23.51（-25.09，-21.93）
p3 = 2.113e + 04（1.964e + 04,2.226e + 04）

plot（F，cdate，pop）

2)

fitobject = fit([x,y],z,fitType)
创建一个表面拟合到数据中的载体x，y和z。

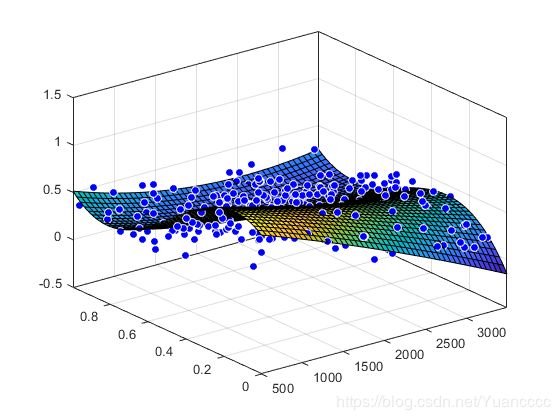
加载一些数据并拟合 2 x度和3 度的多项式曲面y。绘制适合度和数据。

load franke 
sf = fit（[x，y]，z，'poly23'）

线性模型Poly23：
sf（x，y）= p00 + p10 * x + p01 * y + p20 * x ^ 2 + p11 * x * y + p02 * y ^ 2 + p21 * x ^ 2 * y
+ p12 * x * y ^ 2 + p03 * y ^ 3
系数（95％置信区间）：
p00 = 1.118（0.9149,1.321）
p10 = -0.0002941（-0.000502，-8.623e-05）
p01 = 1.533（0.7032,2.364）
p20 = -1.966e-08（-7.084e-08,3.1552e-08）
p11 = 0.0003427（-0.0001009,0.0007863）
p02 = -6.951（-8.421，-5.481）
p21 = 9.563e-08（6.276e-09,1.85e-07）
p12 = -0.0004401（-0.0007082，-0.0001721）
p03 = 4.999（4.082,5.917）

plot(sf,[x,y],z)