PyTorch (莫烦)中
4.2 RNN(一般是用于时间序列的数据)
循环神经网络让神经网络有了记忆, 对于序列话的数据,循环神经网络能达到更好的效果.
几个缺点:
[1] 梯度弥散(消失)反向传播时 W<1 每次误差乘以小于1的数,就会逐渐的趋于0导致没有误差
[2] 梯度爆炸 W>1 每次误差乘以大于1的数,就会逐渐的趋于无穷大
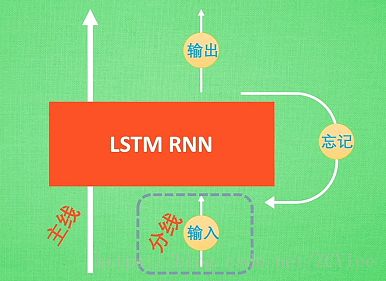
(1)LSTM RNN(可以有更好的结果)
应用:
(1)分类:(mnist 手写数字识别)
对于图片,怎样看成时间序列的数据呢,可将其看成从上到下的读图,第一个时间点读第一行的像素信息,直到最后一行读完
import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28 # rnn time step / image height 每次读一行像素点,一共28行,就有28个时间点
INPUT_SIZE = 28 # rnn input size / image width 每行有28个像素点 所以输入信息为28
LR = 0.01 # learning rate
DOWNLOAD_MNIST = False # set to True if haven't download the data
# Mnist digital dataset
train_data = dsets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()
# Data Loader for easy mini-batch return in training
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# convert test data into Variable, pick 2000 samples to speed up testing
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy().squeeze()[:2000] # covert to numpy array
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit 64个神经元
num_layers=1, # number of rnn layer 一层神经元(比较简单)
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
) #if (time_step, batch, input_size) batch_first=False
self.out = nn.Linear(64, 10) # 64:神经元的输出做输入 10:10个分类作为输出
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :]) #(batch,time_step,input) 选取看完整张图片之后的时间点,再进行训练
return out
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted 数字标签是多少就是多少
#比如数字标签是7 ,不会显示0111
# training and testing
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')运行结果:
CNN :
RNN:
CNN的效果比较好
(2)回归 用 RNN 来及时预测时间序列,这次是真正意义上使用RNN,RNN是在每一个时间都有输出的,比较一下和真实数据的差别
(input:sin output: cos 从sin向着cos 趋近)
import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
TIME_STEP = 10 # rnn time step
INPUT_SIZE = 1 # rnn input size 只有y值
LR = 0.02 # learning rate
# show data
steps = np.linspace(0, np.pi*2, 100, dtype=np.float32)
x_np = np.sin(steps) # float32 for converting torch FloatTensor
y_np = np.cos(steps)
plt.plot(steps, y_np, 'r-', label='target (cos)')
plt.plot(steps, x_np, 'b-', label='input (sin)')
plt.legend(loc='best')
plt.show()
class RNN(nn.Module): #这节用RNN即可
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.RNN(
input_size=INPUT_SIZE,
hidden_size=32, # rnn hidden unit 32个神经元
num_layers=1, # number of rnn layer 一层神经元
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(32, 1) #32个输入,接着某一时刻(32个神经元)的输出;1个输出 与时间点对应的y值
def forward(self, x, h_state): # 因为 hidden state 是连续的, 所以我们要一直传递这一个 state
# x (batch, time_step, input_size)
# h_state (n_layers, batch, hidden_size)
# r_out (batch, time_step, hidden_size)
r_out, h_state = self.rnn(x, h_state) #h_sate 相当于对之前的记忆
outs = [] # save all predictions 保存所有时间点的预测值
for time_step in range(r_out.size(1)): # pytorch特有的动态计算图 很方便 tensorflow 中没有
outs.append(self.out(r_out[:, time_step, :])) #对每一个时间点计算output,每一次的输出都要Linear层的加工
return torch.stack(outs, dim=1), h_state #输出是一个list的形式,把它变成tensor(torch.stack)压在一起
#h_state 返回值传入到下一次forward中 4.3 自编码Autoencode(非监督性学习)
神经网络也能进行非监督学习, 只需要训练数据, 不需要标签数据. 自编码就是这样一种形式. 自编码能自动分类数据, 而且也能嵌套在半监督学习的上面, 用少量的有标签样本和大量的无标签样本学习.
对于大量数据的任务,可以进行先压缩,提取主要特征,通过神经网络的学习,后进行解压的操作。
主要在编码,通过使用编码器,即可压缩,得到原数据的主要精髓。
只有输入的白色X,通过压缩,神经网络,解压得到黑色X,然后通过对比黑白 X ,求出预测误差, 进行反向传递, 逐步提升自编码的准确性。训练好的自编码中间这一部分就是能总结原数据的精髓. 可以看出, 从头到尾, 我们只用到了输入数据 X, 并没有用到 X 对应的数据标签, 所以也可以说自编码是一种非监督学习. 到了真正使用自编码的时候. 通常只会用到自编码前半部分.
优点:自编码可以像PCA一样对数据降维。
4.3.1 编码器 Encode
这 部分也叫作 encoder 编码器. 编码器能得到原数据的精髓, 然后我们只需要再创建一个小的神经网络学习这个精髓的数据,不仅减少了神经网络的负担, 而且同样能达到很好的效果.
这是一个通过自编码整理出来的数据, 他能从原数据中总结出每种类型数据的特征, 如果把这些特征类型都放在一张二维的图片上, 每种类型都已经被很好的用原数据的精髓区分开来. 如果你了解 PCA 主成分分析, 再提取主要特征时, 自编码和它一样,甚至超越了 PCA. 换句话说, 自编码 可以像 PCA 一样 给特征属性降维.
4.3.2 解码器 Decode
至于解码器 Decoder, 我们也能那它来做点事情. 我们知道, 解码器在训练的时候是要将精髓信息解压成原始信息, 那么这就提供了一个解压器的作用, 甚至我们可以认为是一个生成器 (类似于GAN). 那做这件事的一种特殊自编码叫做 variational autoencoders.
4.3.3 通过自编码实现手写数字分类
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy as np
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005 # learning rate
DOWNLOAD_MNIST = False
N_TEST_IMG = 5
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[2].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[2])
plt.show()
# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(28*28, 128), #28*28:图像大小 128:神经元
nn.Tanh(),
nn.Linear(128, 64), #压缩到64
nn.Tanh(),
nn.Linear(64, 12), #压缩到12
nn.Tanh(),
nn.Linear(12, 3), # compress to 3 features which can be visualized in plt 压缩到3 为了方便三维显示
)
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.Tanh(),
nn.Linear(12, 64),
nn.Tanh(),
nn.Linear(64, 128),
nn.Tanh(),
nn.Linear(128, 28*28),
nn.Sigmoid(), # compress to a range (0, 1) 将数据放到(0,1)的范围内
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return encoded, decoded #返回这两个值后 可以在显示时使用
autoencoder = AutoEncoder()
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()
# initialize figure
f, a = plt.subplots(2, N_TEST_IMG, figsize=(5, 2))
plt.ion() # continuously plot
# original data (first row) for viewing
view_data = train_data.train_data[:N_TEST_IMG].view(-1, 28*28).type(torch.FloatTensor)/255.
for i in range(N_TEST_IMG):
a[0][i].imshow(np.reshape(view_data.data.numpy()[i], (28, 28)), cmap='gray'); a[0][i].set_xticks(()); a[0][i].set_yticks(())
for epoch in range(EPOCH):
for step, (x, b_label) in enumerate(train_loader):
b_x = x.view(-1, 28*28) # batch x, shape (batch, 28*28)
b_y = x.view(-1, 28*28) # batch y, shape (batch, 28*28) 其实还是X 只不过为了和decoder的结果比较
encoded, decoded = autoencoder(b_x)
loss = loss_func(decoded, b_y) # mean square error
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 100 == 0:
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy())
# plotting decoded image (second row)
_, decoded_data = autoencoder(view_data)
for i in range(N_TEST_IMG):
a[1][i].clear()
a[1][i].imshow(np.reshape(decoded_data.data.numpy()[i], (28, 28)), cmap='gray')
a[1][i].set_xticks(()); a[1][i].set_yticks(())
plt.draw(); plt.pause(0.05)
plt.ioff()
plt.show()
# visualize in 3D plot
view_data = train_data.train_data[:200].view(-1, 28*28).type(torch.FloatTensor)/255.
encoded_data, _ = autoencoder(view_data)
fig = plt.figure(2); ax = Axes3D(fig)
X, Y, Z = encoded_data.data[:, 0].numpy(), encoded_data.data[:, 1].numpy(), encoded_data.data[:, 2].numpy()
values = train_data.train_labels[:200].numpy()
for x, y, z, s in zip(X, Y, Z, values):
c = cm.rainbow(int(255*s/9)); ax.text(x, y, z, s, backgroundcolor=c)
ax.set_xlim(X.min(), X.max()); ax.set_ylim(Y.min(), Y.max()); ax.set_zlim(Z.min(), Z.max())
plt.show()