C语言关键路径实现
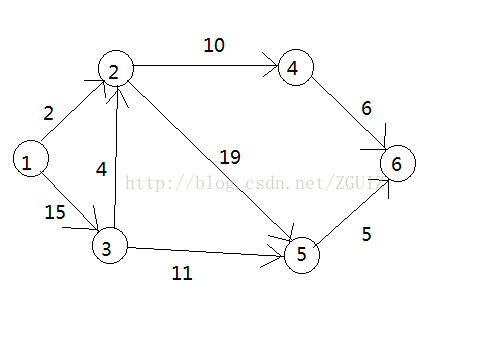
在工程中,要估算工程完成最短时间,就是要找到一条从源点到汇点的带权路劲长度最长的路径,成为关键路径。
确定关键路径的四个描述量:
1. 事件vi的最早发生时间ve(i):
进入世界vi的每一活动都结束,vi才有可发生,所以ve(i)是从源点到vi的最长路径长度。其中v0一般为0.
2. 事件vi的最迟发生时间:
事件vi的发生不得延误vi的每一后继事件的最迟发生时间。为了不延误工期,vi的最迟时间不得迟于其后继事件vk的最迟发生时间减去活动
3. 活动ai=
只有事件vj发生了,活动ai才能开始。所以活动ai的最早开始时间等于时间vj的最早发生时间ve(j)。
4. 活动a i=
活动a i的开始时间需要保证不延误时间vk的最迟发生时间。所以活动a i的最晚开始时间l(i)等于时间vk的最迟发生时间vl(k)减去活动ai的持续时间wj,k。
对于关键活动而言,e(i)=l(i)。对于非关键活动,l(i)-e(i)的值是该工程的期限余量,此范围内的适度延误不会影响整个工程的工期。
(以上引用课本原文)
下面是实现代码:
预定义和类型定义:
#define OK 1
#define ERROR 0
#define MVNum 100
typedef int Status;
typedef char VerTexType;
typedef int OtherInfo;
typedef struct StackNode{
int data;
StackNode *next;
}StackNode, *StackList;
typedef struct ArcNode{
int adjvex;
ArcNode *nextarc;
OtherInfo weight;
}ArcNode;
typedef struct VNode{
VerTexType data;
ArcNode *firstarc;
}VNode, AdjList[MVNum];
typedef struct{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;
创建图、栈和拓扑排序:
int indegree[MVNum] = { 0 };
StackList InitStack(StackList &S)
{
S = NULL;
return S;
}
StackList Push(StackList S, int e)
{
StackList p;
p = (StackNode *)malloc(sizeof(StackNode));
p->data = e;
p->next = S;
S = p;
return S;
}
StackList Pop(StackList S, int *e)
{
StackList p;
p = S;
if (!p)
return ERROR;
*e = p->data;
S = S->next;
free(p);
return S;
}
int LocateVex(ALGraph *G, VerTexType v)
{
int i;
for (i = 0; i < (G->vexnum); i++)
{
if (v == G->vertices[i].data)
return i;
}
}
void CreateUDG(ALGraph *G)
{
int i, j, k;
OtherInfo w;
VerTexType v1, v2;
ArcNode *p1;
printf("输入总节点数和总边数:");
scanf("%d %d", &G->vexnum, &G->arcnum);
fflush(stdin);
printf("输入各个节点的值:");
for (i = 0; i < G->vexnum; i++)
{
scanf("%c", &G->vertices[i].data);
G->vertices[i].firstarc = NULL;
}
for (k = 0; k < G->arcnum; k++)
{
fflush(stdin);
printf("输入一条边的两个节点以及边的权值:");
scanf("%c %c %d", &v1, &v2, &w);
i = LocateVex(G, v1);
j = LocateVex(G, v2);
p1 = (ArcNode *)malloc(sizeof(ArcNode));
p1->adjvex = j;
p1->weight = w;
p1->nextarc = G->vertices[i].firstarc;
G->vertices[i].firstarc = p1;
indegree[j]++;
}
}
Status TopologicalSort(ALGraph G, int *topo)
{
int i, m, k;
StackList S;
ArcNode *p;
S = NULL;
for (i = 0; i < G.vexnum; i++)
{
if (!indegree[i])
S = Push(S, i);
}
m = 0;
while (S)
{
S = Pop(S, &i);
topo[m] = i;
++m;
p = G.vertices[i].firstarc;
while (p != NULL)
{
k = p->adjvex;
--indegree[k];
if (indegree[k] == 0)
S = Push(S, k);
p = p->nextarc;
}
}
topo[m] = -1;
if (m < G.vexnum)
return ERROR;
else
return OK;
}
关键路径算法:
Status CriticalPath(ALGraph G)
{
int i, j, k, e, l;
int *ve, *vl;
int topo[MVNum];
ArcNode *p;
ve = (int *)malloc(sizeof(int)*G.vexnum);
vl = (int *)malloc(sizeof(int)*G.vexnum);
if (!TopologicalSort(G, topo))
return ERROR;
for (i = 0; i < G.vexnum; i++)
ve[i] = 0;
for (i = 0; i < G.vexnum; i++)
{
k = topo[i];
p = G.vertices[k].firstarc;
while (p)
{
j = p->adjvex;
if (ve[j] < ve[k] + p->weight)
ve[j] = ve[k] + p->weight;
p = p->nextarc;
}
}
for (i = 0; i < G.vexnum; i++)
vl[i] = ve[G.vexnum - 1];
for (i = G.vexnum - 1; i >= 0; i--)
{
k = topo[i];
p = G.vertices[k].firstarc;
while (p)
{
j = p->adjvex;
if (vl[k]>vl[j] - p->weight)
vl[k] = vl[j] - p->weight;
p = p->nextarc;
}
}
for (i = 0; i < G.vexnum; i++)
{
p = G.vertices[i].firstarc;
while (p)
{
j = p->adjvex;
e = ve[i];
l = vl[j] - p->weight;
if (e == l)
printf("%c->%c\n", G.vertices[i].data, G.vertices[j].data);
p = p->nextarc;
}
}
return OK;
}
声明两个数组ve[]和vl[]分别用来记录事件最早发生时间和最晚发生时间。为了避免浪费,本人使用动态分配空间为数组分配空间。然后进行拓扑排序(注意输入原始数据的时候保证最后一个元素是最后一步事件)。之后初始化ve[]为0。
为ve[]赋值:让将topo[]中的第i个元素赋值给k,并让指针p指向k元素的第一条边。当p不为空的时候,判断p边记录的另一个节点事件的最早发生时间是否小于k节点记录事件最早发生时间加上p边的权值,若小于,则将k节点记录事件最早发生时间加上p边的权值赋值给ve[j]。让p指向下一条边。重复本段操作为所有ve[]赋值。
初始化vl[],将其元素全部赋值为ve[G.vexnum-1](工程完成时间,即最后一个项目最早发生时间)。
为vl[]赋值:让topo[i]赋值给k,并让p指向k元素的第一条边。当p不为空的时候,判断p边记录的另一个节点时间的最晚发生时间减去p边的权值是否小于k节点记录事件的最晚发生时间,若小于,则将p边记录的另一个节点时间的最晚发生时间减去p边的权值赋值给vl[k]。让p指向下一条边。重复本段操作为所有vl[]赋值。
判断是否为关键路径:将p指向第i个节点的第一条边。当p不为空的时候让e为ve[i],l为p边记录的另一个节点的事件最晚发生时间减去p边的权值,若e和l相等则输出边的两个顶点。让p指向下一条边。重复本段操作直到检测完所有关键路径。
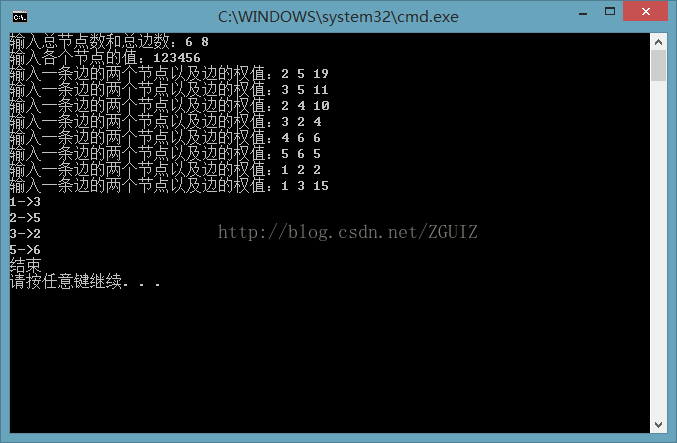
加入main():
int main(void)
{
ALGraph G;
CreateUDG(&G);
if (!CriticalPath(G))
printf("错误\n");
else
printf("结束\n");
return 0;
}