定点数乘法运算：Booth算法（补码一位乘法）C 实现

---

综述

在计算机中参与运算的机器数有两大类：无符号数和有符号数。

下面主要讲解有符号数:

在机器中，数的“正”、“负”号是无法识别的，有符号数用“0”表示正，用“1”表示负号，从而将符号数值化，并通常约定二进制数的最高位是符号位，即符号位放在有效数字的前面，组成有符号数。

有符号数的机器表示有原码、补码、反码和移码。

根据小数点的位置是否固定，在计算机中的有两种数据格式：定点表示和浮点表示。接下来我们将介绍的算法都是定点表示。

有关浮点数的内存存储及介绍请参考我的另一篇博文：
《浮点数在内存中的存储方式与运算陷阱》

定点表示即约定机器数中的小数点位置是固定不变的，小数点不再使用 “ . ” 表示，而是约定它的位置。理论上，小数点位置固定在哪一位都是可以的，但在计算机中通常采用两种简单的约定

• 将小数点的位置固定在数据的最高位之前，一般称为定点小数
• 将小数点的位置固定在数据的最高位之后，一般称为定点整数

定点小数是纯小数，约定小数点位置在符号位之后、有效数值部分最高位之前。
定点整数是纯整数，约定小数点位置在符号位有效数值部分最低位之后。

本文将介绍定点数的乘法运算。

---

定点数的乘法运算

在计算机中，乘法运算由累加和右移操作实现。根据机器数的不同，可分为

• 原码一位乘法
• 补码一位乘法

原码一位乘法的规则比补码一位乘法简单。我们下面主要介绍补码一位乘法（Booth）算法。

---

Booth算法分析

这是一种有符号数的乘法，采用相加和相减操作计算补码数据的乘积。

设 [X]补 = Xs.X1X2···Xn， [Y]补 = Ys.Y1Y2···Yn，则运算规则如下：

• 符号位参与运算，运算的数均以补码表示
• 被乘数一般取双符号位参与运算，部分积取双符号位，初值为0，乘数可取单符号位
• 乘数末尾增设附加位Yn+1，且初值为0
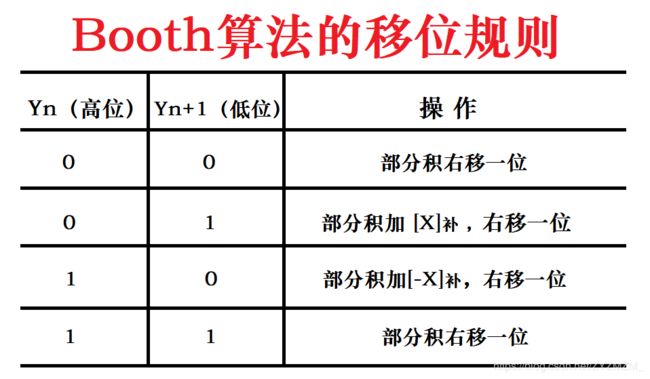
• 根据（Yn，Yn+1）的值来确定操作，具体见下表
• 移位按照补码右移规则进行
• 按照上述算法进行 n+1 步操作，但 n + 1 步不再移位（共进行 n + 1 次累加和 n次右移），仅根据Yn 与 Yn+1 的比较结果做相应的运算。
  

接下来我们分析一个实例：

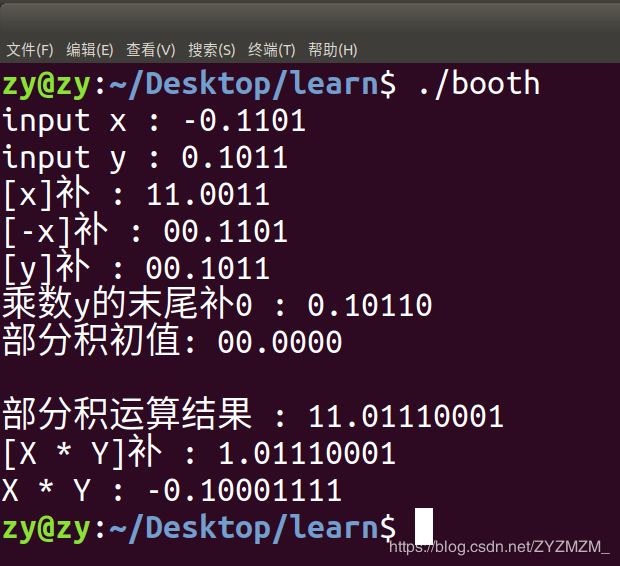
设机器字长为5位（含一位符号位，n = 4），x = -0.1101，y = 0.1101，采用Booth算法求解 x · y。

---

Booth算法的C实现

通过上述分析，我们通过C语言来实现Booth算法。

问题描述：使用纯C实现Booth算法，不允许调用除输入输出外的其他功能库函数。

问题分析：
我们需要完成下述功能：

• 输入x、y，计算出 [X]补、[-X]补、 [Y]补
• 将X改为双符号位数
• 部分积取双符号位，初值为0
• 分割乘数，获取（Yn，Yn+1）的值
• 根据（Yn，Yn+1）的值执行相应操作

完整设计如下：

/**
* Copyright: Copyright(c) 2019
* Created on 26/4/2019
* Author : ZYZMZM
* Version 1.0
* Title : Booth Algorithm
**/

#include 

/* 存储被乘数 x 的补码 */
char xCom[20] = { 0 };

/* 存储 -x 的补码 */
char mxCom[20] = { 0 };

/* 存储乘数 y 的补码 */
char yCom[20] = { 0 };

/* 存储乘数 y 末位增加 0 */
char multiNum[20] = { 0 };

/* 存储部分积的初值 */
char multiSrc[20] = { 0 };

/* 计算字符串长度 */
int length(char* ch)
{
	int len = 0;
	while (*ch != NULL)
	{
		++len;
		++ch;
	}
	return len;
}

/* 拷贝字符串 */
char* copy(char* dest, const char* src)
{
	char* tmp = dest;
	while (*dest++ = *src++) {}
	return tmp;
}

/* 字符串比较 */
int compare(const char* dest, const char* src)
{
	int tmp = 0;
	while (!(tmp = *dest - *src) && *dest && *src)
	{
		dest++;
		src++;
	}
	if (tmp > 0) { return 1; }
	else if (tmp < 0) { return -1; }
	else { return 0; }
}

/* 字符串截取：截取从src中的begin下标到end下标的字符串，结果存储在res中 */
char* intercept(char* src, char *res, int begin, int end)
{
	int i = begin;
	int j = 0;
	while (i <= end)
	{
		res[j] = src[i];
		++j;
		++i;
	}
	return res;
}

/* 右移 */
void mRight(char* src)
{
	int len = length(src);
	int i = len - 1;

	/* 获取小数部分的起始位置 */
	int num = 0;
	char* p = src;
	while (*p != '.')
	{
		++num;
		++p;
	}
	++num;

	/* 将小数后的第一位空出，其余全部后移 */
	for (; i >= num; --i)
	{
		src[i + 1] = src[i];
	}
	++i;
	
	/* 根据正负进行添1 或 添0 */
	if (src[0] == '1')
	{
		src[i] = '1';
	}
	else
	{
		src[i] = '0';
	}
	
}

/* 浮点数加法 */
void Add(char* lhsstr, char *rhsstr, char *result)
{
	int lhsLen = length(lhsstr);
	int rhsLen = length(rhsstr);
	
	/* 对长度较小的数字，在其后补0，目的是为了使两数长度相同 */
	if (lhsLen < rhsLen)
	{
		int diff = rhsLen - lhsLen;
		int i = lhsLen;
		while (diff > 0)
		{
			lhsstr[i] = '0';
			--diff;
			++i;
		}
	}
	else if (lhsLen > rhsLen)
	{
		int diff = lhsLen - rhsLen;
		int i = rhsLen;
		while (diff > 0)
		{
			rhsstr[i] = '0';
			--diff;
			++i;
		}
	}

	/* 拿到最大的长度 */
	int i = lhsLen <= rhsLen ? rhsLen - 1 : lhsLen - 1;
	int j = i;

	/* 进位标志 */
	int flag = 0;

	while (i >= 0)
	{
		/* 小数点跳过 */
		if (lhsstr[i] == '.')
		{
			result[i] = '.';
			--i;
			continue;
		}
		/* 小数点跳过 */
		if (rhsstr[j] == '.')
		{
			result[j] = '.';
			--j;
			continue;
		}

		int lhs = lhsstr[i] - '0';
		int rhs = rhsstr[j] - '0';

		int sum = lhs + rhs;

		if (flag == 1)
		{
			sum += 1;
			flag = 0;
		}
		/* 和为2，则需要进位，存储0，更新进位标志 */
		if (sum == 2) 
		{
			flag = 1;
			sum = 0;
		}
		/* 和为3，即之前有进位，且现在和为2也有进位，即11，存储1，更新进位标志 */
		else if (sum == 3)
		{
			flag = 1;
			sum = 1;
		}
		result[i] = sum + '0';
		--i;
		--j;
	}
}

/* 原码转补码 */
void calComplement(char *origin, char *recv)
{
	/* 负数标志 */
	int isMinus = 0;
	if (origin[0] == '-')
	{
		isMinus = 1;
	}

	char* result = origin;

	/* 原码为负，补码--> 原码变反加一 */
	if (isMinus)
	{
		/* -0.1101  -> 11.xxxx */
		*origin++ = '1';
		*origin++ = '1';

		/* 小数位全部变反 */
		while (*origin != NULL)
		{
			if (*origin == '1')
			{
				*origin = '0';
			}
			else if (*origin == '0')
			{
				*origin = '1';
			}
			++origin;
		}

		/* 加一操作：构造和操作数长度相同的加数，即 11.xxxx + 00.0001 */
		int len = length(result);
		char rhs[20] = { 0 };
		rhs[0] = '0';
		rhs[1] = '0';
		rhs[2] = '.';
		rhs[len - 1] = '1';
		for (int i = len - 2; i > 2; --i)
		{
			rhs[i] = '0';
		}

		Add(result, rhs, recv);  
		return;
	}

	/* 原码为正，补码不改变，但在这里给补码前补0，即 0.1011 --> 00.1011 */
	int len = length(origin);
	for (int i = len - 1; i >= 0; --i)
	{
		origin[i + 1] = origin[i];
	}
	origin[0] = '0';
	copy(recv, origin);
}


/* 补码转原码：最后的结果转换 */
void calOri(char* origin, char* recv)
{
	/* 负数标志 */
	int isMinus = 0;
	if (origin[0] == '1')
	{
		isMinus = 1;
	}

	char* result = origin;
	
	/* 补码的符号位为负 */
	if (isMinus)
	{
		/*
			multiRes : 11.01110001
			X * Y COM : 1.01110001
			X * Y : -0.10001111
		*/

		/*
		** 11.XXXXX --> -0.XXXXX（通过multiRes补码
		** 转换，因为11恰好可用-0，都是两位，直接替换） 
		*/
		*origin++ = '-';
		*origin++ = '0';

		/* 按位取反 */
		while (*origin != NULL)
		{
			if (*origin == '1')
			{
				*origin = '0';
			}
			else if (*origin == '0')
			{
				*origin = '1';
			}
			++origin;
		}

		/* 加一操作 */
		int len = length(result);
		char rhs[20] = { 0 };
		rhs[0] = '0';
		rhs[1] = '0';
		rhs[2] = '.';
		rhs[len - 1] = '1';
		for (int i = len - 2; i > 2; --i)
		{
			rhs[i] = '0';
		}

		Add(result, rhs, recv);
		return;
	}

	/* 补码符号位为正，即原码和补码相同 */
	copy(recv, origin);
}

/* booth算法核心实现 */
void Calculate()
{
	int i = 0;
	char index[20] = { 0 };

	/* 拿到末尾添0的乘数副本 */
	copy(index, multiNum);
	
	/* 计算小数部分起始位置 */
	int num = 0;
	while (index[i] != '.')
	{
		++num;
		++i;
	}

	/* 去掉index的小数点，便于之后进行移位分割 */
	char res[20] = { 0 };
	int len = length(index);
	for (i = num; i < len - 1; ++i)
	{
		index[i] = index[i + 1];
	}
	index[i] = '\0';
	

	i = length(index) - 1;

	/* 首次计算标志，因为首次计算是与部分积初值的计算 */
	int first = 1;

	/* 存储部分积 */
	char multiRes[20] = { 0 };

	while (i - 1 >= 0)
	{
		/* 移位分割，从低位向高位分割，分割首末位置每次同时向高位移动一位 */
		intercept(index, res, i - 1, i); 

		/* 首次是与初值的运算 */
		if (first)
		{
			first = 0;
			if (compare(res, "00") == 0)
			{
				/* 00 --> 初值右移一位 */
				mRight(multiSrc);
			}
			else if (compare(res, "01") == 0)
			{
				/* 01 --> 初值加[x]补，并右移一位 */
				Add(multiSrc, xCom, multiRes);
				mRight(multiRes);
			}
			else if (compare(res, "10") == 0)
			{
				/* 10 --> 初值加[-x]补，并右移一位 */
				Add(multiSrc, mxCom, multiRes);
				mRight(multiRes);
			}
			else if (compare(res, "11") == 0)
			{
				/* 初值右移一位 */
				mRight(multiSrc);
			}
		}
		/* 非首次都是与部分积的运算 */
		else
		{
			/* 00 --> 部分积右移一位 */
			if (compare(res, "00") == 0)
			{
				if (i - 1 != 0)
					mRight(multiRes);
			}
			else if (compare(res, "01") == 0)
			{
				/* 01 --> 部分积加[x]补，并右移一位 */
				Add(multiRes, xCom, multiRes);
				if (i - 1 != 0) 
					mRight(multiRes);
			}
			else if (compare(res, "10") == 0)
			{
				/* 10 --> 部分积加[-x]补，并右移一位 */
				Add(multiRes, mxCom, multiRes);
				if (i - 1 != 0)
					mRight(multiRes);
			}
			else if (compare(res, "11") == 0)
			{
				/* 部分积右移一位 */
				if (i - 1 != 0)
					mRight(multiRes);
			}
		}
		--i;
	}

	/* 部分积运算结果 */
	printf("部分积运算结果 : %s\n", multiRes);
	
	/* 拷贝运算结果，因为它会被下面计算补码时更改，但是计算原码时要用到它 */
	char Ori[20] = { 0 };
	copy(Ori, multiRes);

	/* 通过部分积得到补码 */
	if (multiRes[0] == '1')
	{
		int mlen = length(multiRes);
		i = 0;
		for (; i < mlen - 1; i++)
		{
			multiRes[i] = multiRes[i + 1];
		}
		multiRes[i] = '\0';
	}
	printf("[X * Y]补 : %s\n", multiRes);
	
	/* 通过部分积得到原码 */
	char finalRes[20] = { 0 };
	calOri(Ori, finalRes);
	printf("X * Y : %s\n", finalRes);

}

int main()
{
	char inputx[20] = { 0 };
	char inputy[20] = { 0 };

	printf("input x : ");
	scanf("%s", inputx);
	printf("input y : ");
	scanf("%s", inputy);

	char origin[20] = { 0 };

	// x补码
	copy(origin, inputx);
	calComplement(origin, xCom);
	printf("[x]补 : %s\n", xCom);

	// -x补码
	copy(origin, inputx);
	int lenx = length(origin);
	/* 如果x本身就为负，那么直接将负号去掉即可得到-x */
	if (inputx[0] == '-')
	{
		int i = 0;
		for (; i < lenx - 1; ++i)
		{
			origin[i] = origin[i + 1];
		}
		origin[i] = '\0';
	}
	/* 如果x本身为正，那么添加负号得到-x */
	else
	{
		for (int i = lenx - 1; i >= 0; --i)
		{
			origin[i + 1] = origin[i];
		}
		origin[0] = '-';
	}
	calComplement(origin, mxCom);
	printf("[-x]补 : %s\n", mxCom);

	// y补码
	copy(origin, inputy);
	calComplement(origin, yCom);
	printf("[y]补 : %s\n", yCom);

	// 乘数y的末尾补0
	copy(origin, inputy);
	int leny = length(origin);
	origin[leny] = '0';
	origin[leny + 1] = '\0';
	copy(multiNum, origin);
	printf("乘数y的末尾补0 : %s\n", multiNum);


	// 计算部分积初值
	multiSrc[0] = '0';
	multiSrc[1] = '0';
	multiSrc[2] = '.';
	int len = length(xCom) - 3;
	int i = 0;
	int j = 3;
	for (; i < len; ++i, ++j)
	{
		multiSrc[j] = '0';
	}
	printf("部分积初值: %s\n\n", multiSrc);
	
	/* Booth算法 */
	Calculate();
}

我们输入之前的示例进行验证：

由结果可知，我们的计算是正确的。