关于 Trie树 前缀查询问题的补充(实现非遍历前缀模式匹配)
之前我们有介绍Trie树的基本理论与C++操作实现:
《C++高级数据结构算法 | Tire树(字典树、前缀树)》
今天重点讲解一下有关Tire树的模式匹配的问题。我们在之前的博文中对于模式匹配问题只是简单的输出了指定前缀拥有的单词总数,如果我们想要实现真正的按指定前缀打印字符,那么我们该怎么做呢?
本篇文章就来补充讲解此问题。
文章目录
- Tire树的模式匹配问题的设计思路
- 代码补充与更新部分
- Tire树节点定义更新
- 插入主函数
- 插入更新函数
- 删除主函数
- 删除更新函数
- 实现非遍历前缀模式匹配
- 坑爹的内存泄露检查之路
- 功能测试 - 《哈利波特》文章单词匹配
Tire树的模式匹配问题的设计思路
我们知道Tire树的核心算法就是前缀匹配,但是我们上篇博文仅仅实现了对于指定前缀的次数输出,我们实际中是需要输出具体的单词的,那么如何实现呢?
参考了一下网上其他博文,没有什么收获,因为大家的实现方式、数据结构各异,不具有参考价值。
自己刚开始是准备根据指定的前缀对Tire树进行一个匹配遍历,但是发现这种方式的算法设计过于复杂,因为每个结点都有next域,我们需要判断其中哪些是有效的,而且这些有效的next域中也存在next域,递归遍历层次太深,很容易导致堆栈溢出,迭代算法设计太头疼~
下面谈谈我的设计思路:
首先我们想一下之前我们如何实现指定前缀的次数查询的:对Trie树节点添加一个count成员,在插入时对其进行更新即可。
那么同样的思路,我们要实现对于具体的单词的输出,我们何不再建立一个空间用来存储以该结点到根组成的字符串为前缀的所有单词呢?可能这种算法并不是最优算法,主要是因为结点的空间消耗又增加了,但是我们将树建成后,对于任一指定前缀的单词匹配都是O(1)的时间,时间效率是非常可观的,尤其是在海量数据的情境中,效率非常之高。
当然,我们既然给结点添加了一个成员,因此在删除一个单词时,我们就需要将该路径上结点中所存储的该单词删除掉。
接下来简单谈一下思路:
- 插入操作:插入操作的基本代码不变,我们需要增设一个更新标志位,只有新插入的单词进行了结点开辟时,我们才会在调用尾部的更新函数进行更新,具体就是从最后一个字符结点开始,依次向根回溯,把插入的单词添加到对应的容器中。
- 删除操作:删除操作的基本代码不变,我们只在首部添加一个更新函数即可,就是从最后一个字符结点开始,依次向根回溯,把待删除的单词从每个结点中的容器里删除即可。
代码补充与更新部分
Tire树节点定义更新
class TrieNode
{
public:
bool isWord;
char word;
int count;
TrieNode* next[MaxBranchNum];
/* 存储从根到该结点处组成的字符串作为前缀的单词集合*/
vector<string> priString;
······
};
插入主函数
void insert(string str)
{
if (str.length() == 0)
return;
/* curNode 指向Trie树的根节点 */
TrieNode* curNode = pRoot;
/* 设置更新标志位,只有新插入的单词进行了结点开辟才会置为true */
bool isUpdate = false;
/* 遍历待插入单词的每个字符,并进行插入 */
for (char str_ch : str)
{
/* 在路径中该字符结点存在,更新count域,继续向子节点遍历 */
if (curNode->next[str_ch] != nullptr)
{
curNode = curNode->next[str_ch];
curNode->count++;
}
/**
* 在路径中该字符结点不存在,为该字符创建新的结点,
* 并继续向子节点遍历
*/
else
{
TrieNode* newNode = new TrieNode(str_ch);
curNode->next[str_ch] = newNode;
curNode = curNode->next[str_ch];
isUpdate = true; // 更新标志位置为true
}
}
/* 单词插入完成后,该结点的完整标志位置为true */
curNode->isWord = true;
/* 调用插入更新函数进行更新 */
if (isUpdate)
{
updateVec(curNode, str);
}
}
插入更新函数
void updateVec(TrieNode* curNode, string str)
{
/* 由后向前遍历,向根回溯并更新 */
int k = str.size();
auto it = str.rbegin();
while (it != str.rend())
{
char str_ch = *it;
TrieNode* node = curNode;
if (node != pRoot)
{
/* 每遍历到一个结点,更新其priString */
node->priString.push_back(str);
}
else
{
/* 注意根节点不更新priString */
break;
}
++it;
curNode = getchNode(str, --k);
}
}
删除主函数
bool remove(string str)
{
/* 通过search_Str查询函数判断Tire树中是否存在str 不存在返回false */
if (str.length() == 0 || !search_Str(str))
{
return false;
}
/* 调用删除更新函数 */
delPriWord(str);
······
}
删除更新函数
void delPriWord(string str)
{
/* 由后向前遍历,向根回溯并更新 */
int k = str.size();
auto it = str.rbegin();
while (it != str.rend())
{
char str_ch = *it;
TrieNode* node = getchNode(str, k--);
if (node != pRoot)
{
/* 遍历priString删除指定的元素 */
auto it = node->priString.begin();
while (it != node->priString.end())
{
if (*it == str)
{
/* 删除指定元素后,直接退出循环,继续向上回溯 */
node->priString.erase(it);
break;
}
++it;
}
}
else
{
/* 遍历到根节点,不作操作直接结束函数 */
break;
}
++it;
}
}
实现非遍历前缀模式匹配
void printPriWord(string str)
{
vector<string> res;
TrieNode* curNode = pRoot;
/**
* 遍历到前缀串的最后一个字符,因为最后一个字符中就存储
* 着该前缀的所有单词
*/
for (char str_ch : str)
{
if (curNode != nullptr)
{
curNode = curNode->next[str_ch];
}
}
if (curNode != nullptr)
{
/* 输出符合该前缀的所有单词 */
res = curNode->priString;
for (string val : res)
{
cout << val << endl;
}
cout << endl;
}
}
坑爹的内存泄露检查之路
由于代码量大,因此内存泄露的原因很难排查,最终还是成功解决了,就是因为我们之前在下图的箭头所指的区域使用的是free而非delete,但是free在我们之前的博文的Tire树结构中是适用的,因为创建出来的对象中所有资源都被正确的释放了;但是本文我们修改了Trie树的结构,增加了vector priString; 成员,即存在对象成员,我们必须使用delete进行释放,free来处理动态内存的时候,仅仅是释放了这个对象所占的内存,而不会调用这个对象的析构函数;使用delete就可以既释放对象的内存的同时,调用这个对象的析构函数。
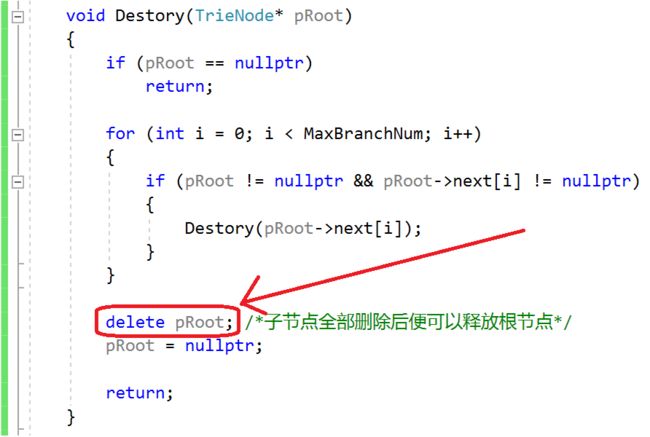
虽然问题很小,但是自己还是从这次调试中学到了很多知识,比较好的博文记录下来:
《VS检测内存泄漏,定位泄漏代码位置方法》
功能测试 - 《哈利波特》文章单词匹配
具体请参考我的另一篇博文
《基于Tire树(字典树)与倒排索引实现文件词频统计工具》
