深入浅出Python机器学习5——朴素贝叶斯
| 朴素贝叶斯基本概念/td> |
- 贝叶斯定理
请看后续概率论篇
- 朴素贝叶斯的简单应用
在过去7天,有4天没有下雨(用0表示),三天下雨(用1表示)。这7天里气象的情况如下表:
| 刮北风 | 闷热 | 多云 | 天气预报有雨 | |
|---|---|---|---|---|
| 第1天 | 否 | 是 | 否 | 是 |
| 第2天 | 是 | 是 | 是 | 否 |
| 第3天 | 否 | 是 | 是 | 否 |
| 第4天 | 否 | 否 | 否 | 是 |
| 第5天 | 否 | 是 | 是 | 否 |
| 第6天 | 否 | 是 | 否 | 是 |
| 第7天 | 是 | 否 | 否 | 是 |
用0表示否,1表示是。可得数组
X = [0, 1, 0, 1],[1, 1, 1, 0],[0, 1, 1, 0],[0, 0, 0, 1],[0, 1, 1, 0],[0, 1, 0, 1],[1, 0, 0, 1]。
程序中看一下数据关系:
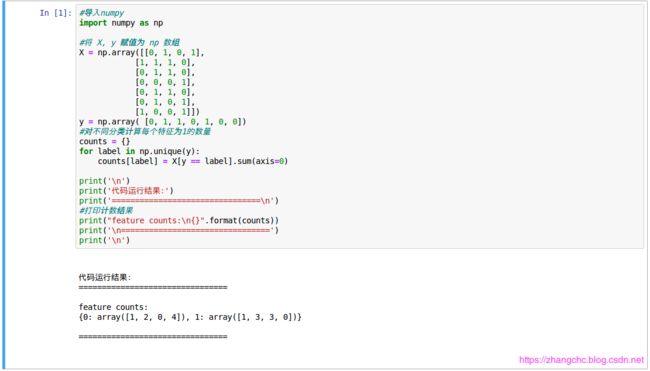
从结果看出,当没有下雨(y=0)时,1天刮了北风,2天闷热,0天多云,4天播报有雨。当下雨(y=1)时,1天刮了北风,3天闷热,3天多云,0天播报有雨。
那么对于朴素贝叶斯来说,它会根据上述的计算来进行推理。会认为,如果某一天天气预报没有播报有雨,但是出现了多云,它会倾向于把这一天放到"下雨"这类中。

如果另一天刮北风,闷热,少云,同时天气预报说有雨,这个时候天气预报会说没有雨。
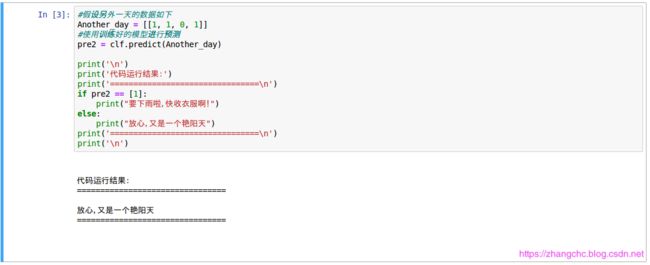
接下来,我们用predict_proba方法来测试一下下一天预测的准确率,
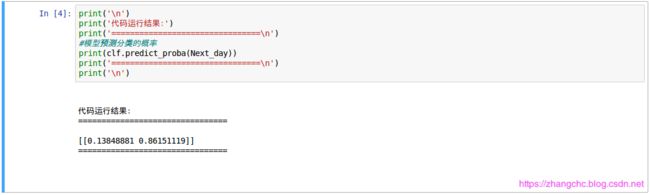
看到,有雨的概率大约时86.2%,没有雨的概率大约是13.8%,看起来还是不错的。
我们继续用predict_proba方法来测试一下另一天预测的准确率。

另一天没雨的概率是92.3%,有雨概率是7.7%,预测还是很不错。
注意:在scikit-learn官网文档中提出,虽然朴素贝叶斯是相当好的分类器,但对于预测具体的数值并不是很擅长,因此predict_proba给出的预测概率,大家也不要太当真。
| 朴素贝叶斯算法的不同方法 |
- 伯努利朴素贝叶斯
伯努利贝叶斯算法比较适合于分布服从伯努利分布的数据集,也称 “ 0-1分布 ” 或 “ 二项分布 ”。也就是数据集的每个特征只有 0 和 1 两个数值。

可以看到,在上图中我们用make_blobs 来生成手工生成的相对复杂数据集时,为了加大难度,我们令样本数量为500,而分类的数量为5(centers=5)个,伯努利贝叶斯的得分很糟糕,大概只有一半正确分类。
接下来看看伯努利贝叶斯的工作过程。

可以看出,伯努利朴素贝叶斯分类过程十分简单,分别在横轴和纵轴为 0 处画了两条直线,进一步用这两条直线生成 4 个象限对数据进行分类。这是因为我们使用了伯努利朴素贝叶斯的默认参数binarize=0,所以模型对于数据的判断时,如果特征 1 大于或等于 0,且特征 2 大于或等于 0,则将数据归为一类;如果特征 1 小于 0 且特征 2 小于 0,则归为另一类;而其余的数据归为第三类。
- 高斯朴素贝叶斯
高斯朴素贝叶斯,就是假设样本的特征符合高斯分布,或者说符合正态分布时所用的算法。接下来用高斯分布多上面的产生的数据进行拟合。

可以看出高斯朴素贝叶斯方法建立的模型得分要好了很多,准确率达到了96.8%,这说明我们生成的手工数据集的特征基本符合正态分布。
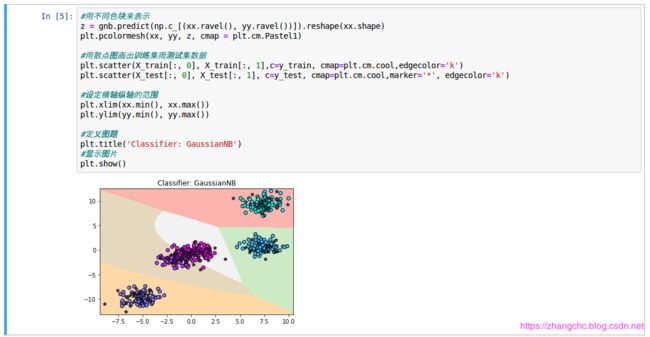
可以看出高斯朴素贝叶斯的分类边界要比伯努利朴素贝叶斯分类边界复杂的多,基本上将数据正确分类。
- 多项式朴素贝叶斯
多项式朴素贝叶斯主要应用于拟合多项式分布的数据集。先看看用上述数据集对多项式朴素贝叶斯的实验效果。

这里我们对X的值进行了一下处理使之为非负数据,否则程序会报错。
从结果可以看出,得分很糟糕。进一步看看分类过程。

看出比伯努利朴素贝叶斯还要差一些,说明不适合这个数据集。
这是因为多项式朴素贝叶斯只适合用来对非负离散数值特征进行分类,典型的例子就是对转化为向量后的文本数据进行分类。
| 朴素贝叶斯实战——判断肿瘤是良性还是恶性 |
- 对数据集进行分析
本次用的威斯康星乳腺肿瘤数据集包括569个病例的数据样本,每个样本具有30个特征值,而样本共分为两类:分别是恶性(Malignant)和良性(Benign)。

我们看到,这个数据集包含的信息有特征数据data、分类值target、分类名称target_names、数据描述DESCR和特征名称feature_names。
查看分类名称和特征名称。
- 使用高斯朴素贝叶斯进行建模
直觉判断这个数据集不是二项式分布,也不是多项式分布,我们用高斯朴素贝叶斯来建模。
首先我们要拆分数据集。

可以看出训练集中有 426 个样本,而测试集中有 143 个样本,特征数量均为 30 个。
用高斯朴素贝叶斯对训练数据集进行拟合,

可以看出,测试集和训练集得分都非常不错,均在95%左右。
接下来我们对其中一个样本(例如第312个)让模型测试一下。

可以看到,分类和正确的结果完全一致,都是分类1,也就是说,这个肿瘤是一个良性的肿瘤。
- 高斯朴素贝叶斯的学习曲线
在机器学习中,有一个概念成为学习曲线(learning curve),指的是随着数据集样本数量的增加,模型的得分变化情况。
看看高斯朴素贝叶斯在威斯康星乳腺肿瘤数据集中的学习曲线。

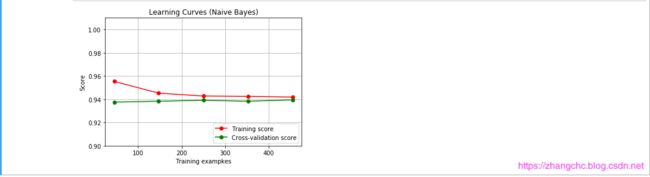
从图中我们发现,在训练数据集中,随着样本量的增加,模型的得分是逐渐降低的。这是因为随着样本数量增加,模型要拟合的数据越来越多,难度也越来越大,而模型的交叉验证得分的变化相对没有那么明显,从10个样本左右一直到500为止,分数一直在0.94左右浮动。这说明高斯朴素贝叶斯在预测方面,对样本数量的要求并没有那么苛刻。所以当样本数量比较少的话,可以考虑使用朴素贝叶斯算法来进行建模。
