2017-2018_2机器学习期末考点总结
1 概述
交叉验证的使用：模型评价、超参数（阈值）优选，保证数据集同分布留一法交叉验证——MAE平均绝对误差 评价
MAE（2 P68）
实值函数回归
2 KNN模型
KNNStep1 预处理
x估计=x-μ/σ
并且记录{μ(k),σ(k),k=1,2,3,4}
平均错误率、标准差
Step2 选K值 KNN中的K
m-fold（v） 2 p21
错误率最小的，作为最终的K，对样本集进行预测，K不能为偶数
m次，取n-1份作为训练集，1作为验证集合，得到(Acc(k),K)
Step3 决策
K近邻回归，2类别分类K为奇数，防止相等无法判断
p44 混淆矩阵
自然状态*预测输出（TP、FN、FP、TN）
p46 评价指标要记
总体正确率、总体错误率、查准率Precision、查全率Recall/灵敏度Sensiticity、特异度（真阴性率）、漏报率（假阴性率）、虚警率（假阳性率）、Fβ-Score（查准率和查全率的调和平均）F=2Precision·Recal /（Precision+Recall）
马修相关系数、Kappa系数
宏平均：先带入xx率公式计算，再求平均值
微平均：先求平均值，再带入xx率公式计算
3 基于树的模型
决策树主要是cartcart tree
不纯性度量：
-分类目标：Gini指标
-连续目标：最小平方残差、最小绝对残差
分类：叶子节点的输出怎么确定？ ①方差最小②基尼指数
最小二乘回归树：最优切分变量和切分点
选择(j,s)使得，特征j上的一点s，使得两边的 方差和相加最小。即寻找一个划分点，使两边的集合最紧致
得到两个划分区域后，确定相应输出值——相应区域内每个点的均值
迭代后，划分出M个区域，生成决策树
递归二叉分类树：基于基尼指数（最小）进行特征选择，最优二值切分点
对数据集D中输入的向量x的每个特征a遍历，得到使 基尼指数最小的切分点，最终的到(j,s)。
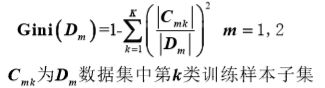
确定划分区域，将训练集D1,D2按照特征分配到两个子节点中
迭代后，划分为M个区域，生成决策树
剪枝不考
4 贝叶斯分类
模型学习 （C类） 4.1 p21朴素贝叶斯（高斯分布） 4.2 p66
宁愿误报也不能漏减
1).贝叶斯决策规则两个
最小错误率的贝叶斯分类 4.1 p20
最大似然作为正确的Acc，Err=1-Acc
最小风险的贝叶斯分类4.1 p31
加权，对不同的风险加上惩罚系数
2).两步贝叶斯决策过程
① 利用有限规模训练样本 估计先验概率和条件先验概率。
② 利用估计的hat P(ωi)、hat P(x|ωi)设计贝叶斯分类器，对未知样本x进行判决
即：先训练再验证
3).很重要！必须会！ 4.2 p12
一元和多元 正态分布概率密度函数，表达式
多元变量的参数的最大似然估计结果
特征相互独立，协方差矩阵为对角矩阵，且=0
4).高斯朴素贝叶斯分类
高斯分布+朴素贝叶斯
5).朴素贝叶斯，离散什么的
朴素贝叶斯表示，假定条件之间不相关，相互独立
LAPLACE 平滑 4.2 p58
上面+1，下面+选项个数
高斯混合模型有2个地方！
贝叶斯决策很多地方都用到了！
5 非监督式机器学习-聚类
p38 高斯混合模型 =高斯(正态)分布+极大似然估计高斯分布，αi（第i各高斯分布的先验概率），μi，Σ，3个参数求偏导得极大值
密度直达，密度可达，密度相连
样本集D=核心对象+边界对象+噪声点
分类、聚类、回归
聚类
高斯混合聚类 5.监督机机器学习 p40
基于最大似然估计，使得2个似然值均达到最大 p43
EM估计 p44
预测（缺失数据的最大似然估计）→配合更新计算当前概率→预测
共预测E次，更新M次
DBSCAN 密度直达、密度可达、密度相连 p59
层次聚类：合并式聚类、分裂式聚类 p76
6 主成分分析及应用
PCA：通过正交变换A，使得原始特征向量变为新特征向量，即主成分，且它们之间互不相关第二主成分对第一主成分剩余的部分有最大的解释能力 （方差最大），以此类推
A=[a1,...,ap]，其中
考虑新特征，并且计算各样本关于新特征的方差
Step1.确定a1
考虑新特征，并且计算各样本关于新特征的方差
。构造Lagrang目标函数
，关于a1求偏导数=0
，因为方差最大在极值点。a1为协方差矩阵Σ的本征值v对应的本征列向量。最后求得，v为Σ最大本征值λ1
（为了区分矩阵和协方差矩阵的特征值，矩阵的为特征值，协方差矩阵的为本征值）
Step2.确定a2
特征1和特征2不相关，协方差=0，并且方差最大
，多了一个条件因为Cov=0，构造Lagrange目标函数
，关于a2求偏导=0，得v2为Σ的本征列向量a2对应的本征值
Step3.确定其他ai及正交变换矩阵A
总结：求方差，扔进Lagrang求导，最终Lagrang乘子就是本征值。不知道为什么构造Lagrang函数。
例如三维投影到二维平面，使得所有点到平面的方差最小。
7 最小二乘线性回归及带有正则项的变种
最小二乘线性回归：一元线性回归，多元线性回归线性回归就是把点拟合成一条直线，各训练样本预测残差总体平方和最小（每个点到直线的距离的平方最小）
有3个主要参数，ω，b，ε，（y=f(x)+ε = ωx+b+ε）
因此多元中ε有n个，为了方便计算记hat ω =[ω b]T （hat是在ω上加一个帽子，表示估计值）
因为矩阵不一定可逆，因此要用伪逆计算
引入正则项：多元的参数预测值的收缩
引入关于估计系数的惩罚项（正则项）， 压缩系数估计值，将估计系数 向零的方向压缩
两种正则项的表达式和代表的意义：岭回归、LASSO回归
岭回归
由于最小二乘估计结果不稳定，数据集较小的变化可能会导致估计结果较大的差异。因此引入关于预测变量系数取值的惩罚项，确保目标函数是二次函数，防止过拟合。（惩罚项就是使得ω不能无限制的变化，限制范围）
注意：岭回归之前需要对训练样本输入、输出去中心化。甚至对预测变量进行尺度规范化（使得所有变量在相近的区间内波动）
不适合特征维度过高的情况。
LASSO回归
好像就是惩罚项没有平方了
LASSO法可以得到关于ω=[ω1,...,ωp]T 的稀疏向量
第一类 子集选择法
从p个预测变量中，挑选与响应变量y相关的变量，形成子集；对缩减后的变量子集应用最小二乘法。
第二类 压缩估计
基于全部预测变量，拟合模型。 采用不同的系数缩减法(即：正则法)，将估计系数向零的方向压缩。可将压缩估计法用于变量的选择。
首先借助降维，将p维预测变量，投影至M维子空间； 然后以投影后的M(M