主席树详解——从入门到放弃

要想学主席树，首先要搞懂可持久化线段树，因为主席树运用到了它的思想。

主席树的模板题是：静态查询区间第k小

那么主席树的做法就是，先把全部数字离散化，然后以每一个前缀建一棵权值线段树，显然，如果直接建，那么空间上是不允许的，但是我们发现，每两个相邻的前缀中，只有一个数的差别，所以，他们公共部分是很多的，于是，我们就可以用到可持久化线段树了！

首先，要明确一下，主席树上每个节点的值的定义（我们设这个节点的管理范围为l~r，并且现在已经将这个数列离散化了）：表示在当前前缀中，有多少个数的值在l~r中。

确定主席树的定义十分重要！网上有很多讲的不清楚的，搞得我懵逼了很久……

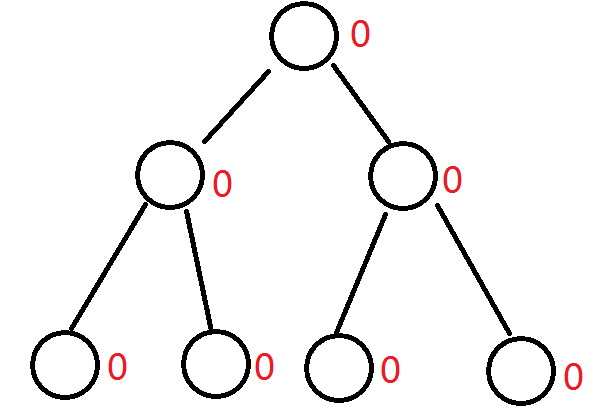
比如有下面这个数列{9,3,11,6}，离散化后就是{3,1,4,2}，那么我们要以每一个前缀建一棵线段树，首先，先建一棵空的线段树，表示当前什么数都没有，然后，我们把数列里的数一个一个加进去就好了，就像这样（红色数字表示每个节点的值，意义如上所述）：

那么首先加入第一个数——3，这棵树就会变成（节点里面是这个节点的管理范围，方便理解）：

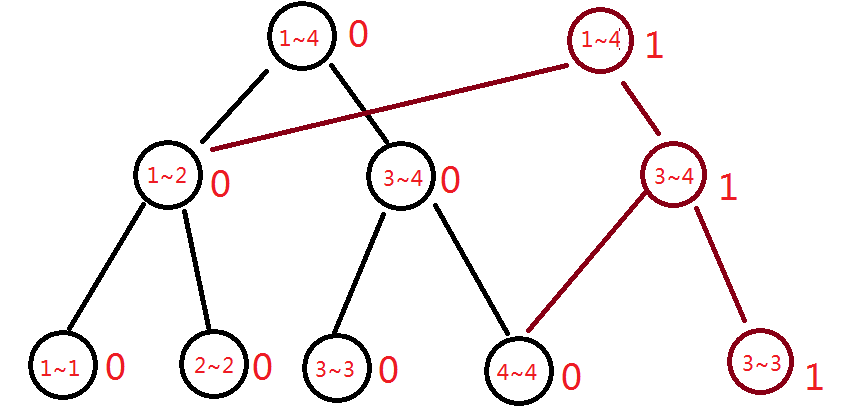
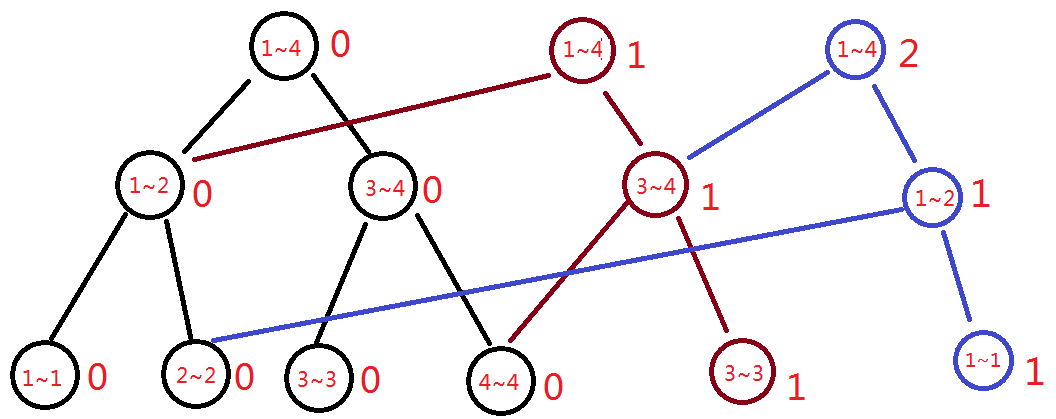
再加一个数——1，注意要在上一个前缀的基础上加（自己yy一下就知道什么意思了）：

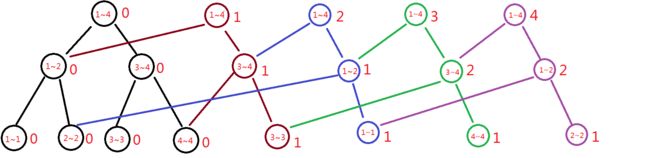
以此类推即可。。。最后得到的图是这个样子的（我画这个图是为了让大家后面可以看着这个图更好理解主席树，所以现在可以先不看...）：

好的，主席树就这样造出来了！那接下来就是查询，为了更好理解，我们先从简单的开始，假如要查询1~3范围中的第k小的数，假设k=2，那么可以直接从1~3这个前缀的根开始找， 也就是绿色的那个根，那么怎么找呢，因为可以保证，左边的数都比右边的数要小，所以我们发现，现在要找的是第2小，但是左儿子的值只有1，说明在1~3这个前缀里，在1~2范围内的只有1个数，那么第2小一定在右儿子里，于是我们往右儿子那里走一步，但是如果往右儿子那里走，k就要减去左儿子的值（蒟蒻语文不好。。实在想不到要怎么解释，自已意会一下吧，不难理解。。），然后因为k减了1，所以我们现在要找的就是第1小，然后发现当前节点的左儿子的值为1，k<=1，所以第k小一定在左儿子里，于是就走过去，然后发现这是个叶子节点，他管理的范围是3~3，说明这个第2小的数离散化之后的数是3，那么我们输出这个数原来是多少就好了，也就是9。

好的我们解决了在某个前缀中如何查找第k小，那么，现在要解决的问题是，查询区间第k小。

可能有人就会想到，你用前缀和来维护这个东西，那么要求一个区间就可以直接用前缀和相减嘛！

没错！就是相减。比如现在要求区间l~r的第k小，那么我们可以用a来存1~r这个前缀和上的根，b存1~l-1，那么每一次向下查找左右儿子的值的时候就先需要用a的左右儿子的值减去b的左右儿子的值，这样就可以去掉1~l-1中的数，只留下l~r区间的数，然后向上面一样查找即可。

代码如下（附有良心的注释）：

#include 
#include 
#include 
#include 
using namespace std;

int n,m,len=0,cnt=0;
int a[200010];
struct nod{int x,y;};
nod b[200010];
struct node{int l,r,zuo,you,c;};
node tree[5000010];
int gen[200010];
bool cmp(nod x,nod y){return x.x

待修主席树