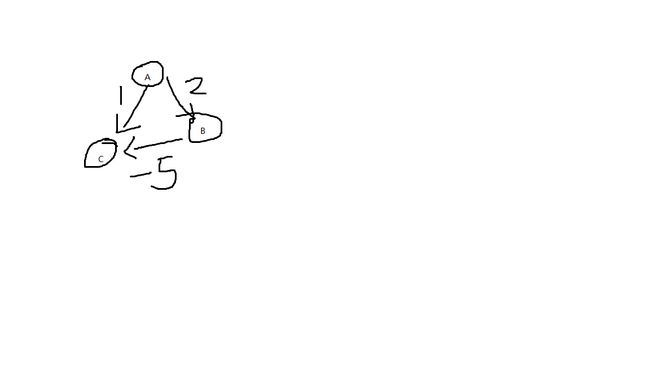最短路径 Floyd算法 Dijkstra算法 Bellman-Ford(贝尔曼)算法
相信大家应该对最短路径算法很感兴趣吧!不感兴趣也没关系,我们一起来看看下面的例子。最短路径应该是在众多算法中。最常用的一类算法。为什么这样说呢??
例如:
1.乘汽车旅行的人总希望找出到目的地的尽可能的短的行程。如果有一张地图并在图上标出每对十字路口之间的距离,如何找出这一最短行程?
2.某省自从实行了很多年的畅通工程计划后,终于修建了很多路。不过路多了也不好,每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。 现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。
那么如果想要求解这些问题,那么这里就会用到最短路径。
一:Floyd算法:
Floyd算法是一种求任意点到任意点的最短距离。可以求边权为负值,有向图、无向图等的最短路径。但是边权可以有负权值的边,但不能有包含负权值边组成的回路,不然算出来的就不是正确答案!!这个算法效率很低可以说是暴力。但是这种暴力是带着动态规划的暴力!!
那么为什么边权可以为负值,但是却不能有边权和为负值的回路呢??这是一个值得深思的问题。
问得好,这个问题是一个好问题。但是呢?我先把问题放在这!看过代码后我在给大家一组数据就可知道!!!
/*
floyd算法
*/
#include 模拟完后,我就要告诉你这个算法的特点是什么和该注意什么?这个算法的时间复查度是o(n^3) 是很大的稍微不注意就会超时。当然除了水题。。。它的目的是算任意节点到任意节点的距离,上面也提到过了。
这里最需要注意的就是为什么这个算法能求出含有负节点却不能算出含有负回路的图??只要是含有负回路,那么正确结果就是 负无穷。之所以能求含有负节点主要是因为 mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]); 的关系。其实不论是否为正数或者为负数。都是有大小的。让每步都最小,那么结果就最小。
二.Dijkstra算法
Dijkstra算法也是算最短路径的。它是只能算单源最短路径。当然你也可以把模板改了。把所有节点都遍历一遍也就成了算多源的模板。Dijkstra算法的主导思想是首先储存起点(你指定的点)到任意节点的距离,然后在这些距离中找一个最小值。毕竟你是求最短路径,肯定就是找最小的了。但是这种实现是根据动态规划实现。然后把你找到的点加入到起点中,我们这里的加入用的是标记。然后更新所有节点到起点的距离。然后重复就可以算出答案。
下面来看代码:
//Dijkstra算法
#includeint to=-1;
int d=Inf;
for(int j=1;j<=n;j++){
if(!vis[j]&&d>dis[j]){//如果j节点还没加入其实节点,并且1节点及加入1节点的节点到j节点有距离
d=dis[j];
to=j;
}
}
vis[to]=1;
for(int j=1;j<=n;j++){
if(!vis[j]&&dis[j]>dis[to]+mp[to][j]){
dis[j]=dis[to]+mp[to][j];//更新1节点到任意节点的距离。
}
}
}
}
int main(){
while(~scanf("%d%d",&n,&m)){
for(int i=1;i<=n;i++){//初始化默认距离表示i节点到j节点的距离。节点相同距离为0
for(int j=1;j<=n;j++){
if(i!=j){
mp[i][j]=Inf;
}else{
mp[i][j]=0;
}
}
}
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);//输入实际a点到b点的距离
mp[a][b]=c;
// mp[b][a]=c;//写上这个就是无向图
}
dij(1);//这里的1(数字1)表示我要求1这个节点到所有节点的最短距离!!!
for(int i=2;i<=n;i++){
printf("-->i=%d dis[%d]=%d\n\n",i,i,dis[i]);//dis中储存的表示1节点到任意节点的距离,当i=2时表示1节点到2节点的距离
}
}
return 0;
}
这里对于Dijkstra算法有需要注意的地方,那就是Dijkstra算法不能算含有负节点的图。当然更不可能算含有负节点回路的图。为什么呢??
我们这里就拿有向图来解答。看图片输入测试数据
3 3
1 3 1
1 2 2
2 3 -5
运行出来A-->B=2 A-->C=1肯定这样就错了应该是A-->B=2 A-->C=-3才对。
这也跟代码有关系因为这个代码的思想是贪心。局部贪心。所以会造成这样的结果。
三.Bellman-Ford算法
那么算单源最短路径Dijkstra算法不能算含有负值节点的并且也不能算含有负节点回路的。那么是否有其他算法呢??答案是有的,那就是Bellman-Ford算法,
#include//思考这里为什么是n-1次循环。
for(int j=1;j<=2*m;j++){
if(dis[tu[j].u]+tu[j].w//松弛操作。
}
}
}
for(int i=1;i<=2*m;i++){
if(dis[tu[i].u]+tu[i].w//判断是否还能松弛,如果能就含有负值回路。
return -1;
}
return 1;
}
int main(){
while(~scanf("%d%d",&n,&m)){
for(int i=1;i<2*m;i+=2){
int a,b,c;
scanf("%d%d%d",&tu[i].u,&tu[i].v,&tu[i].w);
tu[i+1].u=tu[i].v;
tu[i+1].v=tu[i].u;
tu[i+1].w=tu[i].w;
}
int x= bellman_floyd(1);
if(x==-1){
printf("no\n");
}else{
for(int i=1;i<=n;i++){
printf("dis[%d]=%d\n",i,dis[i]);
}
}
}
return 0;
} 为什么是n-1次松弛操作。
考虑:为什么要循环n-1次?
答:因为最短路径肯定是个简单路径,不可能包含回路的,
如果包含回路,且回路的权值和为正的,那么去掉这个回路,可以得到更短的路径
如果回路的权值是负的,那么肯定没有解了
图有n个点,又不能有回路
所以最短路径最多n-1边
又因为每次循环,至少relax一边
所以最多n-1次就行了
我们来举个实例。
6 5
5 6 1
4 5 2
3 4 3
2 3 4
1 2 5
就是这组测试数据。这是最坏的一种情况了。
那么为什么不能有负值环路这是另外一组测试数据。
6 6
1 2 1
2 3 -1
3 4 -1
4 5 -1
5 2 -1
5 6 1
这组数据就能很好的说明。
总结:Floyd算法能很好的解决稠密图(V大,V代表节点数)。而Dijkstra算法却能很好的解决稀疏图(E小,E代表边权数)。而SPFA也能很好解决稀疏图。(后面我会写的)
好了就说到这里了,如果有不足的地方请指正!!!谢谢!!