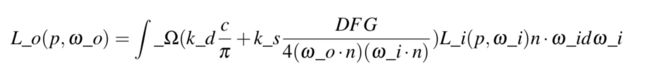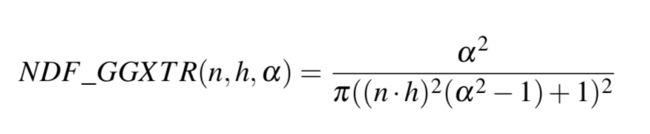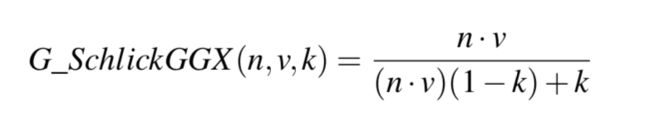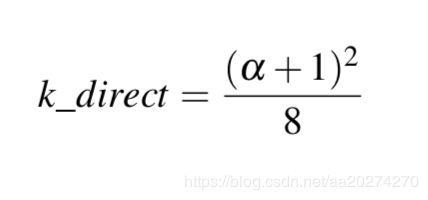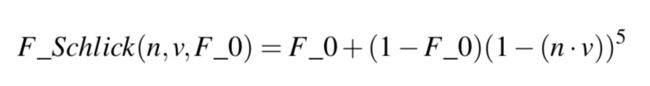LearnOpenGL 总结记录 PBR

Shader Code

vs:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoords;
layout (location = 2) in vec3 aNormal;

out vec2 TexCoords;
out vec3 WorldPos;
out vec3 Normal;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
    TexCoords = aTexCoords;
    WorldPos = vec3(model * vec4(aPos, 1.0));
    Normal = mat3(model) * aNormal;   

    gl_Position =  projection * view * vec4(WorldPos, 1.0);
}

 

fs:

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;
// ----------------------------------------------------------------------------
// Easy trick to get tangent-normals to world-space to keep PBR code simplified.
// Don't worry if you don't get what's going on; you generally want to do normal 
// mapping the usual way for performance anways; I do plan make a note of this 
// technique somewhere later in the normal mapping tutorial.
vec3 getNormalFromMap()
{
    vec3 tangentNormal = texture(normalMap, TexCoords).xyz * 2.0 - 1.0;

    vec3 Q1  = dFdx(WorldPos);
    vec3 Q2  = dFdy(WorldPos);
    vec2 st1 = dFdx(TexCoords);
    vec2 st2 = dFdy(TexCoords);

    vec3 N   = normalize(Normal);
    vec3 T  = normalize(Q1*st2.t - Q2*st1.t);
    vec3 B  = -normalize(cross(N, T));
    mat3 TBN = mat3(T, B, N);

    return normalize(TBN * tangentNormal);
}
// ----------------------------------------------------------------------------
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a = roughness*roughness;
    float a2 = a*a;
    float NdotH = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;

    return nom / denom;
}
// ----------------------------------------------------------------------------
float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}
// ----------------------------------------------------------------------------
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}
// ----------------------------------------------------------------------------
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
// ----------------------------------------------------------------------------
void main()
{		
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, vec3(2.2));
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;

    vec3 N = getNormalFromMap();
    vec3 V = normalize(camPos - WorldPos);

    // calculate reflectance at normal incidence; if dia-electric (like plastic) use F0 
    // of 0.04 and if it's a metal, use the albedo color as F0 (metallic workflow)    
    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance = lightColors[i] * attenuation;

        // Cook-Torrance BRDF
        float NDF = DistributionGGX(N, H, roughness);   
        float G   = GeometrySmith(N, V, L, roughness);      
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);
           
        vec3 nominator    = NDF * G * F; 
        float denominator = 4 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; // 0.001 to prevent divide by zero.
        vec3 specular = nominator / denominator;
        
        // kS is equal to Fresnel
        vec3 kS = F;
        // for energy conservation, the diffuse and specular light can't
        // be above 1.0 (unless the surface emits light); to preserve this
        // relationship the diffuse component (kD) should equal 1.0 - kS.
        vec3 kD = vec3(1.0) - kS;
        // multiply kD by the inverse metalness such that only non-metals 
        // have diffuse lighting, or a linear blend if partly metal (pure metals
        // have no diffuse light).
        kD *= 1.0 - metallic;	  

        // scale light by NdotL
        float NdotL = max(dot(N, L), 0.0);        

        // add to outgoing radiance Lo
        Lo += (kD * albedo / PI + specular) * radiance * NdotL;  // note that we already multiplied the BRDF by the Fresnel (kS) so we won't multiply by kS again
    }   
    
    // ambient lighting (note that the next IBL tutorial will replace 
    // this ambient lighting with environment lighting).
    vec3 ambient = vec3(0.03) * albedo * ao;
    
    vec3 color = ambient + Lo;

    // HDR tonemapping
    color = color / (color + vec3(1.0));
    // gamma correct
    color = pow(color, vec3(1.0/2.2)); 

    FragColor = vec4(color, 1.0);
}

解析：

1. 上面的pbr 只考虑到 直接光照，主要使用到的公式就是:

With every component of the Cook-Torrance BRDF described we can include the physically based BRDF into the now final reflectance equation:

This equation now completely describes a physically based render model that is generally recognized as what we commonly understand as physically based rendering or PBR.

 

a.  Normal distribution function (D项, DistributionGGX函数)

The normal distribution function D or the specular distribution statistically approximates the ratio of microfacets aligned to some (halfway) vector h. There are a multitude of NDFs defined that statistically approximate the general alignment of the microfacets given some roughness parameter and the one we’ll be using is known as the Trowbridge-Reitz GGX:

Here h is the halfway vector to measure against the surface’s microfacets, with a being a measure of the surface’s roughness. 

 

b. Geometry function (G项, GeometrySmith 函数)

The geometry function statistically approximates the ratio of microfacets that overshadow each other causing light rays to lose their energy in the process.

Similar to the NDF, the Geometry function takes a material’s roughness parameter as input with rougher surfaces having a higher probability of overshadowing microfacets. The geometry function we will use is a combination of the GGX and Schlick-Beckmann approximation known as Schlick-GGX:

Here k is a remapping of α based on whether we’re using the geometry function for either direct lighting or IBL lighting:

Note that the value of α might differ based on how your engine translates roughness to α. In the following tutorials we’ll extensively discuss how and where this remapping becomes relevant.

To effectively approximate the geometry we need to take account of both the view direction (geometry obstruction) and the light direction vector (geometry shadowing). We can take both into account usingSmith’s method:

 

c. Fresnel equation (F项，fresnelSchlick 函数)

The Fresnel equation (pronounced as Freh-nel) describes the ratio of light that gets reflected over the light that gets refracted, which varies over the angle we’re looking at a surface. The moment light hits a surface, based on the surface to view angle the Fresnel equation tells us the percentage of light that gets reflected. From this ratio of reflection and the energy conservation principle we can directly obtain the refracted portion of light from its remaining energy.

The Fresnel equation is a rather complex equation, but luckily the Fresnel equation can be approximated using the Fresnel-Schlick approximation:

 

2. 这里需要注意的是，公式中有一个积分，但是由于是点光源，所以点光源对P点的贡献只有一个方向，也就是如果只有一个点光源的话，P点积分半球所有方向，来求所有的入射光的话，得到的也只有wi方向的入射光。这里只是考虑到直接光照是点光源的特色情况。

Well, imagine we have a single point light (a light source that shines equally bright inalldirections)witharadiantfluxof(23.47, 21.31, 20.79)as translated to an RGB triplet.The radiant intensity of this light source equals its radiant flux at all outgoing direction rays. However, when shading a specific point p on a surface, of all possible incoming light directions over its hemisphere Ω only one incoming direction vector w_i directly comes from the point light source. As we only have a single light source in our scene, assumed to be at a single point in space, all other possible incoming light directions have zero radiance observed over the surface point p:

3. sRGB 和 tonemapping, gamma correct

(如何输入的Texture 是sRGB的话，那么就需要把sRGB转为RGB，也就是执行 

vec3 albedo = pow(texture(albedoMap, TexCoords).rgb, vec3(2.2));

在shader输出的时候，执行 tonemapping, gamma correct

)

Note that the albedo textures that come from artists are generally authored in sRGB space which is why we first convert them to linear space before using albedo in our lighting calculations. Based on the system artists use to generate ambient occlusion maps you might also have to convert these from sRGB to linear space as well. Metallic and roughness maps are almost always authored in linear space.

 

So far we’ve assumed all our calculations to be in linear color space and to account for this we need togamma correct at the end of the shader. Calculating lighting in linear space is incredibly important as PBR requires all inputs to be linear, not taking this into account will result in incorrect lighting. Additionally, we want light inputs to be close to their physical equivalents such that their radiance or color values can vary wildly over a high spectrum of values. As a result Lo can rapidly grow really high which then gets clamped between 0.0 and 1.0 due to the default low dynamic range (LDR) output. We fix this by taking Lo and tone or exposure map the high dynamic range (HDR) value correctly to LDR before gamma correction:

    // HDR tonemapping
    color = color / (color + vec3(1.0));
    // gamma correct
    color = pow(color, vec3(1.0/2.2)); 

Here we tone map the HDR color using the Reinhard operator, preserving the high dynamic range of possibly highly varying irradiance after which we gamma correct the color. We don’t have a separate framebuffer or post-processing stage so we can directly apply both the tone mapping step and gamma correction step directly at the end of the forward fragment shader.