滑块拼图(加强版的8数码)的规划处理
最近回顾了下BFS,DFS,以及八数码问题
周末的时候在家突然看到了角落里的滑块拼图,放了很久了。
玩滑块拼图,没有找到什么规律的话太难下手了。
这时,考虑用程序来处理下。
3*4 + 1的拼图,是8数码的升级版,8数码问题的资料还比较多,是一个非常经典的问题
https://blog.csdn.net/u012283461/article/details/79078653
https://www.jianshu.com/p/9c39e80cc877
常规的处理需要保存所有可能的状态,估算下状态总数为
13! = 6 227 020 800
数据量非常大,大概是6G大小
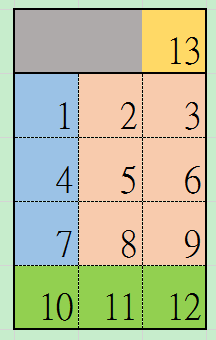
初始形态
模型图如下
这里,考虑分块处理,先拼好部分位置,如最下面的一行,
再处理剩余的部分,数据量下降后就可以类似8数码的解决方案去处理3*3 + 1的拼图了
这里探讨一下使用bfs方法找到最下面一行的处理方案
现在只关心4个小图片的存放位置,
//通过15*15*15*15的存储空间,可以保存4个块的所有排列组合方案(使用15*15*15*15还是有冗余空间的)
//pixrecords[15][15][15][15] = {0};
//record the 4 pix
//pixrecords[12][14][7][6]表示数字10在12位置,数字11在14位置,数字12在7位置,空白块在6位置
其他的处理就是常规的广度优先搜索了,使用一个队列去实现。
VC6中编译通过的code
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int width = 3;
int height = 5;
struct PNode{
char state[15];
char steps[32];
char pos[4];
// int pred;
PNode()
{
}
};
//record the 0,1,2,3 pix
//pixrecords[12][14][7][6]表示数字1在12位置,数字2在14位置,数字3在7位置,空白块在6位置
//通过15*15*15*15的存储空间,可以保存4个块的所有排列组合方案
char pixrecords[15][15][15][15] = {0};
//
//right left, up down
int directions[8] = {0, 1, 0, -1, -1, 0, 1, 0};
bool isMoveable(int x, int y, int d)
{
//d 1 2 3 4
x += directions[2*(d-1)];
y += directions[2*(d-1) + 1];
if (y >= 0 && y <= 2 && x >=1 && x <=4)
{
return true;
}
if (y == 2 && x == 0)
{
return true;
}
return false;
}
int move(char* data, char* positon, int d)
{
int x = positon[3] / 3;
int y = positon[3] % 3;
int x1 = x + directions[2*(d-1)];
int y1 = y + directions[2*(d-1) + 1];
// printf("The begin positions = %d %d %d %d, d=%d, x=%d,y=%d, x1=%d, y1=%d\n",
// positon[0],positon[1],positon[2],positon[3],d,x,y,x1,y1);
for (int i = 0; i < 3; i++)
{
if (positon[i] == width*x1 + y1)
{
positon[i] = width*x + y;
}
}
positon[3] = width*x1 + y1;
int p1 = positon[0];
int p2 = positon[1];
int p3 = positon[2];
int p4 = positon[3];
if (pixrecords[p1][p2][p3][p4] == 1)
{
printf("positions = %d %d %d %d\n", p1,p2,p3,p4);
return 0;
}
pixrecords[p1][p2][p3][p4] = 1;
printf("make 1, positions = %d %d %d %d\n", p1,p2,p3,p4);
int tmp = data[width*x + y];
data[width*x + y] = data[width*x1 + y1];
data[width*x1 + y1] = tmp;
return 1;
}
bool isOk(char* data)
{
if (data[12] == 10 && data[13] == 11 && data[14] == 12)
{
return true;
}
return false;
}
int getIndex(char* data, char value)
{
for (int i = 0; i < 15; i++)
{
if (data[i] == value)
{
return i;
}
}
return 0;
}
int main()
{
//这里我们只关心4个小块,他们的值分别设置为10,11,12,13(空白块)
char beginData[15] = {
0, 0, 9,
9, 9, 9,
13, 9, 9,
9, 10, 9,
12,11, 9};
char pixpositon[4];
//for example
// char pixpositon[4] = {5, 11, 7, 4};
// pixrecords[5][11][7][4] = 1;
pixpositon[0] = getIndex(beginData, 10);
pixpositon[1] = getIndex(beginData, 11);
pixpositon[2] = getIndex(beginData, 12);
pixpositon[3] = getIndex(beginData, 13);
pixrecords[pixpositon[0]][pixpositon[1]][pixpositon[2]][pixpositon[3]] = 1;
PNode start;
memcpy(start.state, beginData, 15);
memset(start.steps, 0, 32);
memcpy(start.pos, pixpositon, 4);
queue
plist.push(start);
int pcount = 0;
while (!plist.empty())
{
pcount++;
if (pcount % 100 == 0)
{
cout << "count = " << pcount << ", list len = " << plist.size() << endl;
}
PNode cur = plist.front();
plist.pop();
if (isOk(cur.state))
{
//cout << "the steps is; " << cur.steps << endl;
for (int i = 0; i < strlen(cur.steps); i++)
{
printf(" %d,", cur.steps[i]);
}
cout << endl;
//right left, up down
for (i = 0; i < strlen(cur.steps); i++)
{
if (cur.steps[i] == 1) printf(" right,");
if (cur.steps[i] == 2) printf(" left,");
if (cur.steps[i] == 3) printf(" up,");
if (cur.steps[i] == 4) printf(" down,");
}
cout << endl;
break;
}
for (int i = 1; i <= 4; i++)
{
if (isMoveable(cur.pos[3]/3, cur.pos[3]%3, i))
{
// cout << "in moveable " << endl;
PNode node;
memcpy(&node, &cur, sizeof(PNode));
if (move(node.state, node.pos, i) == 1)
{
int len = strlen(node.steps);
node.steps[len] = i;
plist.push(node);
// cout << "push " << endl;
}
}
}
}
cout << "end, count = "<< pcount << endl;
return 0;
}
执行结果
4, 1, 4, 2, 3, 3, 1, 1, 4, 4, 2, 3,
down, right, down, left, up, up, right, right, down, down, left, up,
可以继续使用这个方法来排3个小图片
up, left, up, right,
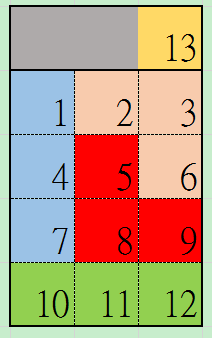
这样问题的规模越来越小了,再选择3个进行处理,下图红色部分
4, 4, 1, 3,
down, down, right, up,
就差不多还原好了,只差最后一击了