ML笔记:LDA(Fisher) 线性判别分析最全解读+python实战二分类代码+补充:矩阵求导可以参考!
| LDA(Fisher) 线性判别分析最全解读+python实战二分类代码! |
文章目录
- 一、主要思想!
- 二、具体流程!
- 三、补充二中的公式的证明!
- 四、目标函数的求解过程!
- 4.1、优化问题的转化
- 4.2、拉格朗日乘子法求解
- 五、拓展到多分类任务中
- 六、Fisher实战分析:二分类
- 6.1、数据生成
- 6.2、fisher算法
- 6.3、判断类别
- 6.4、绘图
- 6.5、运行结果
- 参考文章
- 补充:矩阵求导可以参考
一、主要思想!
线性判别分析(Linear Discriminant Analysis 简称LDA)是一种经典的线性学习方法,在二分类问题上因为最早由【Fisher,1936年】提出,所以也称为“Fisher 判别分析!”
Fisher(费歇)判别思想是投影,使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是:使每一类内的投影值所形成的类内离差尽可能小,而不同类间的投影值所形成的类间离差尽可能大。
| 图摘自周志华老师的《机器学习》一书 |
|---|
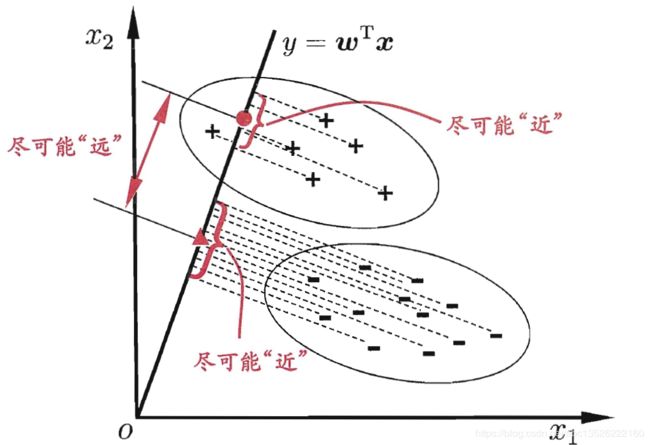
|
简单介绍:LDA的思想非常的朴素,给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能的远离;在对新鲜样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别,上图中给出了一个二维示意图。
我们寻找一个投影方向 w \boldsymbol w w,( w \boldsymbol w w的维度和每个样本维度相同!),投影之后的样本变为:
y i = w T x i , i = 1 , 2 , ⋯ , N (1-1) y_{i}=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}, \quad i=1,2, \cdots, N\tag{1-1} yi=wTxi,i=1,2,⋯,N(1-1)
二、具体流程!
为了找到最佳投影方向,需要计算出各类样本均值、样本类内离散度矩阵 S i \boldsymbol S_{i} Si 和样本总类内离散度矩阵 S w \boldsymbol S_{w} Sw、样本类间离散度矩阵 S b \boldsymbol S_{b} Sb,根据Fisher准则,找到最佳投影向量,将训练集内的所有样本进行投影,投影到一维Y空间,由于Y空间是一维的,则需要求出Y空间的划分边界点,找到边界点后,就可以对待测样本进行一维Y空间投影,判断它的投影点与分界点的关系,将其归类。具体方法如下:
1、计算各类样本均值向量 m i m_{i} mi, m i m_{i} mi是各个类的均值, N i N_{i} Ni是 w i w_{i} wi类的样本个数。
m i = 1 N i ∑ x j ∈ ω i x j i = 1 , 2 (2-1) m_{i}=\frac{1}{N_{i}} \sum_{\boldsymbol{x}_{j} \in \omega_{i}} \boldsymbol{x}_{j}\quad i=1,2\tag{2-1} mi=Ni1xj∈ωi∑xji=1,2(2-1)
2、计算样本类内离散度矩阵 S i \boldsymbol S_{i} Si 和总类内离散度矩阵 S w \boldsymbol S_{w} Sw
S i = ∑ x j ∈ w i ( x j − m i ) ( x j − m i ) T , i = 1 , 2 (2-2) \boldsymbol{S}_{i}=\sum_{\boldsymbol{x}_{j} \in w_{i}}\left(\boldsymbol{x}_{j}-\boldsymbol{m}_{i}\right)\left(\boldsymbol{x}_{j}-\boldsymbol{m}_{i}\right)^{\mathrm{T}}, \quad \boldsymbol{i}=1,2\tag{2-2} Si=xj∈wi∑(xj−mi)(xj−mi)T,i=1,2(2-2) S w = S 1 + S 2 (2-3) \boldsymbol{S}_{\mathrm{w}}=\boldsymbol{S}_{1}+\boldsymbol{S}_{2}\tag{2-3} Sw=S1+S2(2-3)
3、计算样本类间离散度矩阵 S b \boldsymbol S_{b} Sb。
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T (2-4) \boldsymbol{S}_{\mathrm{b}}=\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)^{\mathrm{T}}\tag{2-4} Sb=(m1−m2)(m1−m2)T(2-4)
4、求投影方向向量 W W W(维度和样本的维度相同)。我们希望投影后,在一维Y空间里各类样本尽可能分开,就是我们希望的两类样本均值之差 ( m ~ 1 − m ~ 2 ) \left(\tilde \boldsymbol{m}_{1}-\tilde \boldsymbol{m}_{2}\right) (m~1−m~2)越大越好,同时希望各类样本内部尽量密集,即是:希望类内离散度越小越好,因此,我们可以定义Fisher准则函数为:
J F ( w ) = w T S b w w T S w w (2-5) J_{F}(w)=\frac{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{b} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{w} \boldsymbol{w}}\tag{2-5} JF(w)=wTSwwwTSbw(2-5)
使得 J F ( w ) J_{F}(\boldsymbol{w}) JF(w) 取得最大值的 w \boldsymbol{w} w 为:
w = S w − 1 ( m 1 − m 2 ) (2-6) \boldsymbol{w}=\boldsymbol{S}_{w}^{-1}\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)\tag{2-6} w=Sw−1(m1−m2)(2-6)
5、将训练集内所有样本进行投影。
y = w T x (2-7) y=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}\tag{2-7} y=wTx(2-7)
6、计算在投影空间上的分割阈值 y 0 y_{0} y0。
在一维Y空间,各类样本均值 m ~ i \widetilde \boldsymbol{m}_{i} m i 为:
m ~ i = 1 N i ∑ y j ∈ w i y j = 1 N i ∑ x j ∈ w i w T x j = w T m i i = 1 , 2 (2-8) \tilde{m}_{i}=\frac{1}{N_{i}} \sum_{y_{j} \in w_{i}} y_{j}=\frac{1}{N_{i}} \sum_{\boldsymbol{x}_{j} \in w_{i}} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x_{j}}=\boldsymbol{\boldsymbol{w}}^{\mathrm{T}} \boldsymbol{m}_{\boldsymbol{i}} \quad i=1,2\tag{2-8} m~i=Ni1yj∈wi∑yj=Ni1xj∈wi∑wTxj=wTmii=1,2(2-8)
注意: 对于二类问题,此时类内离散度不再是一个矩阵,而是一个值。还有可以发现: S w \boldsymbol S_{w} Sw 和 S b \boldsymbol S_{b} Sb都是对称矩阵,故 S b = S b T , S w = S w T \boldsymbol{S}_{b}=\boldsymbol{S}_{b}^{T}, \boldsymbol{S}_{w}=\boldsymbol{S}_{w}^{T} Sb=SbT,Sw=SwT
样本类内离散度 s ~ i 2 \tilde{s}_{i}^{2} s~i2 和总类内离散度 s ~ w \tilde{s}_{w} s~w
s ~ i 2 = ∑ y ∈ w i ( y − m ~ i ) 2 i = 1 , 2 (2-9) \tilde{s}_{i}^{2}=\sum_{y \in w_{i}}\left(y-\widetilde{m}_{i}\right)^{2} \quad i=1,2\tag{2-9} s~i2=y∈wi∑(y−m i)2i=1,2(2-9)
s ~ w = s ~ 1 2 + s ~ 2 2 (2-10) \tilde{s}_{w}=\tilde{s}_{1}^{2}+\tilde{s}_{2}^{2}\tag{2-10} s~w=s~12+s~22(2-10)
而此时类间离散度就成为两类均值差的平方。
S ~ b 2 = ( m ~ 1 − m ~ 2 ) 2 (2-11) \widetilde{S}_{b}^{2}=\left(\tilde{m}_{1}-\tilde{m}_{2}\right)^{2}\tag{2-11} S b2=(m~1−m~2)2(2-11)
阈值 y 0 y_{0} y0的选择可以有不同的方案:
- 比较常用的一种是:
y 0 = N 1 m ~ 1 + N 2 m ~ 2 N 1 + N 2 (2-12) y_{0}=\frac{N_{1} \tilde{m}_{1}+N_{2} \tilde{m}_{2}}{N_{1}+N_{2}}\tag{2-12} y0=N1+N2N1m~1+N2m~2(2-12) - 另外一种是
y 0 = m ~ 1 + m ~ 2 2 + ln ( P ( ω 1 ) / P ( ω 2 ) ) N 1 + N 2 − 2 (2-13) y_{0}=\frac{\tilde{m}_{1}+\tilde{m}_{2}}{2}+\frac{\ln \left(P\left(\omega_{1}\right) / P\left(\omega_{2}\right)\right)}{N_{1}+N_{2}-2}\tag{2-13} y0=2m~1+m~2+N1+N2−2ln(P(ω1)/P(ω2))(2-13)
7、对于给定的测试样本 x \boldsymbol{x} x,计算出它在 w \boldsymbol w w 上的投影点 y y y。 y = w T x (2-14) y=\boldsymbol w^{\mathrm{T}} \boldsymbol{x}\tag{2-14} y=wTx(2-14)
8、根据决策规则分类!
{ y > y 0 ⇒ X ∈ ω 1 y < y 0 ⇒ X ∈ ω 2 (2-15) \left\{\begin{array}{l}{y>y_{0} \Rightarrow X \in \omega_{1}} \\ {y
三、补充二中的公式的证明!
刚才我们提到过,希望寻找的投影方向使投影以后两类尽可能的分开,而各类内部由尽可能聚集,这一目标函数可表示为如下的准则(Fisher准则函数): max J F ( w ) = S ~ b 2 S ~ w 2 = ( m ~ 1 − m ~ 2 ) 2 S ~ 1 2 + S ~ 2 2 (3-1) \max J_{\mathrm{F}}(w)=\frac{\widetilde{\mathrm{S}}_{\mathrm{b}}^{2}}{\widetilde{S}_{\mathrm{w}}^{2}}=\frac{\left(\tilde{m}_{1}-\tilde{m}_{2}\right)^{2}}{\widetilde{S}_{1}^{2}+\widetilde{S}_{2}^{2}}\tag{3-1} maxJF(w)=S w2S b2=S 12+S 22(m~1−m~2)2(3-1)
其中: S ~ b 2 = ( m ~ 1 − m ~ 2 ) 2 = ( w T m 1 − w T m 2 ) 2 = w T ( m 1 − m 2 ) ( m 1 − m 2 ) w = w T S b w (3-2) \begin{aligned} \widetilde{S}_{\mathrm{b}}^{2} &=\left(\tilde{m}_{1}-\tilde{m}_{2}\right)^{2} \\ &=\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{m}_{1}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{m}_{2}\right)^{2} \\ &=\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right) \boldsymbol{w} \\ &=\boldsymbol{w}^{\mathrm{T}} S_{\mathrm{b}} \boldsymbol{w} \end{aligned}\tag{3-2} S b2=(m~1−m~2)2=(wTm1−wTm2)2=wT(m1−m2)(m1−m2)w=wTSbw(3-2)
以及下面的公式:
S ~ w = S ~ 1 2 + S ~ 2 2 = ∑ x j ∈ w 1 ( w T x j − w T m 1 ) 2 + ∑ x j ∈ w 2 ( w T x j − w T m 2 ) 2 = ∑ x j ∈ w 1 w T ( x j − m 1 ) ( x j − m 1 ) T w + ∑ x j ∈ w 2 w T ( x j − m 2 ) ( x j − m 2 ) T w = w T S 1 w + w T S 2 w = w T S w w (3-3) \begin{aligned}\widetilde{S}_{w}&=\widetilde{S}_{1}^{2}+\widetilde{S}_{2}^{2} \\ & =\sum_{x_{j} \in w_{1}}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{j}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{m}_{1}\right)^{2}+\sum_{\boldsymbol{x}_{j} \in w_{2}}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{j}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{m}_{2}\right)^{2} \\&=\sum_{x_{j} \in w_{1}} \boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_{\boldsymbol{j}}-\boldsymbol{m}_{1}\right)\left(\boldsymbol{x}_{\boldsymbol{j}}-\boldsymbol{m}_{1}\right)^{\mathrm{T}} \boldsymbol{w}+\sum_{x_{j} \in w_{2}} \boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{x}_{j}-\boldsymbol{m}_{2}\right)\left(\boldsymbol{x}_{j}-\boldsymbol{m}_{2}\right)^{\mathrm{T}} \boldsymbol{w}\\&= {\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{1} \boldsymbol{w}+\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{2} \boldsymbol{w}} \\ &={\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{w} \boldsymbol{w}}\end{aligned}\tag{3-3} S w=S 12+S 22=xj∈w1∑(wTxj−wTm1)2+xj∈w2∑(wTxj−wTm2)2=xj∈w1∑wT(xj−m1)(xj−m1)Tw+xj∈w2∑wT(xj−m2)(xj−m2)Tw=wTS1w+wTS2w=wTSww(3-3)
因此,Fisher判别准则(目标函数)变为:这一表达式在数学物理中称为广义Rayleigh商(generalized Rayleigh quotient)
max w J F ( w ) = w T S b w w T S w w (4-1) \max _{w} J_{\mathrm{F}}(\boldsymbol{w})=\frac{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{\mathrm{b}} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{\mathrm{w}} \boldsymbol{w}}\tag{4-1} wmaxJF(w)=wTSwwwTSbw(4-1)
四、目标函数的求解过程!
4.1、优化问题的转化
我们的目标就是求得使(4-1)最大的投影方向 W W W, 由于对 W \boldsymbol{W} W的幅值调节并不会影响 W \boldsymbol{W} W的方向,即不会影响( J F ( w ) J_{\mathrm{F}}(\boldsymbol{w}) JF(w)),因此可以设定式(4-1)的分母为非0常数(设置为1),最大化分子部分,即把式(4-1)的优化问题转化为下面的(4-2):
max w T S b w s. t. w T S w w = c = 0̸ (4-2) \begin{array}{cl}{\max } & {\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{\mathrm{b}} \boldsymbol{w}} \\ {\text { s. t. }} & {\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{\mathrm{w}} \boldsymbol{w}=c =\not0}\end{array}\tag{4-2} max s. t. wTSbwwTSww=c=0(4-2)
4.2、拉格朗日乘子法求解
这是一个等式约束下的极值问题,可以通过引入拉格朗日(lagrange)乘子转化为以下拉个朗日函数的无约束极值问题:
L ( w , λ ) = w T S b w − λ ( w T S w w − c ) (4-3) L(w, \lambda)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{\mathrm{b}} \boldsymbol{w}-\lambda\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{S}_{w} \boldsymbol{w}-c\right)\tag{4-3} L(w,λ)=wTSbw−λ(wTSww−c)(4-3)
在式(4-3)的极值处,应该满足:
∂ L ( w , λ ) ∂ w = 0 (4-4) \frac{\partial L(\boldsymbol{w}, \lambda)}{\partial \boldsymbol{w}}=0\tag{4-4} ∂w∂L(w,λ)=0(4-4)
由此得到,极值解 w \boldsymbol{w} w,应该满足:
∂ L ( w , λ ) ∂ w = ∂ ( w T S b w ) ∂ w − λ ( w T S w w − c ) ∂ w = ( S b + S b T ) w − λ ( S w + S w T ) w (4-5) \begin{aligned}\frac{\partial L(\boldsymbol{w}, \lambda)}{\partial \boldsymbol{w}}&=\frac{\partial\left(\boldsymbol{w}^{T} \boldsymbol{S}_{b} \boldsymbol{w}\right)}{\partial \boldsymbol{w}}-\lambda \frac{\left(\boldsymbol{w}^{T} \boldsymbol{S}_{w} \boldsymbol{w}-c\right)}{\partial \boldsymbol{w}} \\ &=\left(\boldsymbol{S}_{b}+\boldsymbol{S}_{b}^{T}\right) \boldsymbol{w}-\lambda\left(\boldsymbol{S}_{w}+\boldsymbol{S}_{w}^{T}\right) \boldsymbol{w} \end{aligned}\tag{4-5} ∂w∂L(w,λ)=∂w∂(wTSbw)−λ∂w(wTSww−c)=(Sb+SbT)w−λ(Sw+SwT)w(4-5)
又 S b = S b T , S w = S w T \boldsymbol{S}_{b}=\boldsymbol{S}_{b}^{T}, \boldsymbol{S}_{w}=\boldsymbol{S}_{w}^{T} Sb=SbT,Sw=SwT,则 ∂ L ( w , λ ) ∂ w = = 2 S b w − 2 λ S w w (4-6) \begin{aligned}\frac{\partial L(\boldsymbol{w},\lambda)}{\partial \boldsymbol{w}}==2 \boldsymbol{S}_{b} \boldsymbol{w}-2 \lambda \boldsymbol{S}_{w} \boldsymbol{w}\end{aligned}\tag{4-6} ∂w∂L(w,λ)==2Sbw−2λSww(4-6)
注意:这里可以参考维基百科的矩阵演算:Scalar-by-matrix identities;这里求导用的公式: ∂ x T A x ∂ x = ( A + A T ) x \frac{\partial \mathbf{x}^{\mathbf{T}} \mathbf{A} \mathbf{x}}{\partial \mathbf{x}}=\left(\mathbf{A}+\mathbf{A}^{\mathbf{T}}\right) \mathbf{x} ∂x∂xTAx=(A+AT)x
令导函数等于0
S b w − λ S w w = 0 (4-7) \boldsymbol{S}_{b} \boldsymbol{w}- \lambda \boldsymbol{S}_{w} \boldsymbol{w}=0\tag{4-7} Sbw−λSww=0(4-7)
假定 S w S_{w} Sw是非奇异的(样本数大于维数时通常是非奇异的),可以得到 S w − 1 S b w = λ w (4-8) \boldsymbol{S}_{\mathrm{w}}^{-1} \boldsymbol{S}_{\mathrm{b}} \boldsymbol{w}=\lambda \boldsymbol{w}\tag{4-8} Sw−1Sbw=λw(4-8)
也就是说, w \boldsymbol{w} w是矩阵 S w − 1 S b \boldsymbol{S}_{\mathbf{w}}^{-1} \boldsymbol{S}_{\mathrm{b}} Sw−1Sb的本征向量。我们把式 (2-4) 的 S b \boldsymbol{S_{b}} Sb代入,式(4-8)变为:
λ w = S w − 1 ( m 1 − m 2 ) ( m 1 − m 2 ) T w (4-9) \lambda \boldsymbol{w}=\boldsymbol{S}_{w}^{-1}\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)^{\mathrm{T}} \boldsymbol{w}\tag{4-9} λw=Sw−1(m1−m2)(m1−m2)Tw(4-9)
应该注意到, ( m 1 − m 2 ) T w \left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)^{\mathrm{T}} \boldsymbol{w} (m1−m2)Tw是标量。不影响 w \boldsymbol{w} w 的方向,因此可以得到 w \boldsymbol{w} w 的方向是由 S w − 1 ( m 1 − m 2 ) \boldsymbol{S}_{w}^{-1}\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right) Sw−1(m1−m2)决定的,由于我们只关心 w \boldsymbol{w} w 的方向,因此可以取:
w = S w − 1 ( m 1 − m 2 ) (4-10) \boldsymbol{w}=\boldsymbol{S}_{w}^{-1}\left(\boldsymbol{m}_{1}-\boldsymbol{m}_{2}\right)\tag{4-10} w=Sw−1(m1−m2)(4-10)这就是Fisher判别准则下的最优投影方向。
注意:考虑到数值解的稳定性,实践中通常对 S w \boldsymbol{S}_{w} Sw 进行奇异值分解,即: S w = U Σ V T \boldsymbol{S}_{w}=\mathbf{U \Sigma V}^{\mathrm{T}} Sw=UΣVT,这里的 Σ \boldsymbol\Sigma Σ是一个实对角矩阵,其对角线上的元素是 S w \boldsymbol{S}_{w} Sw的奇异值,然后由 S w − 1 = V Σ − 1 U T \mathbf{S}_{w}^{-1}=\mathbf{V} \boldsymbol{\Sigma}^{-1} \mathbf{U}^{\mathrm{T}} Sw−1=VΣ−1UT得到 S w − 1 \mathbf{S}_{w}^{-1} Sw−1
五、拓展到多分类任务中
假设类别变成多个了,那么要怎么改变,才能保证投影后类别能够分离呢?我们之前讨论的是如何将 d d d 维降到一维,现在类别多了,一维可能已经不能满足要求。假设我们有 C C C 个类别,将其投影到 K K K 个基向量。
- 将这 K K K 个向量表示为: W = [ w 1 ∣ w 2 ∣ … ∣ w K ] \boldsymbol{W}=\left[\boldsymbol{w}_{1}\left|\boldsymbol{w}_{2}\right| \ldots | \boldsymbol{w}_{\mathrm{K}}\right] W=[w1∣w2∣…∣wK]
- 投影上的结果表示为: y = [ y 1 , y 2 , … , y k ] \boldsymbol{y}=\left[y_{1}, y_{2}, \dots, y_{k}\right] y=[y1,y2,…,yk];简写之:
y i = w i T x y = W T x {y_{i}}=\boldsymbol{w}_{i}^{T}\boldsymbol{x} \quad \boldsymbol{y}=\boldsymbol{W}^{T} \boldsymbol{x} yi=wiTxy=WTx
我们打算仍然从类间散列度和类内散列度来考虑。为了便于分析,假设样本向量包含2个特征值时,从几何意义上考虑:
| 多分类图 |
|---|
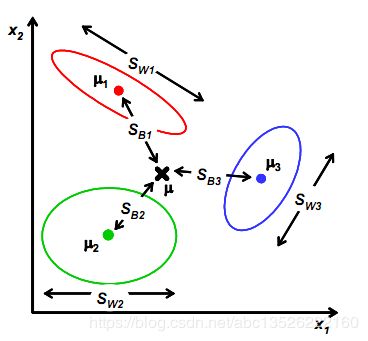
|
假定存在 M M M 个类,属于第 i i i 个类的样本集合为 T i T_{i} Ti, T i T_{i} Ti中的样例的集合为 n i n_{i} ni,则有: ∑ i = 1 M n i = N \sum_{i=1}^{M} n_{i}=N ∑i=1Mni=N ,其中 N N N为样本总数,设 T i T_{i} Ti 表示类别为 i i i, i = 1 , 2 , 3 , 4 , . . . , M i=1, 2, 3, 4,..., M i=1,2,3,4,...,M的样例的集合。这些样例的均值向量为:
μ i = ( μ i ( 1 ) , μ i ( 2 ) , ⋯ , μ i ( n ) ) T = 1 n i ∑ x i ∈ T i x i (5-1) {\boldsymbol{\mu}}_{i}=\left(\mu_{i}^{(1)}, \mu_{i}^{(2)}, \cdots, \mu_{i}^{(n)}\right)^{T}=\frac{1}{n_{i}} \sum_{\boldsymbol{x_{i}} \in T_{i}} \boldsymbol{x}_{i}\tag{5-1} μi=(μi(1),μi(2),⋯,μi(n))T=ni1xi∈Ti∑xi(5-1)
要使同类样本的投影点尽可能的接近,则可以使同类样本投影点方差尽可能小,因此定义类别的类内散度矩阵为:
S i = ∑ x ∈ T i ( x − μ i ) ( x − μ i ) T , i = 1 , 2 , . . . , M (5-2) \boldsymbol{S}_{i}=\sum_{\boldsymbol{x} \in T{i}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)^{\mathrm{T}}, \quad \boldsymbol{i}=1,2,..., M\tag{5-2} Si=x∈Ti∑(x−μi)(x−μi)T,i=1,2,...,M(5-2)
总类内散度矩阵为:
S w = ∑ i = 1 M S i (5-3) \boldsymbol{S}_{\mathrm{w}}=\sum_{i=1}^{M}\boldsymbol{S}_{\mathrm{i}}\tag{5-3} Sw=i=1∑MSi(5-3)
注意: 类别的类内散度矩阵 S i = ∑ x ∈ T i ( x − m i ) ( x − m i ) T , i = 1 , 2 , . . . , M \boldsymbol{S}_{i}=\sum_{\boldsymbol{x} \in T{i}}\left(\boldsymbol{x}-\boldsymbol{m}_{i}\right)\left(\boldsymbol{x}-\boldsymbol{m}_{i}\right)^{\mathrm{T}}, \quad \boldsymbol{i}=1,2,..., M Si=∑x∈Ti(x−mi)(x−mi)T,i=1,2,...,M,实际就等于样本集 T i T_{i} Ti 的协方差矩阵 Σ i \Sigma_{i} Σi,协方差矩阵大小为: n × n n×n n×n,每个样本点的维度为n。
要使异类样本的投影点尽可能的远,则可以使异类样本的中心的投影点尽可能的远,由于这里不止2个中心点,因此不能简单的套用二类LDA的做法(即2个中心点的距离)。这里使用每一类样本集合的中心点距离总的样本中心点 μ \boldsymbol\mu μ的距离作为度量。 考虑到每一类样本集的大小可能不同(密度分布不均;如果某类里面的样本点较多,那么其权重稍大,权重用 N i / N Ni/N Ni/N表示,但由于 J ( w ) J(w) J(w)对倍数不敏感,因此使用 N i N_{i} Ni。),因此定义类间散度矩阵为:
S b = ∑ i = 1 M n i ( μ i − μ ) ( μ i − μ ) T (5-4) \boldsymbol{S}_{\mathrm{b}}=\sum_{i=1}^{M} n_{i}\left(\boldsymbol{\mu}_{i}-\boldsymbol{\mu}\right)\left(\boldsymbol{\mu}_{i}-\boldsymbol{\mu}\right)^{T}\tag{5-4} Sb=i=1∑Mni(μi−μ)(μi−μ)T(5-4)
其中: μ \boldsymbol\mu μ 是所有的样本均值。
μ = 1 N ∑ ∀ x x = 1 N ∑ x ∈ T i n i μ i \boldsymbol\mu=\frac{1}{N} \sum_{\forall x} \boldsymbol x=\frac{1}{N} \sum_{x \in \ T_{i}} n_{i} \boldsymbol\mu_{i} μ=N1∀x∑x=N1x∈ Ti∑niμi
- 具体的推导过程参考:南瓜书
注意: ( m i − μ ) ( m i − μ ) T \left(\boldsymbol{m}_{i}-\boldsymbol{\mu}\right)\left(\boldsymbol{m}_{i}-\boldsymbol{\mu}\right)^{T} (mi−μ)(mi−μ)T也是一个协方差矩阵,它刻画的是第 i i i个类与总体之间的关系!
设 W ∈ R n × ( M − 1 ) \boldsymbol{W} \in \mathbb{R}^{n \times(M-1)} W∈Rn×(M−1)是投影矩阵,经过推导可以得到最大化的目标:(注意:此公式是 ( 4 − 1 ) (4-1) (4−1)的推广形式!)
J = tr ( W T S b W ) tr ( W T S w W ) (5-5) J=\frac{\operatorname{tr}\left(\boldsymbol{W}^{T} \boldsymbol{S}_{b} \boldsymbol{W}\right)}{\operatorname{tr}\left(\boldsymbol{W}^{T} \boldsymbol{S}_{w} \boldsymbol{W}\right)}\tag{5-5} J=tr(WTSwW)tr(WTSbW)(5-5)
- 参考:有些人使用的是行列式,这里使用的是矩阵的迹。 由于我们得到的分子分母都是散列矩阵,要将矩阵变成实数,需要取行列式。又因为行列式的值实际上是矩阵特征值的积,一个特征值可以表示在该特征向量上的发散程度。因此我们使用行列式来计算(此处我感觉有点牵强,道理不是那么有说服力)。
- 其中: tr ( . ) \operatorname{tr}( .) tr(.)表示矩阵的迹,一个矩阵的迹就是一个矩阵的对角线元素之和,它是一个矩阵不变量,也等于矩阵所有的特征值之和。
- 还有一个常用的矩阵不变量,就是矩阵的行列式,它等于矩阵的所有特征值之积。
多分类LDA将样本投影到 M − 1 M-1 M−1维空间,因此它是一种经典的监督降维技术,之所以叫监督是因为对于每个训练样本,我们知道它所属的类别。
六、Fisher实战分析:二分类
6.1、数据生成
- 这里直接用scikit-learn的接口来生成数据:
from sklearn.datasets import make_multilabel_classification
import numpy as np
x, y = make_multilabel_classification(n_samples=20, n_features=2,
n_labels=1, n_classes=1,
random_state=2) # 设置随机数种子,保证每次产生相同的数据。
# 根据类别分个类
index1 = np.array([index for (index, value) in enumerate(y) if value == 0]) # 获取类别1的indexs
index2 = np.array([index for (index, value) in enumerate(y) if value == 1]) # 获取类别2的indexs
c_1 = x[index1] # 类别1的所有数据(x1, x2) in X_1
c_2 = x[index2] # 类别2的所有数据(x1, x2) in X_2
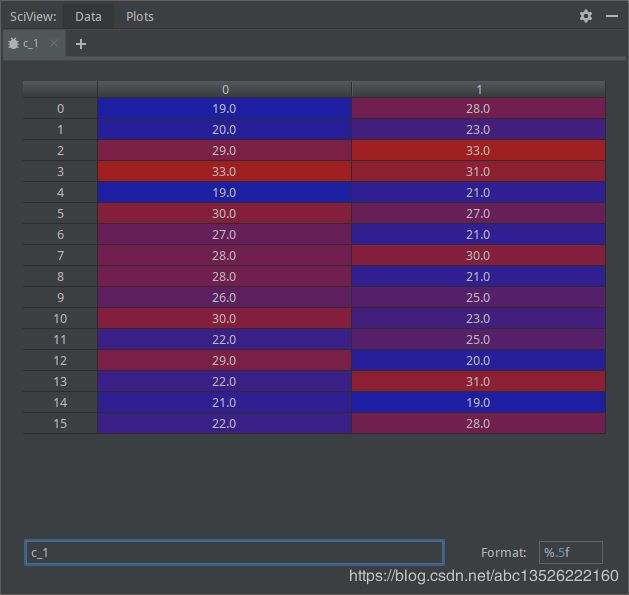
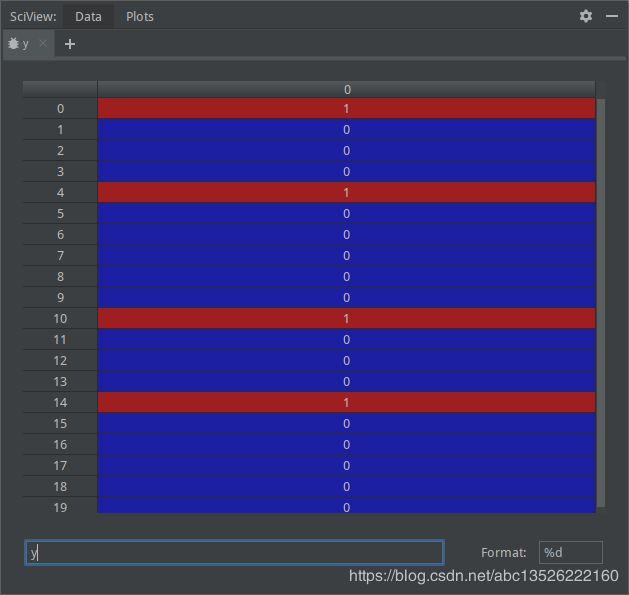
- 断点演示:
| 数 据 x 数据x 数据x | 标 签 y 标签y 标签y |
|---|---|
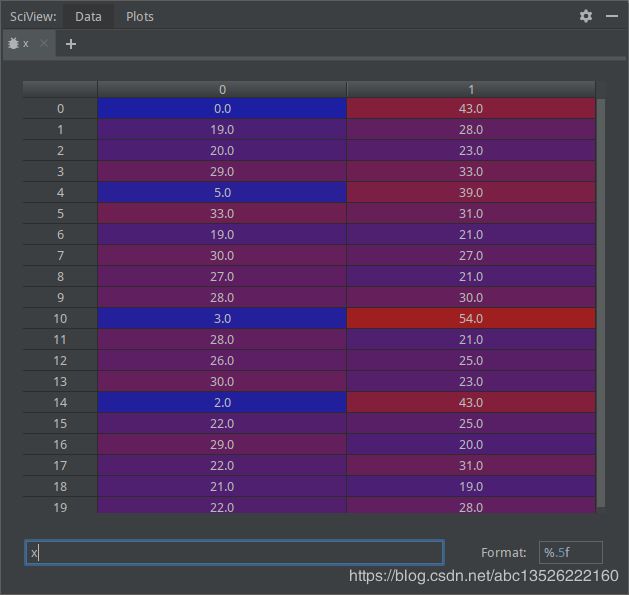
|
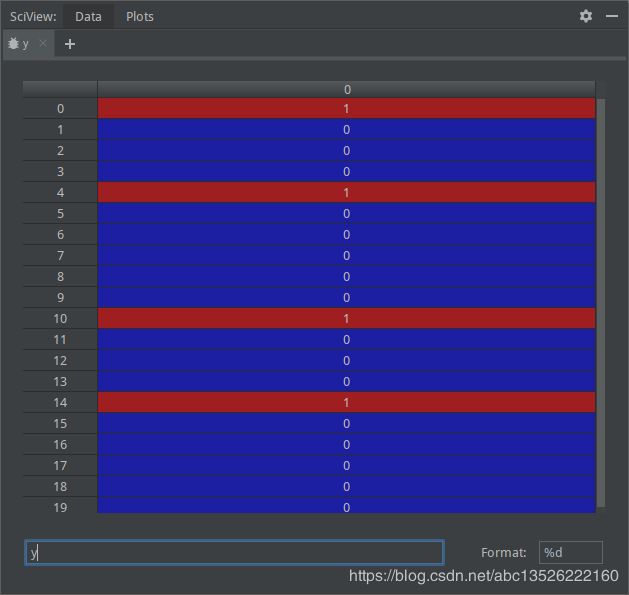
|
| 类 别 1 的 所 有 数 据 ( x 1 , x 2 ) i n X 1 类别1的所有数据(x1, x2) in X_1 类别1的所有数据(x1,x2)inX1 | 类 别 2 的 所 有 数 据 ( x 1 , x 2 ) i n X 2 类别2的所有数据(x1, x2) in X_2 类别2的所有数据(x1,x2)inX2 |
|
|
6.2、fisher算法
注意: 类间散度矩阵也是一个协方差矩阵,他刻画的是第 i i i 和总体之间的关系。
# 2、Fisher算法实现
def cal_cov_and_avg(samples):
"""
给定一个类别的数据,计算协方差矩阵和平均向量
:param samples:
:return:
"""
u1 = np.mean(samples, axis=0)
cov_m = np.zeros((samples.shape[1], samples.shape[1]))
for s in samples:
t = s - u1
cov_m += t*t.reshape(2, 1)
return cov_m, u1
def fisher(c_1, c_2):
"""
fisher算法实现(参考上面的推导公式进行理解)
:param c_1:
:param c_2:
:return:
"""
cov_1, u1 = cal_cov_and_avg(c_1)
cov_2, u2 = cal_cov_and_avg(c_2)
s_w = cov_1 + cov_2 # 总类内离散度矩阵。
u, s, v = np.linalg.svd(s_w) # 下面的参考公式(4-10)
s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
return np.dot(s_w_inv, u1 - u2)
6.3、判断类别
def judge(sample, w, c_1, c_2):
"""
返回值:ture 属于1;false 属于2
:param sample:
:param w:
:param c_1:
:param c_2:
:return:
"""
u1 = np.mean(c_1, axis=0)
u2 = np.mean(c_2, axis=0)
center_1 = np.dot(w.T, u1) # 参考公式(2-8)
center_2 = np.dot(w.T, u2)
pos = np.dot(w.T, sample) # 新样本进来判断
return abs(pos - center_1) < abs(pos - center_2)
w = fisher(c_1, c_2) # 调用函数,得到参数w
out = judge(c_2[1], w, c_1, c_2) # 判断所属的类别。
print(out)
6.4、绘图
# 4、绘图功能
plt.scatter(c_1[:, 0], c_1[:, 1], c='red')
plt.scatter(c_2[:, 0], c_2[:, 1], c='blue')
line_x = np.arange(min(np.min(c_1[:, 0]), np.min(c_2[:, 0])),
max(np.max(c_1[:, 0]), np.max(c_2[:, 0])),
step=1)
line_y = -(w[0]*line_x) / w[1]
plt.plot(line_x, line_y, linewidth=3.0, label = 'fisher boundary line ')
plt.legend(loc='upper right')
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.show()
6.5、运行结果
| 二分类运行结果 |
|---|

|
参考文章
- 周志华《机器学习》
- 张学工《模式识别》
- 杨淑莹《模式识别与智能计算》
- JerryLead-线性判别分析(Linear Discriminant Analysis)(一)
- fisher判别分析原理+python实现
补充:矩阵求导可以参考
- https://blog.csdn.net/daaikuaichuan/article/details/80620518
- https://blog.csdn.net/xtydtc/article/details/51133903
- https://blog.csdn.net/yc461515457/article/details/49682473
- 【机器学习】汇总详解:矩阵的迹以及迹对矩阵求导都是讨论的方阵