ML笔记：PCA(Principal Component Analysis)降维全面解读+python实现！

PCA(Principal Component Analysis)降维全面解读+python实现！

一、数据降维

1.1、维度诅咒问题

许多机器学习问题涉及训练实例的几千甚至上百万个特征，这不仅导致训练非常的缓慢，也让我们很难找到好的解决方案。这个问题通常称为维度诅咒！幸运的是，对现实世界的问题，我们一般可以大量减少特征的数量，将棘手的问题转化为容易解决的问题。例如，MNIST图像：图像边框的像素位上几乎全都是白色，所以我们完全可以在训练集中抛弃这些像素位，也不会丢失太多的信息。
数据降维确实会丢失一些信息（就好比图像压缩为JPEG会降低其质量一样），所以，它虽然能够加速训练，但是也会轻微降低系统的性能。同时它也会让流水线更为复杂，维护难度上升。所以，如果训练太慢，你首先尝试的还是继续使用原始的数据，然后在考虑数据降维。不过在某些情况下，降低训练数据的维度可能会过滤掉一些不必要的噪声和细节，从而导致性能更好（但是通常不会，它只会加速训练）。
除了加速训练，降维对于数据可视化也是非常有用的。降维度降低到两个（或三个），就可以在图形上绘制出高维训练集，通过视觉来检测模式，常常可以获得一些十分重要的洞察，比如说聚类。

1.2、为什么要进行数据降维？

众所周知，数据在低纬下，更容易处理。但是通常情况下我们的数据并不是如此，往往有很多的特征，进而就出现很多问题：

1. 多余的特征会影响或误导学习器
2. 更多的特征意味着更多的参数需要调整，过拟合风险也越大
3. 数据的维度可能只是虚高，真实维度可能比较小
4. 维度越少意味着训练越快，更多的东西可以尝试，能够得到更好的结果
5. 如果我们想要可视化数据，就必须限制在2个或者3个维度上

因此，我们需要通过降维(dimensionality reduction)把无关或冗余的特征删除掉。

1.3、降维的方法

对于数据降维的方法大致有如下这么多：

• 特征筛选
• 特征抽取

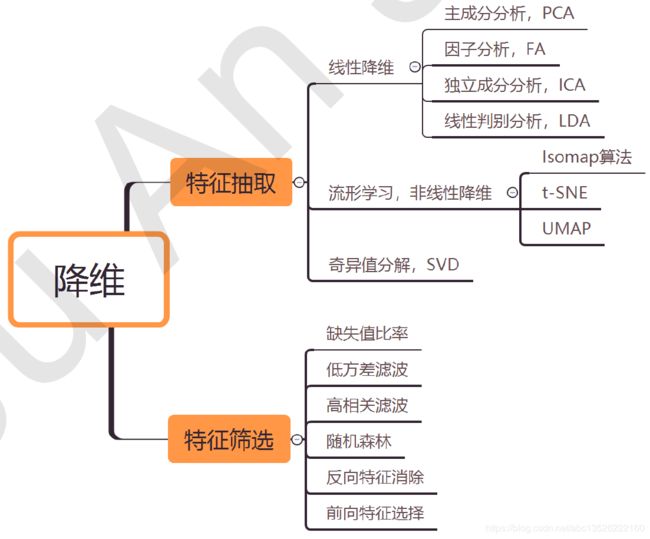
下面主要介绍PCA主成分分析算法。

二、PCA主成分分析

2.1、PCA概述

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法，对于一系列的特征组成的多维向量，多维向量里的某些元素本身没有区分性，比如某个多维向量里的所有元素都是1，或者与1差距不大，那么这个元素本身没有区分性，用它来做特征来区分，贡献非常小。所以我们的目的是找那些变化大的元素，即方差大的那些维，而去掉变化不大的维，从而使特征留下的都是精品，而且计算量变小了。

2.2、PCA降维流程

PCA的主要思想是将n维特征映射到k维上（也就是数据从原来的坐标系转换到新的坐标系，由数据本身决定。转换坐标时，以方差最大的方向作为坐标轴方向，因为数据的最大方差给出了数据的最重要的信息），这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中：第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交且方差次大的方向。 重复该过程，重复次数为原始数据的特征维数，通过这种方式获得的新的坐标系，我们发现，我们发现，大部分方差都包含在前面几(k)个坐标轴中后面的坐标轴所含的方差几乎为0。 于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

• 比如下图中：方差最大的方向作为坐标轴，方差最大意味着包含数据的信息最多，比如下面这个散点图中，找方差最大的方向就是图中的蓝色部分的方向，作为坐标轴。

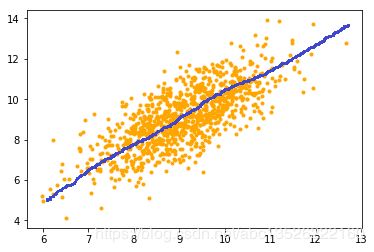
思考： 我们如何得到这些包含最大差异性的主成分方向呢？

• 答案： 事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。
• 同时由于得到协方差矩阵的特征值特征向量有两种方法：①特征值分解协方差矩阵、②奇异值分解协方差矩阵， 所以PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。

提到协方差矩阵，那么就简单介绍一下方差和协方差的关系（参考：ML笔记：机器学习中的协方差矩阵的深入理解！）。然后概括介绍一下特征值分解矩阵原理、奇异值分解矩阵的原理（参考：矩阵论笔记：奇异值分解SVD(Singular Value Decomposition)以及应用总结！）。

2.1、协方差和散度矩阵

• 样本均值：

$$\overline{x}=\frac{1}{n}\sum _{i=1}^N{x}_i\text{\hspace{1em}(1)}$$

• 样本方差：
  $$S^2=\frac{1}{n-1}\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2\text{\hspace{1em}(2)}$$

• 协方差是衡量两个随机变量（同一样本，不同分量）的相关程度。而方差描述的是一维变量：

• 随机变量X和Y之间的协方差可以表示为(协方差反映的是：X和Y之间的协同发展趋势)：
  $$\begin{array}{rl}\mathrm{Cov}(X,Y)& =E[(X-E(X))(Y-E(Y))]\\ & =\frac{1}{n-1}\sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)\end{array}\text{\hspace{1em}(3)}$$

由上面的公式，我们可以得到以下结论：

• 方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况。

• 方差和协方差的除数是n-1,这是为了得到方差和协方差的无偏估计。

• 协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵)。例如，对于3维数据(x,y,z)，计算它的协方差就是：（更详细的可以参考上面的链接！）
  $$\mathrm{Cov}(X,Y,Z)=\left(\begin{array}{ccc}\mathrm{cov}(x,x)& \mathrm{cov}(x,y)& \mathrm{cov}(x,z)\\ \mathrm{cov}(y,x)& \mathrm{cov}(y,y)& \mathrm{cov}(y,z)\\ \mathrm{cov}(z,x)& \mathrm{cov}(z,y)& \mathrm{cov}(z,z)\end{array}\right)\text{\hspace{1em}(4)}$$

对于数据$\mathbf{X}的$散度矩阵$\mathbf{X}{\mathbf{X}}^T$定义为大小为：n×n ，每个样本点的维度为n。

$$\mathbf{S}=\sum _{k=1}^n\left({\mathbf{x}}_k-\mathbf{m}\right){\left({\mathbf{x}}_k-\mathbf{m}\right)}^T\text{\hspace{1em}(5)}$$其中$\mathbf{m}$为均值向量如下：
$$\mathbf{m}=\frac{1}{n}\sum _{k=1}^n{\mathbf{x}}_k\text{\hspace{1em}(6)}$$

2.2、协方差矩阵和散度矩阵的关系

将协方差矩阵乘以系数（n-1）就得到了散度矩阵，所有散度矩阵与协方差矩阵矩阵的作用是一样的，理解了协方差矩阵也就理解了散度矩阵，它们只有一个系数之差而已。因此它们的特征值和特征向量是一样的。这里值得注意的是，散度矩阵是SVD奇异值分解的一步，因此PCA和SVD是有很大联系。

• 实验验证！

import numpy as np

# 默认每一行代表一个随机变量，每列代表随机变量的值,我们希望是每行一个随机变量。
a = np.array(
    [[3,  8,   22],
     [2,  39,  4],
     [26, 15,  11],
     [38, 26,  45],
     [46, 8,   7],
     [6,  30,  41],
     [28, 13,  26],
     [23, 32,  49],
     [0,  34,  3],
     [16, 37,  22]])
# python自带的函数求出协方差
# rovar默认为True，设为False表示每一列变量，这样每一列表示维数。
# 10为样本的个数，3为样本的维数
print("自带函数求得协方差矩阵如下：\n",np.cov(a, rowvar = False))

# 自己求出来类内散度矩阵
dim1 = a[:,0]
dim2 = a[:,1]
dim3 = a[:,2]
print("协方差cov1_1:", np.sum((dim1 - np.mean(dim1)) * (dim1 - np.mean(dim1))) / (len(dim1) - 1))
print("协方差cov2_2:", np.sum((dim2 - np.mean(dim2)) * (dim2 - np.mean(dim2))) / (len(dim1) - 1))
print("协方差cov3_3:", np.sum((dim3 - np.mean(dim3)) * (dim3 - np.mean(dim3))) / (len(dim1) - 1))
print("协方差cov1_2:", np.sum((dim1 - np.mean(dim1)) * (dim2 - np.mean(dim2))) / (len(dim1) - 1))
print("协方差cov1_3:", np.sum((dim1 - np.mean(dim1)) * (dim3 - np.mean(dim3))) / (len(dim1) - 1))
print("协方差cov2_3:", np.sum((dim2 - np.mean(dim2)) * (dim3 - np.mean(dim3))) / (len(dim1) - 1))

# 注意python求解和matlab结果不一样，下面第一种是相同的，第二种不同，一个是无偏估计，一个最大似然估计。
# matlab中计算协方差是首先加了n项，然后除以n或n-1，cov(x)呢是除以n-1，cov(x,1)呢是除以n。
# print("对角线", np.var(dim1) / (len(dim1) - 1) * len(dim1))
# print("对角线", np.var(dim2) / (len(dim1) - 1) * len(dim1))
# print("对角线", np.var(dim3) / (len(dim1) - 1) * len(dim1))
#
# print(np.var(dim1))
# print(np.var(dim2))
# print(np.var(dim3))

# 类内散度矩阵
mean_all = np.mean(a, axis=0)
sw = 0

for i in range(len(dim1)):
    sw += np.matmul(np.reshape(a[i, :]- mean_all, [3, 1]), np.reshape(a[i, :]- mean_all, [1, 3]))
print("类内散度矩阵如下：\n", sw)
print("类内散度矩阵除以(n-1)如下：\n", sw/9)

• 运行结果如下：

ssh://[email protected]:22/home/zhangkf/anaconda3/envs/tf2gpu/bin/python -u /home/zhangkf/tf2/TF1/test.py
自带函数求得协方差矩阵如下：
 [[257.73333333 -92.17777778  57.88888889]
 [-92.17777778 145.73333333  23.22222222]
 [ 57.88888889  23.22222222 295.11111111]]
协方差cov1_1: 257.73333333333335
协方差cov2_2: 145.73333333333332
协方差cov3_3: 295.1111111111111
协方差cov1_2: -92.17777777777778
协方差cov1_3: 57.88888888888888
协方差cov2_3: 23.22222222222223
类内散度矩阵如下：
 [[2319.6 -829.6  521. ]
 [-829.6 1311.6  209. ]
 [ 521.   209.  2656. ]]
类内散度矩阵除以(n-1)如下：
 [[257.73333333 -92.17777778  57.88888889]
 [-92.17777778 145.73333333  23.22222222]
 [ 57.88888889  23.22222222 295.11111111]]

Process finished with exit code 0

• 从输出结果：我们可以发现协方差矩阵乘以系数n-1就得到了散度矩阵，或者散度矩阵除以n-1。

2.3、特征值分解（EVD）原理

(1) 特征值与特征向量

• 如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：
  $$\mathbf{A}v=\lambda v$$
• 其中，λ是特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。

(2) 特征值分解矩阵

• 对于矩阵A，有一组特征向量v，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵v分解为如下式：
  $$\mathbf{A}=\mathbf{Q}\mathbf{\Sigma }{\mathbf{Q}}^{-1}$$
• 其中，Q是矩阵A的特征向量组成的矩阵，$\mathbf{\Sigma }$则是一个对角阵，对角线上的元素就是特征值。
• 具体了解这一部分内容看我的：矩阵论笔记：奇异值分解SVD(Singular Value Decomposition)以及应用总结！

2.4、奇异值分解（SVD）原理

奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解：
$$A=U\Sigma V^T$$

• 假设A是一个m×n的矩阵，那么得到的U是一个m×m的方阵，U里面的正交向量被称为左奇异向量。$\Sigma$是一个m×n的矩阵，$\Sigma$除了对角线其它元素都为0，对角线上的元素称为奇异值。$V^T$是v的转置矩阵，是一个n×n的矩阵，它里面的正交向量被称为右奇异值向量。 而且一般来讲，我们会将$\Sigma$上的值按从大到小的顺序排列。

• SVD分解矩阵A的步骤：具体了解这一部分内容看我的：矩阵论笔记：奇异值分解SVD(Singular Value Decomposition)以及应用总结！

三、PCA算法两种实现方法

3.1、基于特征值分解协方差矩阵实现PCA算法

输入：：数据集$\mathbf{X}=\left\{x_1,x_2,x_3,\dots ,x_n\right\}$，需要降到k维。

• (1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。
• (2) 计算协方差矩阵$\frac{1}{n}\mathbf{X}{\mathbf{X}}^T$(注意：这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。)
• (3) 用特征值分解方法求协方差矩阵$\frac{1}{n}\mathbf{X}{\mathbf{X}}^T$的特征值与特征向量。
• (4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
• (5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。

总结：
（1）关于这一部分为什么用$\frac{1}{n}\mathbf{X}{\mathbf{X}}^T$，这里面有这里面含有很复杂的线性代数理论推导，想了解具体细节的可以看下面这篇文章。CodingLabs - PCA的数学原理
（2）关于为什么用特征值分解矩阵，是因为$\frac{1}{n}\mathbf{X}{\mathbf{X}}^T$是方阵，能很轻松的求出特征值与特征向量。当然，用奇异值分解也可以，是求特征值与特征向量的另一种方法。

3.1.1、举例

举个例子：以$\mathbf{X}$为例，每列表示一个样本，每个样本维度为2，我们用PCA方法将维度从2将到1。
$$\mathbf{X}=\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)$$

• (1) 因为$\mathbf{X}$矩阵的每列已经是零均值，所以不需要去平均值。
• (2) 求协方差矩阵：
  $$\mathbf{C}=\frac{1}{5}\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)\left(\begin{array}{cc}-1& -2\\ -1& 0\\ 0& 0\\ 2& 1\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}\frac{6}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}\end{array}\right)$$
• (3) 求协方差矩阵的特征值与特征向量。求解后的特征值为：${\lambda }_1=2,{\lambda }_2=\frac{2}{5}$；对应的特征向量为：$${\mathbf{c}}_1=\left(\begin{array}{l}1\\ 1\end{array}\right),{\mathbf{c}}_2=\left(\begin{array}{c}-1\\ 1\end{array}\right)$$
• 其中对应的特征向量分别是一个通解，${\mathbf{c}}_1$ 和 ${\mathbf{c}}_2$可以取任意实数。那么标准化后的特征向量为：
  $$\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right),\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$$
• (4) 矩阵P为：
  $$\mathbf{P}=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)$$
• (5) 最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：
  $$\mathbf{Y}=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)=\left(\begin{array}{ccccc}-\frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& \frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right)$$
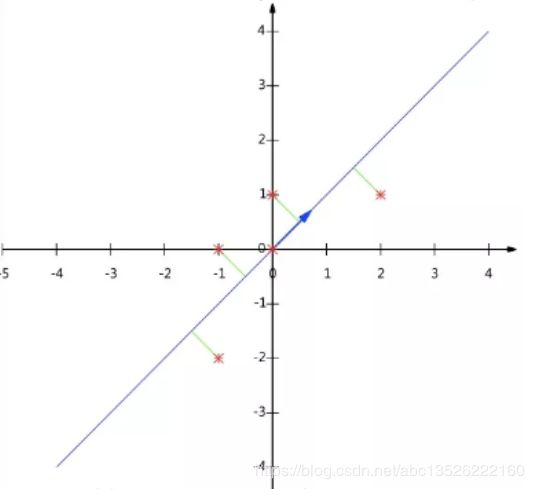
  结果如图1所示：

图1：数据矩阵X降维投影结果
注意：如果我们通过特征值分解协方差矩阵，那么我们只能得到一个方向的PCA降维。这个方向就是对数据矩阵X从行(或列)方向上压缩降维。

3.2、基于SVD分解协方差矩阵实现PCA算法

输入：：数据集$\mathbf{X}=\left\{x_1,x_2,x_3,\dots ,x_n\right\}$，需要降到k维。

• (1) 去平均值，即每一位特征减去各自的平均值。
• (2) 计算协方差矩阵。
• (3) 通过SVD计算协方差矩阵的特征值与特征向量。
• (4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
• (5) 将数据转换到k个特征向量构建的新空间中。

在PCA降维中，我们需要找到样本协方差矩阵$\mathbf{X}{\mathbf{X}}^T$的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$\mathbf{X}{\mathbf{X}}^T$。当样本数多、样本特征数也多的时候，这个计算还是很大的。当我们用到SVD分解协方差矩阵的时候，SVD有两个好处：

• 有一些SVD的实现算法可以先不求出协方差矩阵$\mathbf{X}{\mathbf{X}}^T$也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解。
• 注意到PCA仅仅使用了我们SVD的左奇异矩阵，没有使用到右奇异值矩阵，那么右奇异值矩阵有什么用呢？
• 假设我们的样本是m×n的矩阵$\mathbf{X}$，如果我们通过SVD找到了矩阵${\mathbf{X}}^T\mathbf{X}$最大的k个特征向量组成的k×n的矩阵${\mathbf{V}}^T$ ,则我们可以做如下处理：
  $${\mathbf{X}}_{m\times k}^{\prime }={\mathbf{X}}_{m\times n}{\mathbf{V}}_{n\times k}^T$$

可以得到一个m×k的矩阵${\mathbf{X}}^{\prime }$,这个矩阵和我们原来m×n的矩阵$\mathbf{X}$相比，列数从n减到了k，可见对列数进行了压缩。也就是说，左奇异矩阵可以用于对行数的压缩；右奇异矩阵可以用于对列(即特征维度)的压缩。这就是我们用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维(即行和列两个方向)。

四、python实现PCA算法

4.1、PCA的python实现