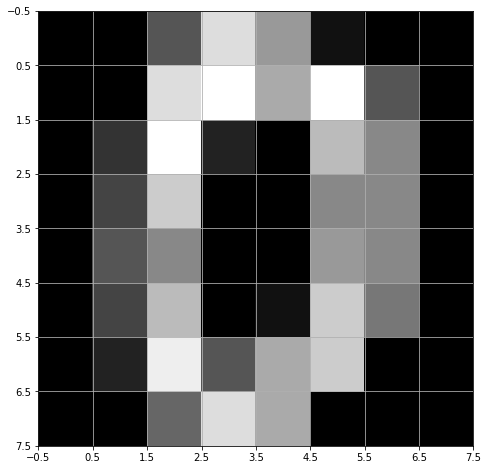线性代数在数据科学中的十大强大应用(二)
译者 | 磐石
来源 | analyticsvidhya.com
系列目录:
为什么学习线性代数
机器学习中的线性代数
损失函数
正则化
协方差矩阵
支持向量机分类器
降维中的线性代数
主成分分析(PCA)
奇异值分解(SVD)
自然语言处理中的线性代数
词嵌入(Word Embeddings)
潜在语义分析
计算机视觉中的线性代数
图像用张量表示
卷积与图像处理
自然语言处理(NLP)
由于过去18个月自然语言处理(NLP)取得的各项重大突破,NLP是目前数据科学领域最热门的领域。
让我们看一下NLP中线性代数的几个有趣的应用。这应该有助于引起你的思考!
7. 图嵌入
文本的元属性,如:“字数”,“特殊字符数”等。
使用“词性标签”和“语法关系”(如专有名词的数量)等文本数据NLP属性
词向量符号或词嵌入(Word Embeddings)
词嵌入(Word Embeddings)是自然语言处理(NLP)中语言模型与表征学习技术的统称。概念上而言,它是指把一个维数为所有词的数量的高维空间嵌入到一个维数低得多的连续向量空间中,每个单词或词组被映射为实数域上的向量。这些表示是通过在大量文本上训练不同的神经网络而获得的,这些文本被称为语料库。它们还有助于分析单词之间的句法相似性:
Word2Vec和GloVe是两种流行词嵌入工具。
在使用Word2Vec进行一些轻度预处理后,我在莎士比亚语料库(https://norvig.com/ngrams/shakespeare.txt)上训练了我的模型,并获得了“世界”这个词的词嵌入(word embedding):
太酷了!但更令人惊喜的是我从中为“词汇”绘制下图,可以观察到语法相似的单词更加接近了。我在图中圈出了一些这样的词汇。虽然结果并不完美,但它们仍然非常惊人:
8. 潜在语义分析(LSA)
当你听到这组词语时- “王子,王室,国王,贵族”,你首先想到的是什么?这些不同的词几乎都是同义词。
现在,考虑以下句子:
The pitcher of the Home team seemed out of form (主队的“投手”似乎不合格)
There is a pitcher of juice on the table for you to enjoy(桌子上有一“罐”果汁供您享用)
“pitcher”这个词基于两个句子语境分别有不同的含义。 这意味着第一句中的“棒球运动员”和第二句中的“一罐果汁”。
这些单词对于我们人类来说很容易通过多年的语言经验来理解。但是对于机器呢?在这里,NLP概念--主题模型将发挥作用:
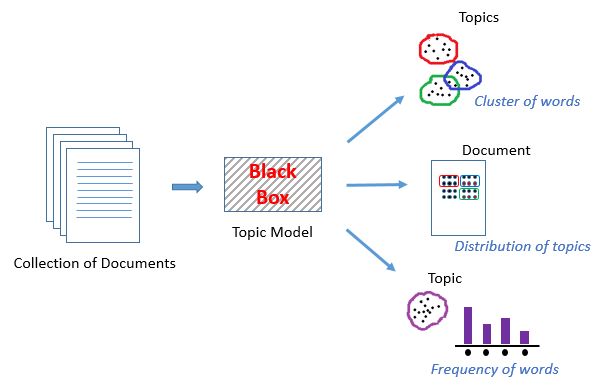
主题模型是一种实现在各种文本文档中查找主题的无监督技术。这些主题只不过是相关单词的集群,每个文档可以有多个主题。主题模型输出多种主题,以及它们在每个文档中的分布与它包含的各种单词的频率。
潜在语义分析(LSA)或潜在语义索引是主题建模的技术之一。它也是奇异值分解(SVD)的另一种应用。
潜在意味着'隐藏'。正如其名称一样,LSA试图通过利用单词周围的上下文从文档中捕获隐藏的主题。
LSA的实现步骤简要介绍如下:
首先,为您的数据生成Document-Term矩阵
使用SVD将矩阵分解为3个矩阵:
文档主题矩阵
主题重要性对角矩阵
主题词矩阵
根据主题的重要性截断矩阵
计算机视觉(CV)
深度学习的另一个领域--计算机视觉正在蓬勃发展。如果您希望将技能组扩展到表格数据之外,那么请学习如何处理图像。
接着梳理下边几个概念将有助于拓宽目前对机器学习的理解,对cv相关岗位的面试也有一定的帮助。
9. 图像表示为张量
数字图像由被称为“像素”的小不可分割单元组成。如下图:
这个数字零的灰度图像由8×8=64个像素组成。每个像素的值在0到255的范围内。值0表示黑色像素,255表示白色像素。
进一步来看,mxn灰度图像可以由具有m行和n列的2D矩阵表示,其中每个单元格包含相应的像素值:
那么彩色图像呢?彩色图像通常存储在RGB通道中。每个图像可以被认为是由三个2D矩阵表示,相对应每个R,G和B通道各一个。R通道中的像素值0表示红色的零强度,255表示红色的全强度。
然后,对应到图像中,则每个像素值是三个通道中相应值的组合:
实际上,不是使用3个矩阵而是使用张量来表示图像,张量是广义的n维矩阵。对于RGB图像,使用三阶张量来表示。想象一下,正如三个二维矩阵一个接一个堆叠:
10. 卷积与图像处理
2D卷积是图像处理中非常重要的操作。实现步骤如下:
从一个小的权重矩阵开始,称为内核(kernel)或滤波器(filter)
在2D输入数据上滑动此内核,执行逐元素乘法
添加获得的值并将总和放在单个输出像素中
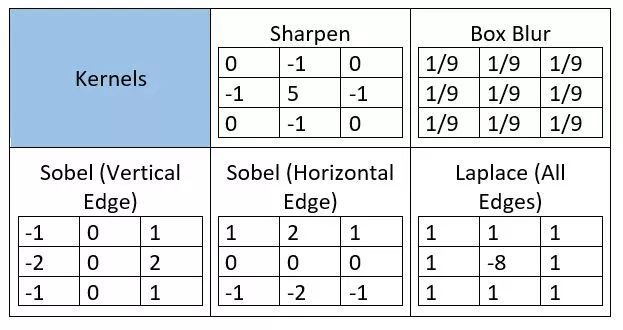
该功能虽然看起来有点复杂,但它广泛应用于各种图像处理操作中。如:锐化、图像模糊(blurring)和边缘检测。我们只需要知道完成任务所需使用的内核(kernel)是哪一个,下面列举了一些常用的内核(kernel):
大家可以通过此链接(https://drive.google.com/file/d/1aM4otWKSsDz1Rof3LZkY055YkYXeO-vf/view)下载文章中使用的示例图像, 并使用上面的代码和内核(kernel)自己尝试上述图像处理操作。
这是迄今为止最炫酷的线性代数在数据科学中的应用之一。
结束笔记
线性代数在数据科学中无处不在,希望本系列文章列举的这些应用可以激励大家进一步学习了解技术背后的数学知识。同时也希望可以帮大家理清思路和对上述算法有更进一步的认识。