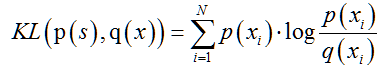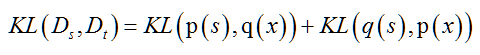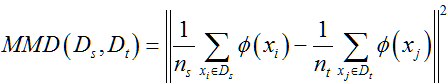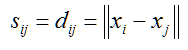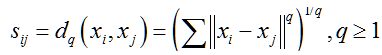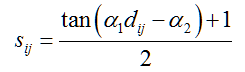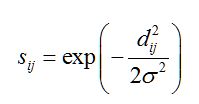源领域和目标领域过程相似性分析
1. 过程相似性定义
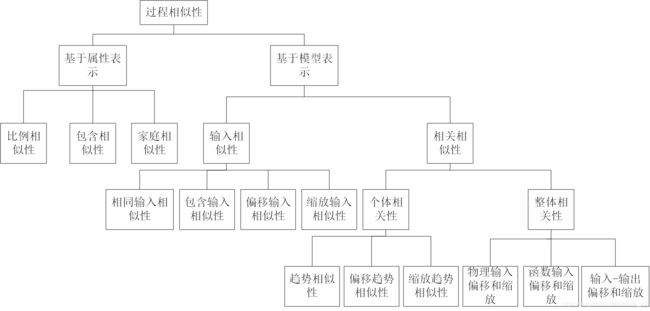
Lu等在《Process Similarity and Developing New Process Models Through Migration》根据有限的过程属性集,或者根据这些属性之间的关系来描述特定过程,分为基于属性的表示方法和基于模型的表示方法。基于属性的表示方法是利用有限属性及其属性值来表示,主要关注工艺设备和过程条件;基于模型的表示方法是利用过程属性之间的关系来表示,主要反映过程条件和输出特性之间的关系。这两种类型的过程表示将过程相似性分类为如下图所示。
(1)过程相似性
定义1:具有相同结构的两个过程被认为属于一种类型,并且表示为结构相似;否则,这些过程在结构上是不同的。显然,属于一种类型的过程在集合中具有相同数量的属性,并且两个集合中的属性是对属性。
下式给出了两个磨矿分级过程的实例,两者都具有相同的生产组件,例如旋流器,矿池,给矿泵等,因此这两个过程在结构上相似。其中上标1和2分别代表过程1和2。显然,这两个过程在结构上相似是模型迁移的前提条件。
定义2:如果它们彼此对应并且它们与属性集中的其他属性处于相同的关系,则将不同过程的两个属性表示为对属性。如定义1,公式中的属性旋流器1和旋流器2是对属性。
(2)基于属性的表示
定义:过程P由基于属性的表示中的一组过程属性和属性值表示,定义为:
其中,A是一组有限的过程属性,反映了过程的性质,包括进料,操作设备,环境条件等;V是对应的属性值。
(3)基于模型的表示
定义:一个过程由一组过程条件,质量属性及其在基于模型的表示中的关系表示:
其中,X是一组操作条件或输入变量;Y是一组质量变量,响应变量或输出变量; R是由过程原理控制的X和Y之间的关系。通常,R可以通过任何建模方法开发。
(4)基于属性相似性分类
定义1:如果两个过程对属性的全部或部分具有相似的值,则称两个过程具有属性相似性。否则,当没有值匹配时,过程就不同了。属性相似性可以分为比例相似性,包含相似性和家庭相似性。
定义2:如果过程1的全部或部分属性值直接从过程2的对应对属性值缩放,则该过程具有比例相似性。
定义3:如果描述过程1的所有或一些属性值是过程2的对应对属性值的子集,则该过程具有包含性相似性。
定义4:如果两个过程的所有或一些对属性具有属于某些类的值,则该过程具有家庭相似性。
(5)基于模型相似性分类
定义1:如果两个过程的一些或所有过程变量的操作范围具有相同的范围,则过程具有相同输入相似性。
定义2:如果过程1的一些或所有过程变量的操作范围包括在过程2的相应操作范围或包括过程2的相应操作范围,则过程具有包含输入相似性,
定义3:如果过程1中的一些或所有过程变量的操作范围从过程2中的相应操作范围偏移,则过程具有偏移输入相似性。
定义4:如果过程1中的一些或所有过程变量的操作范围从过程2中的相应操作范围缩放,则过程具有缩放输入相似性。
定义5:如果在输入变量的相同操作范围内,两个过程模型的响应曲线具有相同的行为但幅度不同,则过程模型具有趋势相似性或模式相似性。
定义6:如果在两个过程模型中输入变量的操作范围发生偏移时,响应曲线具有相同的行为但幅度不同,则过程模型具有偏移趋势相似性。
定义7:如果当输入变量的范围在两个过程模型之间缩放时,响应曲线也会缩放,则过程模型具有缩放趋势相似性。
定义8:给定过程1和过程2的模型,如果过程2的输入是过程1的输入偏移和缩放,则过程2是过程1的物理输入偏移和比例。
定义9:如果过程2比例和偏移参数与定义8中的不同,而由新数据获得,则过程2是过程1的函数输入偏移和比例。
定义10:如果通过下式处理描述偏移和比例,则过程2是过程1的输入-输出偏移和比例。
2. 过程相似性度量
模型迁移学习迁移至目标领域知识的多少,取决于源领域与目标领域之间的相似性,即领域间越相似,则目标领域可获取的知识越多,所以模型迁移学习的关键问题是领域间具有相关性。因此,本文在此对领域间相似性度量的常用方法进行简单描述。
目前,对于领域间分布差异的度量虽未有一个统一的方法,但却有一些常用的方法可帮助我们发展此理论,比如KL散度、布雷格曼散度、最大均值差异等方法。
(1)KL散度
KL散度(KuLLback-Leibler Divergence,KL)是一种量化两种概率分布和之间差异的度量方法,又叫相对熵或者KL熵。在概率学和统计学上,经常使用一种更简单的、近似的分布来替代观察数据或者太复杂的分布。KL散度本来是用于度量一个分布来近似另一个分布所损失的信息,在迁移学习领域可用来度量各领域分布之间的距离。若源领域的分布为,目标领域的分布为,则和之间基于KL散度度量的分布差异为:
此公式是由信息熵公式通过信息损失的度量推导而来,从KL散度的计算公式可以看出它不符合对称性,因为其不是距离的度量。所以,在迁移学习中,通常采用以下公式来度量领域间的分布差异:
(2)布雷格曼散度
布雷格曼散度(Bregman Discrepancy)是一种类似距离度量的方式,用于衡量分布之间差异的大小[67],是以损失函数或者失真函数作为目标函数。假设源领域和目标领域在两种分布下的两个样本点分别为和,可认为点是点的失真点或者近似点,也可以认为点是点添加一些噪声叠加形成的。所以,目标函数是由点近似点的损失最小化。若给定一个严格的凸函数,则和之间的布雷格曼散度通过下面的公式给出:
其中,是在上的梯度,是和之间的內积。公式中的后半部分表示函数在附近的线性部分,布雷格曼散度则是一个函数与的线性近似之间的差,使用不同的可以得到不同的布雷格曼散度。
(3)最大均值差异
最大均值差异(Maximum Mean Discrepancy,MMD)是通过计算源领域和目标领域数据集均值点间的距离来度量它们之间的分布差异程度[68]。基本假设是:若生成样本空间的函数为,且两个分布生成的样本在上对应的均值相等,则认为这两个分布属于同一个分布。最大均值差异通过下面的公式给出:
以上为对领域间分布差异的度量,也可通过直接计算领域间数据样本之间的相似程度来确定领域之间的相似性,这两种思路是截然不同的。计算样本相似性的方法有:
(1)欧式(Euclid)距离法:任意两个数据点和之间的相似性定义为两个数据点之间的欧式距离:
(2)明氏(Minkowski)距离法:任意两个数据点xi和xj之间的相似性定义为两个数据点之间的明式距离:
当q取1、2、无穷时,分别得到绝对距离、欧氏距离和切比雪夫(Chebyshev)距离。
(3)马氏(Mahalanosi)距离法:任意两个数据点和之间的相似性定义为两个数据点之间的马式距离:
其中,是协方差矩阵。马氏距离虽然克服了欧氏距离同等对待每一个属性的缺点,但是由于要计算协方差矩阵,计算量较大,对于大规模数据处理复杂度高。
(4)正切值法:任意两个数据点xi和xj之间的相似性可通过下式表示:
其中,a1,a2为常量。
(5)负指数法或RBF核函数法:通过下式定义任意两个数据点和之间的相似性:
其中,delta为常量。
3. 代码实现
1. 将源领域和目标领域数据集各自使用PCA降维为二维、三维特征,然后在二维空间、三维空间可视化,即将每一个样本以散点的形式在空间中表现出来,通过观察对比两个领域的散点分布来分析两个领域的分布是否具有差异性:
from mpl_toolkits.mplot3d import Axes3D from numpy import *
import pandas as pd
import matplotlib.pyplot as plt
#PCA降维
def pca(dataMat,topNfeat=9999999):
meanVals=mean(dataMat,axis=0)
#print("均值矩阵: ",meanVals)
meanRemoved=dataMat-meanVals
#print("中心化后的矩阵: ",shape(meanRemoved))
covMat=cov(meanRemoved,rowvar=0)
eigVals,eigVects=linalg.eig(mat(covMat))
#print("特征值: ",eigVals)
eigValInd=argsort(eigVals)
#print("排序后的特征值: ",eigValInd)
eigValInd=eigValInd[:-(topNfeat+1):-1]
#print("选择最大的前n个特征值的索引:",eigValInd)
redEigVects=eigVects[:,eigValInd]
#print("选择最大的前n个特征向量",redEigVects)
lowDataMat=meanRemoved*redEigVects
return lowDataMat
#读取CSV文件
srcFrame = pd.read_csv('OGSrc.csv')
tarFrame = pd.read_csv('OGTar.csv')
#将DataFrame类型转化为数组类型
srcData = srcFrame.values
tarData = tarFrame.values
#OG源领域和目标领域数据分别降维
lowSrcData = pca(srcData,3)
lowTarData = pca(tarData,3)
#获取OG各个领域数组的各列数据
src_f1 = transpose(lowSrcData)[0].tolist()[0]
src_f2 = transpose(lowSrcData)[1].tolist()[0]
src_f3 = transpose(lowSrcData)[2].tolist()[0]
tar_f1 = transpose(lowTarData)[0].tolist()[0]
tar_f2 = transpose(lowTarData)[1].tolist()[0]
tar_f3 = transpose(lowTarData)[2].tolist()[0]
ax = plt.subplot(111, projection='3d')
#源领域和目标领域对应的三维散点图
ax.scatter(src_f1, src_f2, src_f3, c='r')
ax.scatter(tar_f1, tar_f2, tar_f3, c='k')
ax.set_xlabel('feature1')
ax.set_ylabel('feature2')
ax.set_zlabel('feature3')
plt.show()2. KL散度(Kullback-Leibler Divergence)
from numpy import *
import pandas as pd
import scipy.stats
#KL散度
def kl(srcArr, tarArr):
m,n = srcArr.shape
result = 0;
for i in range(m):
result += sum( srcArr[i]*(log(srcArr[i])-log(tarArr[i])) )
# result += scipy.stats.entropy( srcArr[i], tarArr[i] )
return result
#读取CSV文件
srcFrame = pd.read_csv('OGSrc.csv')
tarFrame = pd.read_csv('OGTar.csv')
#将DataFrame类型转化为数组类型
srcData = srcFrame.values
tarData = tarFrame.values
print( srcData.shape, tarData.shape )
result = kl(srcData, tarData)3. 最大均值差异
from numpy import *
import pandas as pd
#高斯核
def gaussianKernel(xArr,yArr,s):
temp = sqrt(sum((xArr-yArr)**2))
return exp(-(temp/s))
def mmd(srcArr, tarArr, sigma):
s = 2*(sigma**2)
m = srcArr.shape[0]
n = tarArr.shape[0]
result1 = 0
result2 = 0
result3 = 0
for i in range(m):
for j in range(m):
result1 += gaussianKernel(srcArr[i], srcArr[j], s)
for i in range(m):
for j in range(n):
result2 += gaussianKernel(srcArr[i], tarArr[j], s)
for i in range(m):
for j in range(n):
result3 += gaussianKernel(tarArr[i], tarArr[j], s)
print( result1, result2, result3 )
return 1/(m**2)*result1 - 2/(m*n)*result2 + 1/(n**2)*result3
#读取CSV文件
srcFrame = pd.read_csv('OGSrc.csv')
tarFrame = pd.read_csv('OGTar.csv')
#将DataFrame类型转化为数组类型
srcData = srcFrame.values
tarData = tarFrame.values
print( srcData.shape, tarData.shape )
sigma = 0.1
print( mmd(srcData, tarData, sigma) )