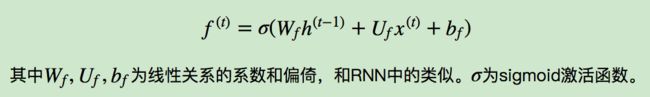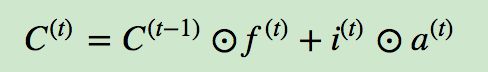循环神经网络及其变体的学习与博客总结
循环神经网络广泛的用于自然语言处理中的语音识别,手写书别以及机器翻译等领域。它有很多变体,比如LSTM和GRU,这一部分还涉及到Seq-2-Seq、Encoder-Decoder 和Attention知识点,总之内容很多,需要细学与总结。
这一部分的博客主要来自:
刘建平大牛的 RNN与前向-反向算法:https://www.cnblogs.com/pinard/p/6509630.html
LSTM与前向-反向算法:https://www.cnblogs.com/pinard/p/6519110.html
知乎的AI Insight 专栏 :https://zhuanlan.zhihu.com/p/28054589
Jason大神的 RNN 简介: https://machinelearningmastery.com/crash-course-recurrent-neural-networks-deep-learning/
因为我这一块还没有太多的实践经验,这篇博客多是理论理解和总结为主,所以没有太多自己的见解,多是对以上博客的摘抄和总结,为自己日后使用方便。如果之后有一些实践上的trick,再来分享。
目录
经典的RNN结构
与输入-输出有关的问题
Attention
RNN的前向传播算法
RNN的反向传播算法
RNN存在的问题
LSTM的结构
遗忘门
输入门
细胞状态更新
输出门
LSTM的前向-反向传播算法
GRU的结构
双向LSTM/GRU
经典的RNN结构
DNN和CNN中,训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决,就是训练样本输入是连续的序列,且序列的长短不一,比如基于时间的序列:一段段连续的语音,一段段连续的手写文字。这些序列比较长,且长度不一,比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。
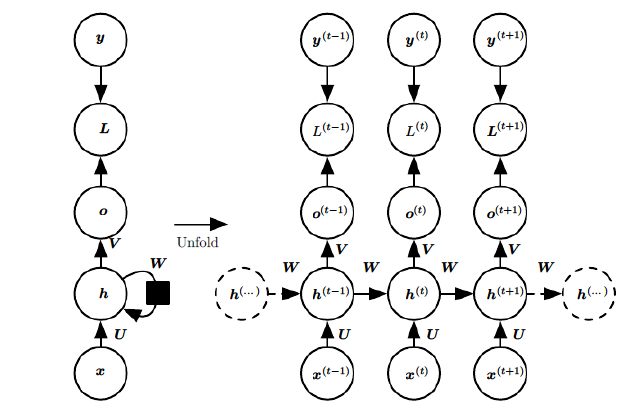
而对于这类问题,RNN则比较的擅长。那么RNN是怎么做到的呢?RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引τ的。对于这其中的任意序列索引号t,它对应的输入是对应的样本序列中的x(t)。而模型在序列索引号t位置的隐藏状态h(t),则由x(t)和在t−1位置的隐藏状态h(t−1)共同决定。在任意序列索引号t,我们也有对应的模型预测输出o(t)。通过预测输出o(t)和训练序列真实输出y(t),以及损失函数L(t),我们就可以用DNN类似的方法来训练模型,接着用来预测测试序列中的一些位置的输出。
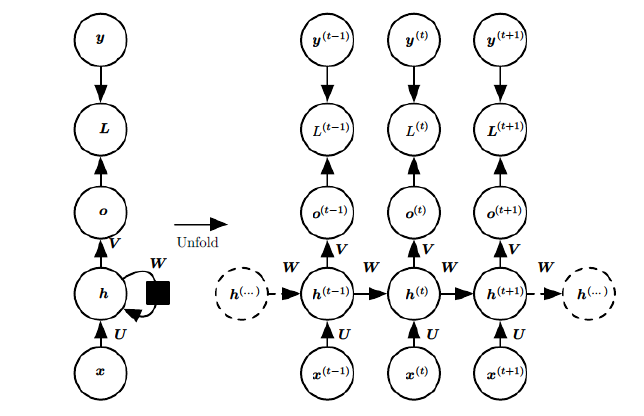
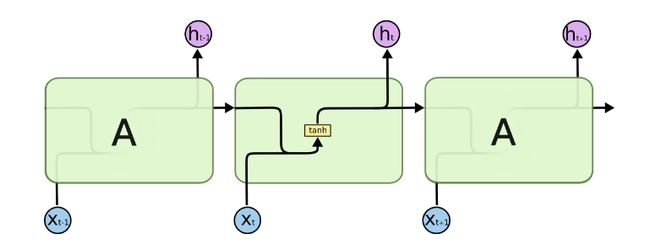
上图中左边是RNN模型没有按时间展开的图,如果按时间序列展开,则是上图中的右边部分。我们重点观察右边部分的图。
这幅图描述了在序列索引号tt附近RNN的模型。其中:
1)x(t)代表在序列索引号t时训练样本的输入。同样的,x(t−1)和x(t+1)代表在序列索引号t−1和t+1时训练样本的输入。
2)h(t)代表在序列索引号t时模型的隐藏状态,为了建模序列问题,RNN引入了隐状态h(hidden state)的概念,h可以对序列形的数据提取特征,接着再转换为输出。h(t)由x(t)和h(t−1)共同决定。
3)o(t)代表在序列索引号t时模型的输出。o(t)只由模型当前的隐藏状态h(t)决定。
4)L(t)代表在序列索引号t时模型的损失函数。
5)y(t)代表在序列索引号t时训练样本序列的真实输出。
6)U,W,V这三个矩阵是我们的模型的线性关系参数,它在整个RNN网络中是共享的,这点和DNN很不相同。 也正因为是共享了,它体现了RNN的模型的“循环反馈”的思想。
同时注意到输入和输出序列必须要是等长的。
由于这个限制的存在,经典RNN的适用范围比较小,但也有一些问题适合用经典的RNN结构建模,如:
- 计算视频中每一帧的分类标签。因为要对每一帧进行计算,因此输入和输出序列等长。
- 输入为字符,输出为下一个字符的概率。这就是著名的Char RNN(详细介绍请参考:The Unreasonable Effectiveness of Recurrent Neural Networks,Char RNN可以用来生成文章,诗歌,甚至是代码,非常有意思)。
与输入-输出有关的问题
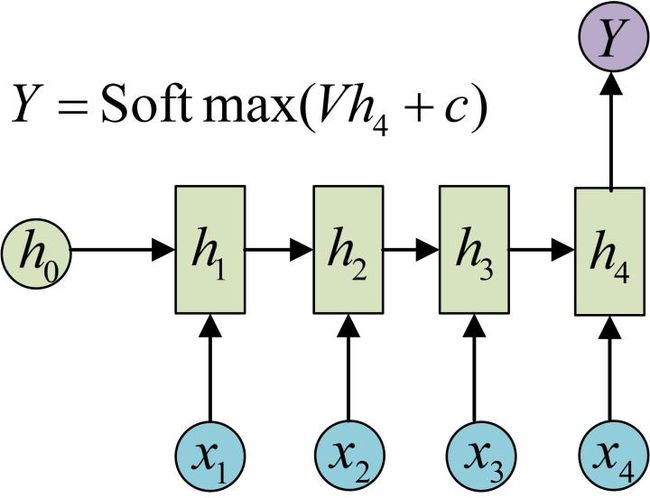
有的时候,我们要处理的问题输入是一个序列,输出是一个单独的值而不是序列,应该怎样建模呢?实际上,我们只在最后一个h上进行输出变换就可以了:
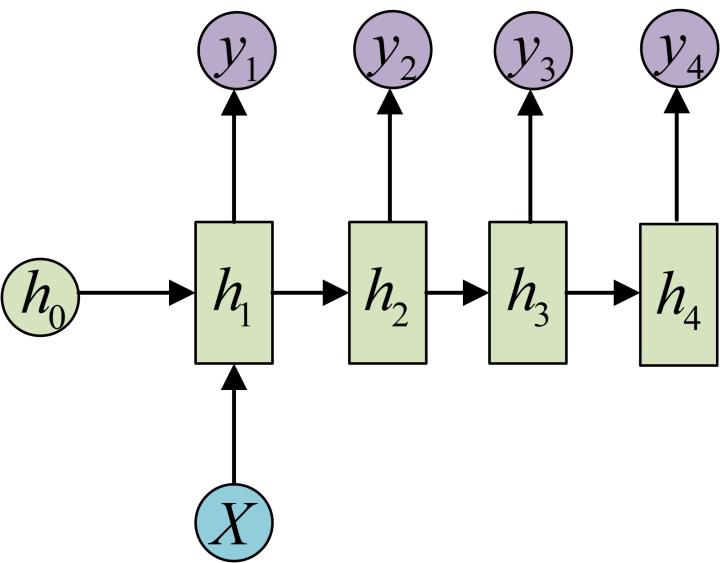
输入不是序列而输出为序列的情况怎么处理?我们可以只在序列开始进行输入计算:
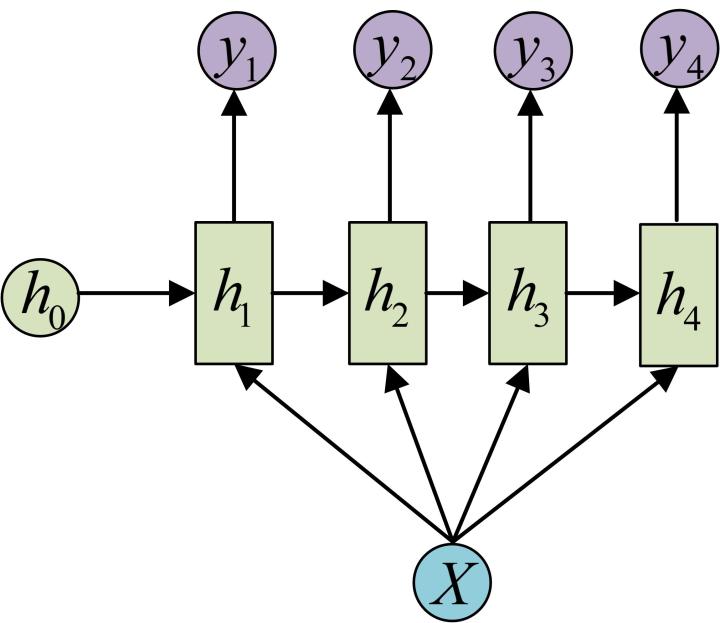
还有一种结构是把输入信息X作为每个阶段的输入:
下图省略了一些X的圆圈,是一个等价表示:
这种1 VS N的结构可以处理的问题有:
- 从图像生成文字(image caption),此时输入的X就是图像的特征,而输出的y序列就是一段句子
- 从类别生成语音或音乐等
下面我们来介绍RNN最重要的一个变种:N vs M。这种结构又叫Encoder-Decoder模型,也可以称之为Seq2Seq模型。
原始的N vs N RNN要求序列等长,然而我们遇到的大部分问题序列都是不等长的,如机器翻译中,源语言和目标语言的句子往往并没有相同的长度。
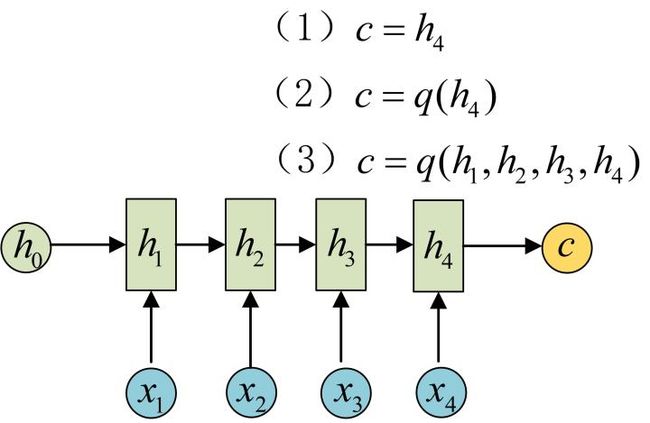
为此,Encoder-Decoder结构先将输入数据编码成一个上下文向量c:
得到c有多种方式,最简单的方法就是把Encoder的最后一个隐状态赋值给c,还可以对最后的隐状态做一个变换得到c,也可以对所有的隐状态做变换。
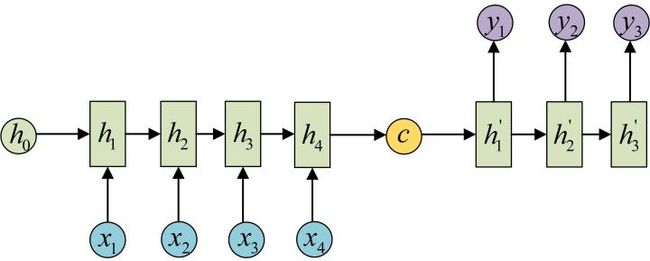
拿到c之后,就用另一个RNN网络对其进行解码,这部分RNN网络被称为Decoder。具体做法就是将c当做之前的初始状态h0输入到Decoder中:
还有一种做法是将c当做每一步的输入:
由于这种Encoder-Decoder结构不限制输入和输出的序列长度,因此应用的范围非常广泛,比如:
- 机器翻译。Encoder-Decoder的最经典应用,事实上这一结构就是在机器翻译领域最先提出的
- 文本摘要。输入是一段文本序列,输出是这段文本序列的摘要序列。
- 阅读理解。将输入的文章和问题分别编码,再对其进行解码得到问题的答案。
- 语音识别。输入是语音信号序列,输出是文字序列。
- …………
seq2seq 的博客还可以看这一篇,讲得很生动形象:https://blog.csdn.net/mmc2015/article/details/72773854
Attention
在Encoder-Decoder结构中,Encoder把所有的输入序列都编码成一个统一的语义特征c再解码,因此, c中必须包含原始序列中的所有信息,它的长度就成了限制模型性能的瓶颈。如机器翻译问题,当要翻译的句子较长时,一个c可能存不下那么多信息,就会造成翻译精度的下降。
Attention机制通过在每个时间输入不同的c来解决这个问题,下图是带有Attention机制的Decoder:
每一个c会自动去选取与当前所要输出的y最合适的上下文信息。具体来说,我们用 衡量Encoder中第j阶段的hj和解码时第i阶段的相关性,最终Decoder中第i阶段的输入的上下文信息 就来自于所有 对 的加权和。
以机器翻译为例(将中文翻译成英文):
输入的序列是“我爱中国”,因此,Encoder中的h1、h2、h3、h4就可以分别看做是“我”、“爱”、“中”、“国”所代表的信息。在翻译成英语时,第一个上下文c1应该和“我”这个字最相关,因此对应的 就比较大,而相应的 、 、 就比较小。c2应该和“爱”最相关,因此对应的 就比较大。最后的c3和h3、h4最相关,因此 、 的值就比较大。
至此,关于Attention模型,我们就只剩最后一个问题了,那就是:这些权重 是怎么来的?
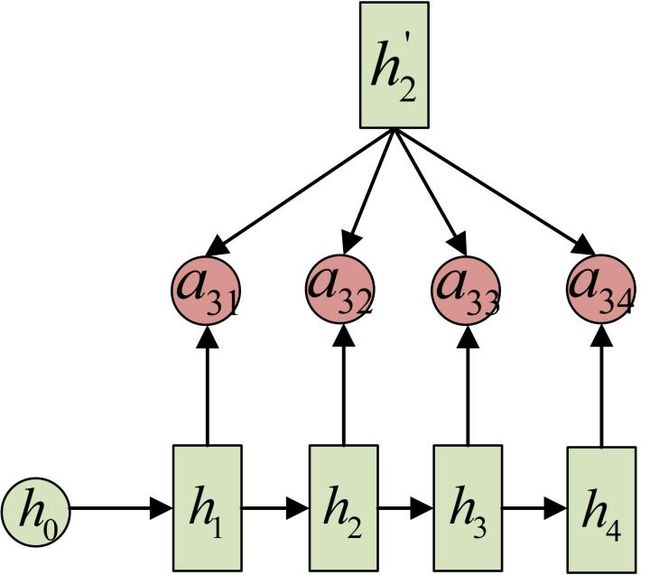
事实上, 同样是从模型中学出的,它实际和Decoder的第i-1阶段的隐状态、Encoder第j个阶段的隐状态有关。
同样还是拿上面的机器翻译举例, 的计算(此时箭头就表示对h'和 同时做变换):
的计算:
的计算:
以上就是带有Attention的Encoder-Decoder模型计算的全过程。
RNN的前向传播算法
RNN的反向传播算法
RNN存在的问题
来自简书: https://www.jianshu.com/p/1a12623f24eb
RNN存在问题:a、梯度消失 ;
b、梯度爆炸;
b、长期依赖问题
梯度消失原因简述:更新模型参数的方法是反向求导,越往前梯度越小。而激活函数是 sigmoid 和 tanh 的时候,这两个函数的导数又是在两端都是无限趋近于0的,会使得之前的梯度也朝向0,最终的结果是到达一定”深度“后,梯度就对模型的更新没有任何贡献。
梯度爆炸原因简述:当参数初始化为足够大,使得tanh函数的倒数乘以W大于1,则将导致偏导极大(大于1的数连乘),从而导致梯度爆炸。
长期依赖问题:相关信息和当前预测位置之间的间隔不断增大时,RNN 会丧失学习到连接如此远的信息的能力。
Eg1:我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词,我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中,相关的信息和预测的词位置之间的间隔是非常小的,RNN 可以学会使用先前的信息。
但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France... I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字,但是如果我们需要弄清楚是什么语言,我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。不幸的是,在这个间隔不断增大时,RNN 会丧失学习到连接如此远的信息的能力。
LSTM的结构
在上节讲的RNN的模型中,RNN的结构如下,每个序列索引位置t都有一个隐藏状态h(t)。
如果我们略去每层都有的o(t),L(t),y(t),则RNN的模型可以简化成如下图的形式:
图中可以很清晰看出隐藏状态h(t)由x(t)和h(t−1)得到。得到h(t)后一方面用于当前层的模型损失计算,另一方面用于计算下一层的h(t+1)。
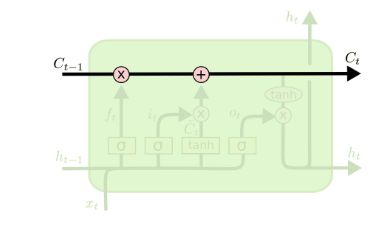
为了解决上述的RNN存在的问题,大牛们对于序列索引位置t的隐藏结构做了改进,可以说通过一些技巧让隐藏结构复杂了起来,来避免梯度消失的问题,这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种,这里我们以最常见的LSTM为例讲述。LSTM的结构如下图:
从上图中可以看出,在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t),还多了另一个隐藏状态,如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State),记为C(t)。如下图所示:
除了细胞状态,LSTM图中还有了很多奇怪的结构,这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门,输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门,输入门和输出门以及细胞状态。
遗忘门
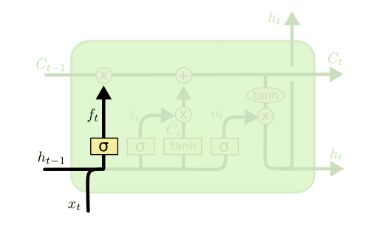
遗忘门(forget gate)顾名思义,是控制是否遗忘的,在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示:
图中输入的有上一序列的隐藏状态h(t−1)和本序列输入数据x(t),通过一个激活函数,一般是sigmoid,得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间,因此这里的输出f(t)代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为:
输入门
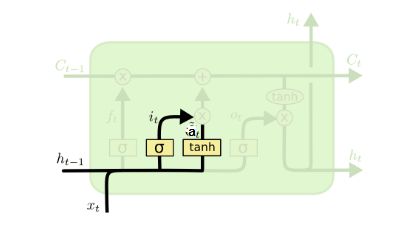
输入门(input gate)负责处理当前序列位置的输入,它的子结构如下图:
从图中可以看到输入门由两部分组成,第一部分使用了sigmoid激活函数,输出为i(t),第二部分使用了tanh激活函数,输出为a(t), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为:
细胞状态更新
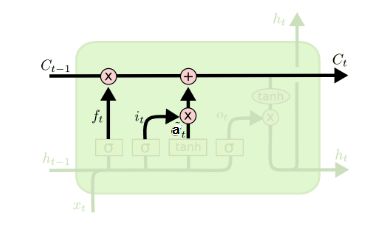
在研究LSTM输出门之前,我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态C(t)。我们来看看从细胞状态C(t−1)如何得到C(t)。如下图所示:
细胞状态C(t)由两部分组成,第一部分是C(t−1)和遗忘门输出f(t)的乘积,第二部分是输入门的i(t)和a(t)的乘积,即:
其中,⊙为Hadamard积,在DNN中也用到过。
输出门
有了新的隐藏细胞状态C(t),我们就可以来看输出门了,子结构如下:
从图中可以看出,隐藏状态h(t)的更新由两部分组成,第一部分是o(t), 它由上一序列的隐藏状态h(t−1)和本序列数据x(t),以及激活函数sigmoid得到,第二部分由隐藏状态C(t)和tanh激活函数组成, 即:
LSTM的前向-反向传播算法
前向传播算法:LSTM模型有两个隐藏状态h(t),C(t),模型参数几乎是RNN的4倍,因为现在多了Wf,Uf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,bo这些参数。
GRU的结构
本节内容来自 https://blog.csdn.net/wangyangzhizhou/article/details/77332582
GRU是LSTM的一个变体,保持了LSTM的效果同时又使结构更加简单,所以它也非常流行。
LSTM有三个门:遗忘门、输入门和输出门,而GRU模型如下,它只有两个门了,分别为更新门和重置门,即图中的zt和rt。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门用于控制忽略前一时刻的状态信息的程度,重置门的值越小说明忽略得越多。
这篇博客讲了GRU每个门的作用,还讲了keras的实现:https://cloud.tencent.com/developer/news/207241
双向LSTM/GRU
在自然语言处理中,因为语法的滞后性,即一个词的修饰词往往在这个词的后面,而普通的RNN网络,只考虑了一个序列中过去的信息对未来的影响,考虑不了这个序列中未来的信息对过去的影响,因此经常用到双向的LSTM/GRU。具体的解析看:https://www.jiqizhixin.com/articles/2018-10-24-13
将词的表示组合成句子的表示,可以采用相加的方法,即将所有词的表示进行加和,或者取平均等方法,但是这些方法没有考虑到词语在句子中前后顺序。如句子“我不觉得他好”。“不”字是对后面“好”的否定,即该句子的情感极性是贬义。使用LSTM模型可以更好的捕捉到较长距离的依赖关系。因为LSTM通过训练过程可以学到记忆哪些信息和遗忘哪些信息。
但是利用LSTM对句子进行建模还存在一个问题:无法编码从后到前的信息。在更细粒度的分类时,如对于强程度的褒义、弱程度的褒义、中性、弱程度的贬义、强程度的贬义的五分类任务需要注意情感词、程度词、否定词之间的交互。举一个例子,“这个餐厅脏得不行,没有隔壁好”,这里的“不行”是对“脏”的程度的一种修饰,通过BiLSTM可以更好的捕捉双向的语义依赖。
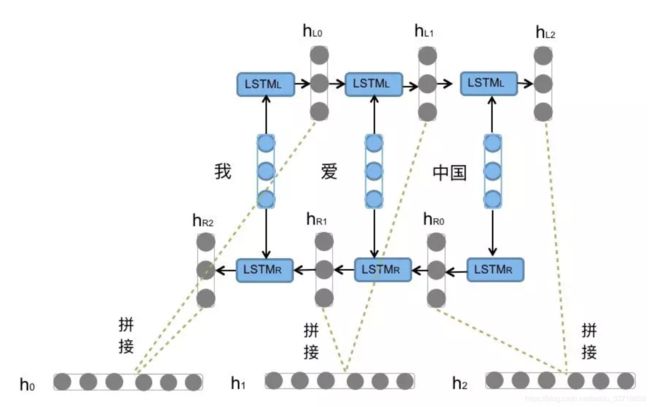
前向的LSTM与后向的LSTM结合成BiLSTM。比如,我们对“我爱中国”这句话进行编码,模型如图所示:
前向的![]() 依次输入“我”,“爱”,“中国”得到三个向量{
依次输入“我”,“爱”,“中国”得到三个向量{![]() ,
, ![]() ,
, ![]() }。后向的
}。后向的![]() 依次输入“中国”,“爱”,“我”得到三个向量{
依次输入“中国”,“爱”,“我”得到三个向量{![]() ,
, ![]() ,
, ![]() }。最后将前向和后向的隐向量进行拼接得到{[
}。最后将前向和后向的隐向量进行拼接得到{[![]() ,
, ![]() ], [
], [![]() ,
, ![]() ], [
], [![]() ,
, ![]() ]},即{
]},即{![]() ,
, ![]() ,
, ![]() }。
}。
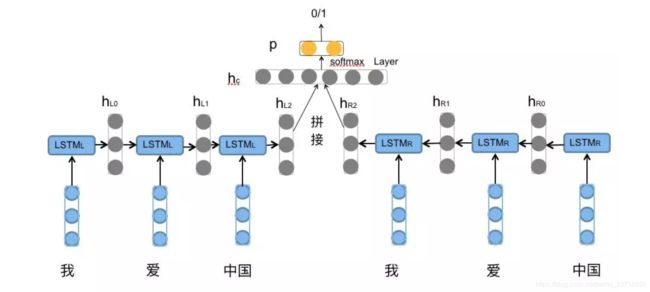
对于情感分类任务来说,我们采用的句子的表示往往是[![]() ,
, ![]() ]。因为其包含了前向与后向的所有信息,如图所示:
]。因为其包含了前向与后向的所有信息,如图所示: