python中利用最小二乘拟合二次抛物线函数

1.最小二乘也可以拟合二次函数

我们都知道用最小二乘拟合线性函数没有问题，那么能不能拟合二次函数甚至更高次的函数呢？答案当然是可以的。下面我们就来试试用最小二乘来拟合抛物线形状的的图像。

对于二次函数来说，一般形状为 f(x) = a*x*x+b*x+c，其中a,b,c为三个我们需要求解的参数。为了确定a、b、c，我们需要根据给定的样本，然后通过调整这些参数，知道最后找出一组参数a、b、c，使这些所有的样本点距离f(x)的距离平方和最小。用什么方法来调整这些参数呢？最常见的自然就是我们的梯度下降喽。

spicy库中有名为leastsq的方法，只需要输入一系列样本点，给出待求函数的基本形状，就可以针对上述问题求解了。

2.抛物线拟合源码

#!/usr/bin/env python
# coding:utf-8


import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq


# 待拟合的数据
X = np.array([1,2,3,4,5,6])
Y=np.array([9.1,18.3,32,47,69.5,94.8])


# 二次函数的标准形式
def func(params, x):
    a, b, c = params
    return a * x * x + b * x + c


# 误差函数，即拟合曲线所求的值与实际值的差
def error(params, x, y):
    return func(params, x) - y


# 对参数求解
def slovePara():
    p0 = [10, 10, 10]

    Para = leastsq(error, p0, args=(X, Y))
    return Para


# 输出最后的结果
def solution():
    Para = slovePara()
    a, b, c = Para[0]
    print "a=",a," b=",b," c=",c
    print "cost:" + str(Para[1])
    print "求解的曲线是:"
    print("y="+str(round(a,2))+"x*x+"+str(round(b,2))+"x+"+str(c))

    plt.figure(figsize=(8,6))
    plt.scatter(X, Y, color="green", label="sample data", linewidth=2)

    #   画拟合直线
    x=np.linspace(0,12,100) ##在0-15直接画100个连续点
    y=a*x*x+b*x+c ##函数式
    plt.plot(x,y,color="red",label="solution line",linewidth=2)
    plt.legend() #绘制图例
    plt.show()


solution()

上面的代码中，稍微注意的是如下几点：
1.func是待拟合的曲线的形状。本例中为二次函数的标准形式。
2.error为误差函数。很多同学会问不应该是最小平方和吗？为什么不是func(params, x) - y * func(params, x) - y？原因是名为lasts的方法中帮我们做了。看一下sklearn中源码的注释就知道什么情况了：

Minimize the sum of squares of a set of equations.
        x = arg min(sum(func(y)**2,axis=0))
                 y

二次方的操作在源码中帮我们实现了。
3.p0里放的是a、b、c的初始值，这个值可以随意指定。往后随着迭代次数增加，a、b、c将会不断变化，使得error函数的值越来越小。
4.leastsq的返回值是一个tuple，它里面有两个元素，第一个元素是a、b、c的求解结果，第二个则为cost function的大小！

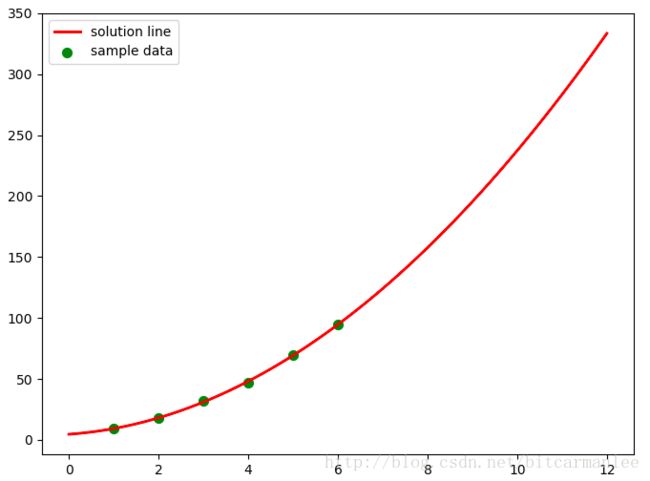
3.程序的最终结果与拟合曲线

程序最终的输出结果：

a= 2.06607141425  b= 2.5975001036  c= 4.68999985496
cost:1
求解的曲线是:
y=2.07x*x+2.6x+4.68999985496

最终的拟合曲线：

4.模拟其他曲线

leastsq函数除了可以模拟线性函数二次函数等多项式，还适用于任何波形的模拟。
比如方波：

def square_wave(x,p):
    a, b, c, T = p
    y = np.where(np.mod(x-b,T)2, 1+c/a, 0)
    y = np.where(np.mod(x-b,T)>T/2, -1+c/a, y)
    return a*y

比如高斯分布：

def gaussian_wave(x,p):
    a, b, c, d= p
    return a*np.exp(-(x-b)**2/(2*c**2))+d

只要将上面代码中的func换成对应的函数即可！