L0范数图像平滑

图像平滑是计算摄影学一门基础重要的工具，其作用是拂去不重要的细节，保留较大的图像边缘，主要应用于边缘检测，JPEG压缩图像人工伪迹去除，非真实绘制等领域。

图像平滑大体上可以分为两类：基于局部和基于全局方法，基于局部的方法像有名 双边滤波， 各向异性扩散，将图像分成一些局部块进行处理；全局方法比如全变分（ Total Variation）和最小二乘滤波( Weighted Least Square)，同时处理整幅图像，可以达到全局最优的目的。
以往的方法，拂去图像中去对图像细节部分也会对图像中大的边缘进行惩罚，这样也会导致图像中大的边缘减弱或丢失，因此徐立等人提出使用图像L0范数平滑，该滤波器是一种基于稀疏策略的全局平滑滤波器。
本文是对香港中文大学徐立等人所做的《Image Smoothing via L0 Gradient Minimization》的读后笔录，也可以看成是论文的翻译吧。使用图像梯度L0范数平滑图像，具有以下优点：

• 通过去除小的非零梯度，抚平不重要的细节信息
• 增强图像显著性边缘

图像梯度L0范数最小化

L0范数可以理解为向量中非零元素的个数。
图像梯度L0范数可以如下表示

c(f):=#{p|∣∣fp−fp−1∣∣≠0}

这里 p 和 p+1 是图像中相邻元素， |fp−fp−1| 就是图像梯度，也即图像的前向差分， #{} 表示计数，输出图像中满足 |fp−fp−1|≠0 的个数，即 c(f) 是图像梯度的L0范数。这样表示有一个优点，就是 c(f) 是非零梯度个数的函数，与图像的梯度本身无关，也就是

#{p|∣∣fp−fp−1∣∣≠0}=#{p|∣∣α(fp−fp−1)∣∣≠0}

这还不是我们的目标函数，只是一个约束条件。

图像梯度最小化平滑

一维信号

先以一维信号为例，输入信号 g ，输出信号 f ，那么我们的目标函数可以如下表示：

minf∑p(fp−gp)2s.t.c(f)=k

左边使得输入信号与输出信号尽可能接近，右边非零约束梯度个数为 k 。下图依次是 k=1,k=2,k=5,k=200 时恢复的信号。

实际上， k 的取值变化范围很大，特别是对于二维图像来说。将上式子转换成无约束问题

minf∑p(fp−gp)2+λ⋅c(f)

这里 λ 是一个权重控制两者之间的比重，实际上它是一个平滑参数，当其值越大越平滑。图像中非零梯度个数与 1λ 呈单调递增关系。
从下图中可以看到梯度 L0 范数的优点，即信号的尖锐部分没有被减弱。

二维图像

二维图像中，我们需要约束图像水平和垂直方向的梯度数目，形式上如下

minf∑p(fp−gp)2+λ⋅c(∂xf,∂yf)

c(∂xf,∂yf)=#{p|∣∣∂xfp∣∣+∣∣∂yfp∣∣≠0}

由于L0范数不可导，全局最优问题是一个NP难问题，所以这里使用变量分裂法，松弛为两个二次规划问题，每个问题都有其闭式解（closed-form）(因为二次函数都可以求导，得到其最小值)。

minf∑p(fp−gp)2+λ⋅c(∂xf,∂yf)+β⋅∑p((∂xfp−hp)2+(∂yfp−vp)2)

迭代优化

• 给定 h，v ，计算 f
  
  E(f)=∑p(fp−gp)2+β⋅((∂xfp−hp)2+(∂yfp−vp)2)
  
  对上式求解，结果取傅里叶变换，可得
  
  f=F−1(F(g)+β(F(∂x)∗F(h)+F(∂y)∗F(v))F(1)+β(F(∂x)∗F(∂x)+F(∂y)∗F(∂y))
  
  本应该ℱ是傅里叶变换专用符号，但这里不支持，因此用了大写 F 。
• 给定 f ，计算 h，v
  
  E(h,v)=∑p((∂xfp−hp)2+(∂yfp−vp)2)+λβc(h,v)
  
  c(h,v) 是 |h|+|v| 中非零元素的个数
  
  E(h,v)=∑p((∂xfp−hp)2+(∂yfp−vp)2)+λβH(|hp|+|vp|)
  
  这里 H(|hp|+|vp|) 是一个二值函数，如果 |hp|+|vp|≠0 返回1，否则0。对于每一个像素来说，有下式
  
  Ep={(∂xfp−hp)2+(∂yfp−vp)2+λβH(|hp|+|vp|)}
  
  上式取得最小值时，得到
  
  hp,vp={(0,0)(∂xSp,∂ySp)(∂xSp)2+(∂ySp)2≤λ/βotherwise
  
  这个证明比较简单，详细推到可以看论文。

代码

%   Distribution code Version 1.0 -- 09/23/2011 by Jiaya Jia Copyright 2011, The Chinese University of Hong Kong.
%
%   The Code is created based on the method described in the following paper 
%   [1] "Image Smoothing via L0 Gradient Minimization", Li Xu, Cewu Lu, Yi Xu, Jiaya Jia, ACM Transactions on Graphics, 
%   (SIGGRAPH Asia 2011), 2011. 
%  
%   The code and the algorithm are for non-comercial use only.


function S = L0Smoothing(Im, lambda, kappa)
%L0Smooth - Image Smoothing via L0 Gradient Minimization
%   S = L0Smooth(Im, lambda, kappa) performs L0 graidient smoothing of input
%   image Im, with smoothness weight lambda and rate kappa.
%
%   Paras: 
%   @Im    : Input UINT8 image, both grayscale and color images are acceptable.
%   @lambda: Smoothing parameter controlling the degree of smooth. (See [1]) 
%            Typically it is within the range [1e-3, 1e-1], 2e-2 by default.
%   @kappa : Parameter that controls the rate. (See [1])
%            Small kappa results in more iteratioins and with sharper edges.   
%            We select kappa in (1, 2].    
%            kappa = 2 is suggested for natural images.  
%
%   Example
%   ==========
%   Im  = imread('pflower.jpg');
%   S  = L0Smooth(Im); % Default Parameters (lambda = 2e-2, kappa = 2)
%   figure, imshow(Im), figure, imshow(S);


if ~exist('kappa','var')
    kappa = 2.0;
end
if ~exist('lambda','var')
    lambda = 2e-2;
end
S = im2double(Im);
betamax = 1e5;
fx = [1, -1];
fy = [1; -1];
[N,M,D] = size(Im);
sizeI2D = [N,M];
otfFx = psf2otf(fx,sizeI2D);
otfFy = psf2otf(fy,sizeI2D);
Normin1 = fft2(S);
Denormin2 = abs(otfFx).^2 + abs(otfFy ).^2;
if D>1
    Denormin2 = repmat(Denormin2,[1,1,D]);
end
beta = 2*lambda;
while beta < betamax
    Denormin   = 1 + beta*Denormin2;
    % h-v subproblem
    h = [diff(S,1,2), S(:,1,:) - S(:,end,:)];
    v = [diff(S,1,1); S(1,:,:) - S(end,:,:)];
    if D==1
        t = (h.^2+v.^2)beta;
    else
        t = sum((h.^2+v.^2),3)beta;
        t = repmat(t,[1,1,D]);
    end
    h(t)=0; v(t)=0;
    % S subproblem
    Normin2 = [h(:,end,:) - h(:, 1,:), -diff(h,1,2)];
    Normin2 = Normin2 + [v(end,:,:) - v(1, :,:); -diff(v,1,1)];
    FS = (Normin1 + beta*fft2(Normin2))./Denormin;
    S = real(ifft2(FS));
    beta = beta*kappa;
    fprintf('.');
end
fprintf('\n');
end

代码也是非常清晰，容易理解的。关于其更多应用，可以查看原文。但是该方法基于迭代优化，迭代次数与kappa对数下降关系， kappa=0.02 迭代22次。

可执行程序

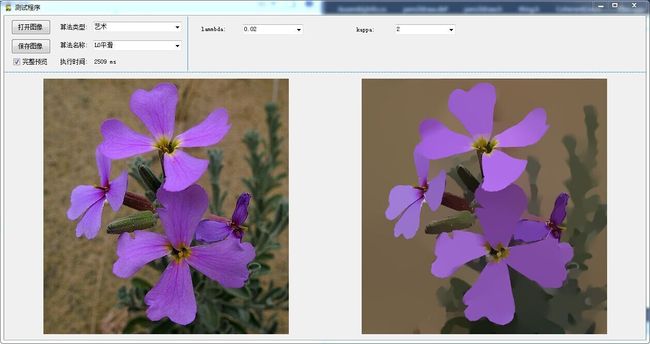
点此可下载exe程序，基于OpenCV编写，仅供学习交流。
界面框架致谢： 人在旅途

参考文献

Image Smoothing via L0 Gradient Minimization
Image Smoothing via L0 Gradient Minimization PPT

Licenses

作者	日期	联系方式
风吹夏天	2015年9月26日	[email protected]