题解-美团点评2017秋招笔试编程题
原题链接:https://www.nowcoder.com/test/5583018/summary
顺序从第四题开始写到第一题
第四题
给出两个字符串(可能包含空格),找出其中最长的公共连续子串,输出其长度。
输入描述:
输入为两行字符串(可能包含空格),长度均小于等于50.
输出描述:
输出为一个整数,表示最长公共连续子串的长度。
示例1
输入
abcde abgde
输出
2
分析:
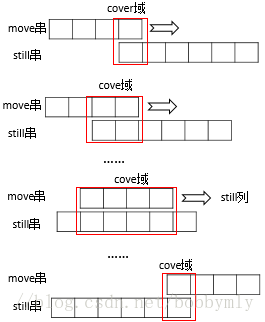
枚举各种长度的各种情况肯定是要超时的
那么就要减少对比的次数,即用尽量少的次数比较出结果
两个字符串滑动一次就是所有可能出现的匹配情况
最大的匹配子串一定在中间的某一次cover域里
而每一次的cover域里我们只需要一个指针滑动一次就能的到最大的匹配长度
完整代码
#include
#include
using namespace std;
int main()
{
string a,b;
getline(cin,a);
getline(cin,b);
int ans=0,lena=a.size(),lenb=b.size(),i,j;
for(i=-lenb;i --------------------------------------------------------------------------------------------------
第三题
输入描述:
输入包括两行,第一行包含一个整数n(1 ≤ n ≤ 10000) 第二行包括n个整数,表示h数组中的每个值,h_i(1 ≤ h_i ≤ 1,000,000)
输出描述:
输出一个整数,表示最大的矩阵面积。
示例1
输入
6 2 1 5 6 2 3
输出
10
分析:
区间面积=区间最小值*区间长度
然后要避免重复求区间最小值即可
每一次遍历中可以从上一个区间的最小值和这一个位置的值更新出新的区间的最小值
即 区间(i,j)的最小值=min(区间(i,j-1)的最小值,j)
这样遍历一次就可以把以 i 为初始位置的所有区间最小值算出,并得到面积,更新结果。
完整代码
#include
#include
#include
#include
using namespace std;
int hight[10005];
int main()
{
int n;
cin>>n;
int ans=0;
for(int i=0;i>hight[i];
for(int i=0;i --------------------------------------------------------------------------------------------------
第二题
给你六种面额 1、5、10、20、50、100 元的纸币,假设每种币值的数量都足够多,编写程序求组成N元(N为0~10000的非负整数)的不同组合的个数。
输入描述:
输入包括一个整数n(1 ≤ n ≤ 10000)
输出描述:
输出一个整数,表示不同的组合方案数
示例1
输入
1
输出
1
分析:
动态规划
对于各种数量的钱,例如 8 可以由 7+1 得到,也可以由 3+5 得到
那么 得到 8 的方法总数 = 得到 7 的方法数+得到 3 的方法数
完整代码
#include
#include
using namespace std;
long long times[10005];
int money[]={1,5,10,20,50,100};
int main()
{
int n;
cin>>n;
times[0]=1;
for(int i=0;i<6;++i)
{
for(int j=money[i];j<=n;++j)
{
times[j]+=times[j-money[i]];
}
}
cout< --------------------------------------------------------------------------------------------------
第一题
大富翁游戏,玩家根据骰子的点数决定走的步数,即骰子点数为1时可以走一步,点数为2时可以走两步,点数为n时可以走n步。求玩家走到第n步(n<=骰子最大点数且是方法的唯一入参)时,总共有多少种投骰子的方法。
输入描述:
输入包括一个整数n,(1 ≤ n ≤ 6)
输出描述:
输出一个整数,表示投骰子的方法
示例1
输入
6
输出
32
分析:
这题较简单
方法很多,要走到 n 位置,每次可以走 n 以内的任意步数
也就说任意位置都可以一步走到终点
所以到达任意位置的方法总数 = 它之前所有位置的方法总数 (因为都可以一步走到我这)+1 (从起点直接一步走到)
在经过简单的数学统计 ans = pow(2,n-1)
完整代码
#include
#include
using namespace std;
int main()
{
int n;
cin>>n;
cout<