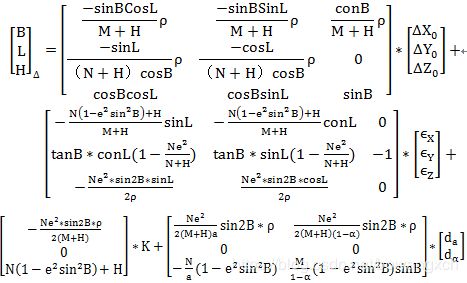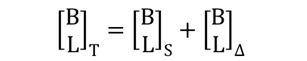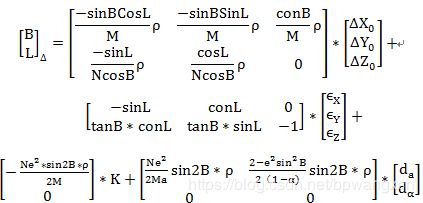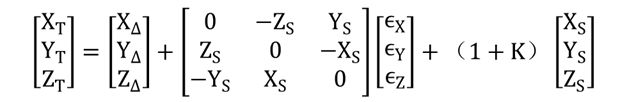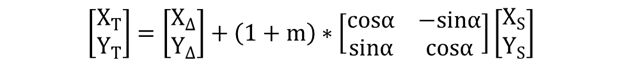坐标系转换相关基本理论

 

理论介绍

大地坐标系与空间直角坐标系的关系

大地坐标系

    是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用大地经度（B）、大地纬度（L）和大地高度（H）表示。

空间直角坐标系

    过空间定点O作三条互相垂直的数轴，它们都以O为原点，具有相同的单位长度·这三条数轴分别称为X轴（横轴）.Y轴（纵轴）.Z轴（竖轴）,统称为坐标轴。

空间直角坐标系是由大地坐标系经过地图投影转换而来。

在我国地图投影采用高斯-克吕格投影投影，简称高斯投影。

高斯投影

高斯-克吕格投影是等角横切椭圆柱投影，由德国数学家高斯提出，后经克吕格扩充并推倒出计算公式，故称为高斯-克吕格投影，简称高斯投影。该投影以中央经线和赤道投影后为坐标轴，中央经线和赤道交点为坐标原点，纵坐标由坐标原点向北为正，向南为负，规定为X轴，横坐标从中央经线起算，向东为正，向西为负，规定为Y轴。所以，高斯-克吕格坐标系的X、Y轴正好对LongruanGIS坐标系和AUTOCAD坐标系的Y和X。

高斯投影的规律：

    (1) 中央子午线的投影为一条直线，且投影之后的长度无变形；其余子午线的投影均为凹向中央子午线的曲线，且以中央子午线为对称轴，离对称轴越远，其长度变形也就越大，变形最大之处在投影带内赤道的两端。

    (2) 赤道的投影为直线，其余纬线的投影为凸向赤道的曲线，并以赤道为对称轴；

    (3) 经纬线投影后仍保持相互正交的关系，即投影后无角度变形；

    (4)  中央子午线和赤道的投影相互垂直。

高斯投影与我国国家坐标系的关系

地球上的点获取的数据起始时用大地坐标系表示的，即用经纬度和高程表示。地球上的数据要在地图上显示出来，就需要将经纬度转化为平面坐标，也就是通常说的x,y坐标。

 

我国地形图一般采用高斯投影，所以通常转化成高斯平面坐标显示到地图上。在经纬度向平面坐标转化的过程中，需要用到椭球参数，因此要考虑所选的坐标系。

 

即（B、L、H）（X、Y、Z）

 

我国常用的坐标系有北京54，西安80等，不同的坐标系对应的椭球体是不一样的。北京54坐标系采用的是克拉索夫斯基椭球体，而西安80采用的是IAG 75地球椭球体。

度带划分

按一定经差将地球椭球面划分成若干投影带, 是高斯投影中限制长度变形的最有效方法。

投影带：以中央子午线为轴，两边对称划出一定区域作为投影范围。

投影带分带原则：

（1）限制长度变形使其不大于测图误差；

（2）带数不应过多以减少换带计算工作。

据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。

通常按经差6度或3度分为六度带或三度带。

六度带自格林威治零度经线起，每6度分为一个投影带，自西向东分带，全球共分为60个投影带，带号依次编为第 1、2…60带。我国6°带中央子午线的经度，由73°起每隔6°而至135°，共计11带，带号用n表示，中央子午线的经度用Ｌ０表示。

 带号及中央子午线经度的关系：

λ ＝６ｎ－３；N=L/6的整数商+1（有余数时候）

注：λ——中央子午线经度； L——点经度； N——投影带号

如，位于东经117 °，因此，在六度带划分时候带号N为20。

 

三度带是在六度带的基础上分成的，它的中央子午线与六度带的中央子午线和分带子午线重合，即自 1.5度子午线起每隔经差3度自西向东分带，带号依次编为三度带第 1、2…120带。中央子午线经度依次为3°, 6°, 9°, … , 360°。

带号及中央子午线经度的关系：

λ ＝3ｎ；n=L/3(四舍五入)

注：λ——中央子午线经度； L——点经度； N——投影带号

如，位于东经117 °，因此，在三度带划分时候带号N为39。

例：某控制点 P 点

按6°带：

按3°带：

    在投影面上，中央子午线和赤道的投影都是直线，并且以中央子午线和赤道的交点O作为坐标原点，以中央子午线的投影为纵坐标轴，以赤道的投影为横坐标轴。

换带计算

在高斯平面直角坐标系中，由于分带投影，使参考椭圆体上统一的坐标系被分割成各带独立的直角坐标系。在生产实践中，有时控制网中的已知点会处于两个投影带中，因而，必须先将邻带的坐标换算为同一带的坐标才能进行检核，这项工作简称坐标换带。

它包括6°带与6°带的坐标互换、6°带与3°带的坐标互换等。

3°带的中央子午线中，有半数与6°带的中央子午线重合。所以，由6°带到3°带的换算区分为2种情况：

① 3°带与6°带的中央子午线重合。

中央子午线一致，坐标系统也就一致，这种情况下，6°带与3°带之间，不存在换带计算问题。如，3°带第39带与6°第20带的中央子午线重合，同为经度117 °。

② 3°带中央子午线与6°带分带子午线不重合

中央子午线不同，坐标系统不一致，必须进行换带计算。

换带计算目前广泛采用高斯投影坐标正反算方法

首先将某投影带的已知平面坐标(x1,y1 )，按高斯投影坐标反算公式求得其大地坐标（B,L）；然后根据纬度B和对于所选定的中央子午线的经差            ，按高斯投影坐标正算公式求其在选定的投影带的平面坐标（x2,y2）。

坐标值类型

在我国x坐标都是正的，y坐标的最大值(在赤道上)约为330km。为了避免出现负的横坐标，则无论3°或6°带，每带的纵坐标轴要西移500 km，即在每带的横坐标上加500 km。

为了指明该点属于何带，还规定在横坐标y值之前，要写上带号。

因此坐标值表现形式有三种：自然值、+500KM值、通用值。

自  然  值：未加500km和带号的横坐标值

加500km值：自然值加500KM不带带号的坐标值

通  用 值：加上500km和带号的横坐标值

自然值：Y1 = +36210.140m, Y2 = -41613.070m

加500Km值： Y1=536210.140m,Y2=458386.930m

通用值：Y1=38 536210.140m,Y2=38 458386.930m

自然值和通用值之间：X不加500km，也不加带号。

我国国家坐标系

1954年北京坐标系

       建国初期，为了迅速开展我国的测绘事业，鉴于当时的实际情况，将我国一等锁与原苏联远东一等锁相连接，然后以连接处呼玛、吉拉宁、东宁基线网扩大边端点的原苏联1942年普尔科沃坐标系的坐标为起算数据，平差我国东北及东部区一等锁，这样传算过来的坐标系就定名为1954年北京坐标系。因此，1954年北京坐标系可归结为：
　　a．属参心大地坐标系；
　　b．采用克拉索夫斯基椭球的两个几何参数；
　　c.  大地原点在原苏联的普尔科沃；
　　d．高程基准为 1956年青岛验潮站求出的黄海平均海水面；
　　e．分区分期局部平差。

 存在问题:

（1）椭球参数有较大误差。

（2）参考椭球面与我国大地水准面存在着自西向东明显的系统性倾斜。

（3）几何大地测量和物理大地测量应用的参考面不统一。

（4）定向不明确。

1980西安坐标系

       1980西安坐标系是为了进行全国天文大地网整体平差而建立的。根据椭球定位的基本原理，在建立C80坐标系时有以下先决条件：

   a．属参心大地坐标系；
   c ．大地原点在我国中部，具体地点是陕西省径阳县永乐镇；
   b．椭球参数采用IUG 1975年大会推荐的参数;
   d ．大地高程以1956年青岛验潮站求出的黄海平均水面为基准;

   e ．天文大地网整体平差.

特点:

（1）椭球面同似大地水准面在我国境内最为密合，是多点定位。

（2）定向明确。

新1954年北京坐标系

   

新1954年北京坐标系（BJ54新）是由1980年国家大地坐标系（GDZ80）转换得来的.

   a．属参心大地坐标系；
   c ．大地原点在我国中部，具体地点是陕西省径阳县永乐镇；
   b．椭球参数采用克拉索夫斯基椭球;
   d ．大地高程以1956年青岛验潮站求出的黄海平均水面为基准;

    e ．天文大地网整体平差.

特点;

（1）是综合GDZ80和BJ54旧 建立起来的参心坐标系。

（2）采用多点定位。但椭球面与大地水准面在我国境内不是最佳拟合。

（4）定向明确。

（5）大地原点与GDZ80相同，但大地起算数据不同。

（6）与BJ54旧 相比，所采用的椭球参数相同，其定位相近，但定向不同。

（7） BJ54旧 与BJ54新 无全国统一的转换参数，只能进行局部转换。

2000国家大地坐标系

2000国家大地坐标系是全球地心坐标系在我国的具体体现，其原点为包括海洋和大气的整个地球的质量中心.

   a．属地心大地坐标系；
   c ．原点为地球的质心；
   b．椭球参数采用WGS84.

       目前利用空间技术所得到的定位和影像等成果，都是以地心坐标系为参照系。

        采用地心坐标系可以充分利用现代最新科技成果，应用现代空间技术进行测绘和定位，快速、精确地获取目标的三维地心坐标，有效提高测量精度和工作效率，为有关部门提供有力的技术支撑。

名词解释

参心坐标系:参心坐标系是以参考椭球的几何中心为基准的大地坐标系.

通常分为：参心空间直角坐标系（以x，y，z为其坐标元素）和参心大地坐标系（以B，L，H为其坐标元素）。

地心坐标系:以地球质心(总椭球的几何中心)为原点的大地坐标系。通常分为地心空间直角坐标系(以x，y，z为其坐标元素)和地心大地坐标系(以B，L，H为其坐标元素)

坐标系转换

坐标转换

坐标转换是空间实体的位置描述，是从一种坐标系统变换到另一种坐标系统的过程。通过建立两个坐标系统之间一一对应关系来实现。

坐标转换分类：

1、大地坐标（BLH）对空间直角坐标（XYZ）；

2、空间直角坐标系间的转换。

实现坐标转换的要素：

1、转换模型；

2、重合点；

3、转换参数。

转换模型

坐标转换模型（1）：

使用条件：已知重合点在两套坐标系下的三维大地坐标

基于大地坐标系的布尔莎三维七参数模型

坐标转换模型（2）

适用条件：是转换模型(1)在大地高H 为零的椭球面上的大地坐标系的简化式

基于大地坐标系的布尔莎二维七参数模型

.

坐标转换模型（3）

适用条件：知道测区内两个坐标系的空间直角坐标值时，可以选择空间直角坐标系的布尔莎七参数模型

基于空间直角坐标系的布尔莎七参数模型

坐标转换模型（4）

适用条件：两维坐标转换，对于三维坐标，需将坐标通过高斯投影变换得到平面坐标再计算转换参数

基于平面直角坐标系的布尔莎四参数模型

重合点

坐标转换重合点选择一般要求：

1、四参数模型重合点不少于2个、七参数模型重合点不少于3个、重合点尽量多选。

2、重合点要覆盖整个转换区域。

3、重合点要均匀分布。

转换控制点：

1、由测绘单位根据各矿井或测区实际控制点情况，对各测区开展D级和E级控制网网形设计。

2、控制点观测方法采用静态测量，并与周围高等级国家连续运行基准站相联测；观测时段采用高等级观测要求，时段长度≥45min，其技术要求按国家标准执行。

3、观测数据进行预处理，与周围高等级国家连续运行基准站联合平差，地心坐标经椭球投影得到大地坐标和平面直角坐标。

4、控制点成果提供包括1954年北京坐标系和1980西安坐标系二套不同的平面成果。

转换流程

坐标系转换的一般流程