Redis源码解析——字典遍历
之前两篇博文讲解了字典库的基础,本文将讲解其遍历操作。之所以将遍历操作独立成一文来讲,是因为其中的内容和之前的基本操作还是有区别的。特别是高级遍历一节介绍的内容,充满了精妙设计的算法智慧。(转载请指明出于breaksoftware的csdn博客)
迭代器遍历
由于Redis字典库有rehash机制,而且是渐进式的,所以迭代器操作可能会通过其他特殊方式来实现,以保证能遍历到所有数据。但是阅读完源码发现,其实这个迭代器是个受限的迭代器,实现方法也很简单。我们先看下其基础结构:
typedef struct dictIterator {
dict *d;
long index;
int table, safe;
dictEntry *entry, *nextEntry;
/* unsafe iterator fingerprint for misuse detection. */
long long fingerprint;
} dictIterator;成员变量d指向迭代器处理的字典。index是dictht中table数组的下标。table是dict结构中dictht数组的下标,即标识ht[0]还是ht[1]。safe字段用于标识该迭代器是否为一个安全的迭代器。如果是,则可以在迭代过程中使用dictDelete、dictFind等方法;如果不是,则只能使用dictNext遍历方法。entry和nextEntry分别指向当前的元素和下一个元素。fingerprint是字典的指纹,我们可以先看下指纹算法的实现:
long long dictFingerprint(dict *d) {
long long integers[6], hash = 0;
int j;
integers[0] = (long) d->ht[0].table;
integers[1] = d->ht[0].size;
integers[2] = d->ht[0].used;
integers[3] = (long) d->ht[1].table;
integers[4] = d->ht[1].size;
integers[5] = d->ht[1].used;
/* We hash N integers by summing every successive integer with the integer
* hashing of the previous sum. Basically:
*
* Result = hash(hash(hash(int1)+int2)+int3) ...
*
* This way the same set of integers in a different order will (likely) hash
* to a different number. */
for (j = 0; j < 6; j++) {
hash += integers[j];
/* For the hashing step we use Tomas Wang's 64 bit integer hash. */
hash = (~hash) + (hash << 21); // hash = (hash << 21) - hash - 1;
hash = hash ^ (hash >> 24);
hash = (hash + (hash << 3)) + (hash << 8); // hash * 265
hash = hash ^ (hash >> 14);
hash = (hash + (hash << 2)) + (hash << 4); // hash * 21
hash = hash ^ (hash >> 28);
hash = hash + (hash << 31);
}
return hash;
} 可以见得,它使用了ht[0]和ht[1]的相关信息进行Hash运算,从而得到该字典的指纹。我们可以发现,如果dictht的table、size和used任意一个有变化,则指纹将被改变。这也就意味着,扩容、锁容、rehash、新增元素和删除元素都会改变指纹(除了修改元素内容)。
生成一个迭代器的方法很简单,该字典库提供了两种方式:
dictIterator *dictGetIterator(dict *d)
{
dictIterator *iter = zmalloc(sizeof(*iter));
iter->d = d;
iter->table = 0;
iter->index = -1;
iter->safe = 0;
iter->entry = NULL;
iter->nextEntry = NULL;
return iter;
}
dictIterator *dictGetSafeIterator(dict *d) {
dictIterator *i = dictGetIterator(d);
i->safe = 1;
return i;
}然后我们看下遍历迭代器的操作。如果是初次迭代,则要查看是否是安全迭代器,如果是安全迭代器则让其对应的字典对象的iterators自增;如果不是则记录当前字典的指纹
dictEntry *dictNext(dictIterator *iter)
{
while (1) {
if (iter->entry == NULL) {
dictht *ht = &iter->d->ht[iter->table];
if (iter->index == -1 && iter->table == 0) {
if (iter->safe)
iter->d->iterators++;
else
iter->fingerprint = dictFingerprint(iter->d);
}因为要遍历的时候,字典可以已经处于rehash的中间状态,所以还要遍历ht[1]中的元素
iter->index++;
if (iter->index >= (long) ht->size) {
if (dictIsRehashing(iter->d) && iter->table == 0) {
iter->table++;
iter->index = 0;
ht = &iter->d->ht[1];
} else {
break;
}
}
iter->entry = ht->table[iter->index];
} else {
iter->entry = iter->nextEntry;
}往往使用迭代器获得元素后,会让字典删除这个元素,这个时候就无法通过迭代器获取下一个元素了,于是作者设计了nextEntry来记录当前对象的下一个对象指针
if (iter->entry) {
/* We need to save the 'next' here, the iterator user
* may delete the entry we are returning. */
iter->nextEntry = iter->entry->next;
return iter->entry;
}
}
return NULL;
}遍历完成后,要调用下面方法释放迭代器。需要注意的是,如果是安全迭代器,就需要让其指向的字典的iterators自减以还原;如果不是,则需要检测前后字典的指纹是否一致
void dictReleaseIterator(dictIterator *iter)
{
if (!(iter->index == -1 && iter->table == 0)) {
if (iter->safe)
iter->d->iterators--;
else
assert(iter->fingerprint == dictFingerprint(iter->d));
}
zfree(iter);
}最后我们探讨下什么是安全迭代器。源码中我们看到如果safe为1,则让字典iterators自增,这样dict字典库中的操作就不会触发rehash渐进,从而在一定程度上(消除rehash影响,但是无法阻止用户删除元素)保证了字典结构的稳定。如果不是安全迭代器,则只能使用dictNext方法遍历元素,而像获取元素值的dictFetchValue方法都不能调用。因为dictFetchValue底层会调用_dictRehashStep让字典结构发生改变。
static void _dictRehashStep(dict *d) {
if (d->iterators == 0) dictRehash(d,1);
}但是作者在源码说明中说安全迭代器在迭代过程中可以使用dictAdd方法,但是我觉得这个说法是错误的。因为dictAdd方法插入的元素可能在当前遍历的对象之前,这样就在之后的遍历中无法遍历到;也可能在当前遍历的对象之后,这样就在之后的遍历中可以遍历到。这样一种动作,两种可能结果的方式肯定是有问题的。我查了下该库在Redis中的应用,遍历操作不是为了获取值就是为了删除值,而没有增加元素的操作,如
void clusterBlacklistCleanup(void) {
dictIterator *di;
dictEntry *de;
di = dictGetSafeIterator(server.cluster->nodes_black_list);
while((de = dictNext(di)) != NULL) {
int64_t expire = dictGetUnsignedIntegerVal(de);
if (expire < server.unixtime)
dictDelete(server.cluster->nodes_black_list,dictGetKey(de));
}
dictReleaseIterator(di);
}高级遍历
高级遍历允许ht[0]和ht[1]之间数据在迁移过程中进行遍历,通过相应的算法可以保证所有的元素都可以被遍历到。我们先看下功能的实现:
unsigned long dictScan(dict *d,
unsigned long v,
dictScanFunction *fn,
void *privdata)参数d是字典的指针;v是迭代器,这个迭代器初始值为0,每次调用dictScan都会返回一个新的迭代器。于是下次调用这个函数时要传入新的迭代器的值。fn是个函数指针,每遍历到一个元素时,都是用该函数对元素进行操作。
typedef void (dictScanFunction)(void *privdata, const dictEntry *de);Redis中这个方法的调用样例是:
do {
cursor = dictScan(ht, cursor, scanCallback, privdata);
} while (cursor &&
maxiterations-- &&
listLength(keys) < (unsigned long)count);对于不在rehash状态的字典,则只要对ht[0]中迭代器指向的链表进行遍历就行了
dictht *t0, *t1;
const dictEntry *de;
unsigned long m0, m1;
if (dictSize(d) == 0) return 0;
if (!dictIsRehashing(d)) {
t0 = &(d->ht[0]);
m0 = t0->sizemask;
/* Emit entries at cursor */
de = t0->table[v & m0];
while (de) {
fn(privdata, de);
de = de->next;
}
如果在rehash状态,就要遍历ht[0]和ht[1]。遍历前要确定哪个dictht.table长度短(假定其长度为len=8),先对短的中该迭代器(假定为iter=4)对应的链进行遍历,然后遍历大的。然而不仅要遍历大的dictht中迭代器(iter=4)对应的链,还要遍历比iter大len的迭代器(4+8=12)对应的链表。
} else {
t0 = &d->ht[0];
t1 = &d->ht[1];
/* Make sure t0 is the smaller and t1 is the bigger table */
if (t0->size > t1->size) {
t0 = &d->ht[1];
t1 = &d->ht[0];
}
m0 = t0->sizemask;
m1 = t1->sizemask;
/* Emit entries at cursor */
de = t0->table[v & m0];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Iterate over indices in larger table that are the expansion
* of the index pointed to by the cursor in the smaller table */
do {
/* Emit entries at cursor */
de = t1->table[v & m1];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Increment bits not covered by the smaller mask */
v = (((v | m0) + 1) & ~m0) | (v & m0);
/* Continue while bits covered by mask difference is non-zero */
} while (v & (m0 ^ m1));
}最后要重新计算下次使用的迭代器并返回
/* Set unmasked bits so incrementing the reversed cursor
* operates on the masked bits of the smaller table */
v |= ~m0;
/* Increment the reverse cursor */
v = rev(v);
v++;
v = rev(v);
return v;
}从上面的设计来看,调用dictScan时不能有多线程操作该字典,否则会出现遗漏遍历的情况。但是在每次调用dictScan之间可以对字典进行操作。
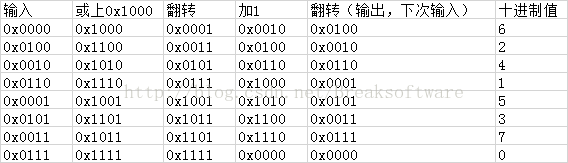
其实这个遍历中最核心的是迭代器v的计算方法,我们只要让v从0开始,执行“或操作”最短ht.table(~m0)大小、二进制翻转、加1、再二进制翻转就可以实现0到~m0的遍历。我们看个例子:
我一直想不出这套算法为什么能满足这样的特点,还是需要数学大神解释一下。同时也可见这种算法的作者Pieter Noordhuis数学有一定功底。
关键这样的算法不仅可以完成遍历,还可以在数组大小动态变化时保证元素被全部遍历到。我把代码提炼出来,模拟了长度为8的数组向长度为16的数组扩容,和长度为16的数组向长度为8的数组缩容的过程。为了让问题简单化,我们先不考虑两个数组的问题,只认为数组在一瞬间被扩容和缩容。
我们先看下扩容前的遍历过程

此时多了一次对下标为15的遍历,可以想象这次遍历应该会重复下标为15%8=7遍历(即第8次)的元素。所以dictScan具有潜在对一个元素遍历多次的问题。我们再看第7次迭代时发生瞬间扩容的情况

此时数组下标为11的遍历(即第8次遍历)会部分重复下标为3的遍历(即第7次遍历)元素。而之后的遍历就不会重复了。
我们再看下数组的缩容。为缩容前的状态是

可见第16次遍历的是新数组下标为7的元素,和第15次遍历老数组下标为7的元素不同,本次遍历的结果包含前者(因为它还包含之前下标为15的元素)。所以也存在元素重复遍历的问题。
我们看下第15次遍历时突然缩容的遍历过程
因为缩容到8,所以最后一次遍历下标7的情况,既包括之前老数组下标为7的元素,也包含老数组下标为15的元素。所以本次遍历不会产生重复遍历元素的问题。
我们再看下第14次遍历突然缩容的遍历过程
第14次本来是要遍历下标为11的元素。由于发生缩容,就遍历新的数组的下标为3的元素。所以第14的遍历包含第13次的遍历元素。
一个数组如此,像dict结构中有两个dictht的情况,则稍微复杂点。我们通过下图可以发现,不同时机ht[0]扩容或者缩容,都可以保证元素被全遍历
上面测试的代码是:
#define TWO_FOUR_MASK 15
#define TWO_THREE_MASK 7
static unsigned long rev(unsigned long v) {
unsigned long s = 8 * sizeof(v);
unsigned long mask = ~0;
while ((s >>= 1) > 0) {
mask ^= (mask <> s) & mask) | ((v << s) & ~mask);
}
return v;
}
unsigned long loop_single_expand_shrinks(unsigned long v, int change, int expand) {
unsigned long m0 = 0;
if (expand) {
if (change) {
m0 = TWO_FOUR_MASK;
}
else {
m0 = TWO_THREE_MASK;
}
}
else {
if (change) {
m0 = TWO_THREE_MASK;
}
else {
m0 = TWO_FOUR_MASK;
}
}
unsigned long t0idx = t0idx = v & m0;
printf(" t0Index: %lu ", t0idx);
v |= ~m0;
v = rev(v);
v++;
v = rev(v);
return v;
}
unsigned long loop(unsigned long v) {
unsigned long m0 = TWO_THREE_MASK;
unsigned long m1 = TWO_FOUR_MASK;
unsigned long t0idx = v & m0;
printf(" t0Index: %lu ", t0idx);
printf(" t1Index: ");
do {
unsigned long t1idx = v & m1;
printf("%lu ", t1idx);
v = (((v | m0) + 1) & ~ m0) | (v & m0);
} while (v & (m0 ^ m1));
v |= ~m0;
v = rev(v);
v++;
v = rev(v);
return v;
}
unsigned long loop_expand_shrinks(unsigned long v, int change, int expand) {
unsigned long m0 = 0;
unsigned long m1 = 0;
if (!change) {
m0 = TWO_THREE_MASK;
m1 = TWO_FOUR_MASK;
unsigned long t0idx = v & m0;
if (expand) {
printf(" t0Index: %lu ", t0idx);
printf(" t1Index: ");
}
else {
printf(" t1Index: %lu ", t0idx);
printf(" t0Index: ");
}
do {
unsigned long t1idx = v & m1;
printf("%lu ", t1idx);
v = (((v | m0) + 1) & ~ m0) | (v & m0);
} while (v & (m0 ^ m1));
}
else {
if (expand) {
m0 = TWO_FOUR_MASK;
}
else {
m0 = TWO_THREE_MASK;
}
unsigned long t0idx = v & m0;
printf(" t0Index: %lu ", t0idx);
}
v |= ~m0;
v = rev(v);
v++;
v = rev(v);
return v;
}
void print_binary(unsigned long v) {
char s[128] = {0};
_itoa_s(v, s, sizeof(s), 2);
printf("0x%032s", s);
}
void check_loop_normal() {
unsigned long v = 0;
do
{
print_binary(v);
v = loop(v);
printf("\n");
} while (v != 0);
}
void check_loop_expand_shrinks(int expand) {
int loop_count = 9;
for (int n = 0; n < loop_count; n++) {
unsigned long v = 0;
int change = 0;
int call_count = 0;
do
{
if (call_count == n) {
change = 1;
}
print_binary(v);
v = loop_expand_shrinks(v, change, expand);
call_count++;
printf("\n");
} while (v != 0);
printf("\n");
}
}
void check_loop_single_expand_shrinks(int expand) {
int loop_count = 17;
for (int n = 0; n < loop_count; n++) {
unsigned long v = 0;
int change = 0;
int call_count = 0;
do
{
if (call_count == n) {
change = 1;
}
print_binary(v);
v = loop_single_expand_shrinks(v, change, expand);
call_count++;
printf("\n");
} while (v != 0);
printf("\n");
}
}