Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics

论文：https://arxiv.org/abs/1705.07115v3

1 问题引出

多任务联合学习可以提升各任务的学习效果，因为多任务可以共享数据集、共享低层特征。但多任务联合学习时，该如何对各子任务的损失函数进行加权才能取得最优的训练效果，这是本文所关心的问题。

本文中作者提出的多任务如下图所示：
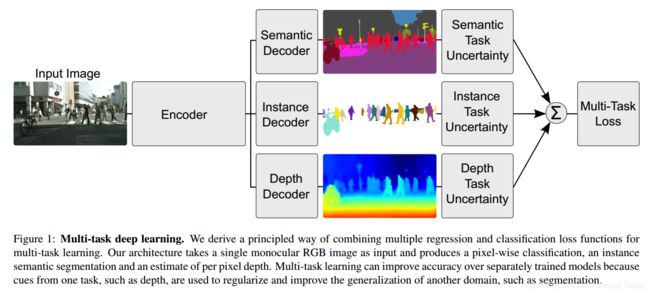对各任务的损失确定加权系数$w_i$可以有多种方式，把这些系数作为超参数进行调试的代价很大，因此作者提出了基于任务的不确定性确定系数。

2 解决方案

在贝叶斯建模中，需要解决两种不同类型的不确定性。

• 认知不确定性：表示的是模型本身的不确定性，这是因为缺乏训练数据，模型认知不足，可以通过扩充训练集进行解决；
• 偶然不确定性：偶然不确定性表示数据不能解释的信息。

偶然不确定性又分成两类：

• 数据依赖(异方差)不确定性：依赖于输入数据的不确定性，体现在模型的输出上；
• 任务依赖(同方差)不确定性：不取决于输入数据，而是取决于不同的任务。

在多任务联合学习中，任务依赖不确定性能够表示不同任务间的相对难度。下面证明了在多任务学习中可以通过通过任务依赖不确定性对不同的损失进行加权。

2.1 多任务似然

下面通过最大化同方差不确定性的最大高斯似然推导多任务损失函数。

假设输入为X，参数矩阵为W，输出为$f^W(x)$。

对于回归任务，定义其概率为以输出为均值的高斯似然，即
$$p(y|f^W(x))=N(f^W(x),{\sigma }^2)\text{\hspace{1em}(2)}$$

对于分类任务，定义：
$$p(y|f^W(x))=Softmax(f^W(x))\text{\hspace{1em}(3)}$$

多任务模型，其似然为：
$$p(y_1,\cdots ,y_k|f^W(x))=p(y_1|f^W(x))\cdots p(y_K|f^W(x))\text{\hspace{1em}(4)}$$

回归任务：

对于回归任务，即公式(2)，其对数似然为：
$$\log p(y|f^W(x))\propto -\frac{1}{2{\sigma }^2}||y-f^W(x)|{|}^2-\log \sigma \text{\hspace{1em}(5)}$$
对于高斯似然，$\sigma$为模型的观测噪声参数，表示输出数据中的噪声量。

我们的目的是基于参数矩阵$W$和标准差$\sigma$最大化对数似然。

假设多任务模型进行两个回归任务，两个任务都符合高斯分布，输出分别是$y_1$和$y_2$，那么总的对数似然为：
$$\begin{gathered} p(y1,y2|f^W(x))=p(y1|f^W(x))p(y2|f^W(x)) \\ =N(y1;f^W(x),{\sigma }_1^2)N(y2;f^W(x),{\sigma }_2^2)\text{\hspace{1em}(6)} \end{gathered}$$

取对数，优化目标变成了最大化对数似然，也是最小化负对数似然，即：
$$\begin{gathered} -\log p(y1,y2|f^W(x)) \\ \propto \frac{1}{2{\sigma }_1^2}||y_1-f^W(x)|{|}^2+\frac{1}{2{\sigma }_2^2}||y_2-f^W(x)|{|}^2+\log {\sigma }_1{\sigma }_2 \\ =\frac{1}{2{\sigma }_1^2}{L}_1(w)+\frac{1}{2{\sigma }_2^2}{L}_2(w)+\log {\sigma }_1{\sigma }_2\text{\hspace{1em}(7)} \end{gathered}$$

要是想最小化负对数似然，就需要调整${\sigma }_1$和${\sigma }_2$的值。${\sigma }_1$增加，$L_1(w)$会减小，反之亦然。最后项影响不大，可以当作正则化项。

分类任务：

对于分类任务的概率，添加一个标量缩放系数${\sigma }^2$。

$$p(y|f^W(x),\sigma )=Softmax(\frac{1}{{\sigma }^2}{f}^W(x))\text{\hspace{1em}(8)}$$

这被称作是Boltzmann分布，也叫做吉布斯分布。系数${\sigma }^2$可以是设定的，也可以是通过学习得到的，决定离散分布的平坦程度。该值和分布的不确定性(熵)有关。其对数似然可以写成：
$$\log p(y=c|f^W(x),\sigma )=\frac{1}{{\sigma }^2}{f}_c^W(x)-\log (\sum _{c^{{}^{\prime }}}\exp (\frac{1}{{\sigma }^2}{f}_{c^{{}^{\prime }}}^W(x)))\text{\hspace{1em}(9)}$$

回归和分类任务：

假设一个多任务模型由一个分类任务和一个回归任务组成，那么联合损失为：

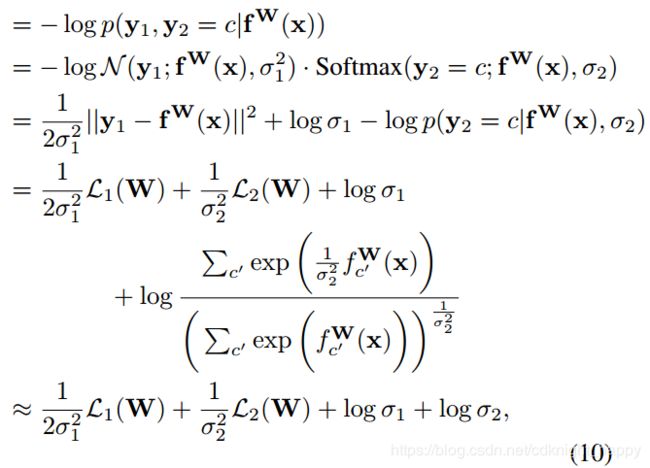
上式中，$L_1(W)=||y_1-f^W(x)|{|}^2$，为回归子任务输出和真实label$y_1$间的欧式距离。$L_2(W)=-\log (Softmax(y_2,f^W(x)))$是分类子任务的交叉熵损失。优化的目的是同时寻找最优的$W$、${\sigma }_1$和${\sigma }_2$。

最终的目标可以看成是学习每一个子任务输出的相对权重。大的${\sigma }_2$会降低$L_2(W)$的影响，小的${\sigma }_2$会增大$L_2(W)$的影响。

作者最终的做法是在模型训练的过程中去优化${\sigma }_1$和${\sigma }_2$，并且为了提升数值稳定性，作者去学习参数$s:=\log {\sigma }^2$。

实验结果：
基于三个任务的不确定性进行损失加权的效果最好。

参考：https://blog.csdn.net/u013453936/article/details/83475590