Bilinear CNNs for Fine-grained Visual Recognition
1 简介
细粒度识别即对隶属于同一类的目标进行分类，包括鸟的物种识别、汽车的型号识别和狗的品种识别。细粒度识别高度依赖目标的局部特征，例如，要将“加利福尼亚鸥”与“环嘴鸥”区分开来，需要识别其喙上的图案或它们羽毛的细微颜色差异。两类技术适合于解决细粒度分类任务。一是基于部件的识别模型，这些模型检测并提取部件的特征进行细粒度的类别区分。另一种方法是基于全局图像的整体模型。基于部件的模型往往更加精确，但由于图像部件标注成本太高，很难获取大规模的数据集，所以这种方法不实用。实际应用种往往更需要仅仅依据图像的类别信息完成细粒度识别任务。
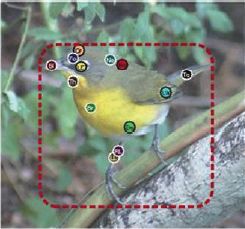
进行了部件标注的目标图像，图像参考自https://blog.csdn.net/qq_16525279/article/details/80415786
在本文中，我们认为基于部件的推理的有效性源于它们对目标的位置和姿势的不变性。纹理表示在设计上是平移不变的，因为它们基于无序方式聚集局部图像特征。虽然传统的SIFT纹理表示和最近的CNN特征表示在细粒度目标分类上也比较有效，但仍然达不到基于部件的方法的分类效果。造成这种差距的一个潜在原因是，纹理表示中的基础特征不是以端到端的方式学习的，因此对于识别任务而言可能不是最佳的。
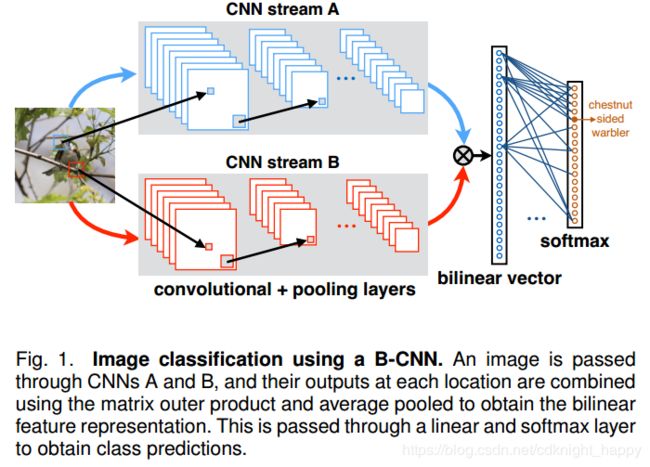
我们提出了双线性CNN（B-CNN），它解决了现有深度纹理表示的几个缺点。我们的主要观点在于，可以将几种广泛使用的纹理表示形式变换为两个经过适当设计的特征集的外积。当使用CNN进行特征提取时，后面使用特殊设计的bilinear层和池化层就可以实现B-CNN。输出的高维特征向量通过全连接层即可预测目标类别。最简单的bilinear层即输入两个相同的特征进行外积操作。我们还发现，一旦将适当的非线性应用于基础特征，其他纹理表示就可以写为B-CNN。这导致了一系列的层，可以将这些层插入现有的CNN中，以对大型数据集进行端到端训练，或者对特定领域进行微调以进行迁移学习。B-CNN在各种细粒度的识别数据集上优于现有模型，包括监督训练的部件模型。而且，这些模型非常高效。我们在MatConvNet [66]中实现的最精确的模型在NVIDIA Titan X GPU上以每秒30帧的速度运行，在Caltech-UCSD鸟类数据集[67]和NABirds [64]，FGVC飞机[42]和Stanford汽车[33]数据集上，图像识别的准确度达到84.1％，79.4％，86.9％和91.3％。
2 用于图像分类的B-CNN
2.1 B-CNN结构
用于图像分类的B-CNN可以表示成 β = ( f A , f B , P , C ) \beta = (f_A,f_B,P,C) β=(fA,fB,P,C)的形式， f A f_A fA和 f B f_B fB表示基于CNN的特征提取函数，P表示池化函数，C是分类函数。 f : L × I → R K × D f:L \times I \rightarrow R^{K \times D} f:L×I→RK×D，输入图像 I I I和位置 L L L，得到大小为 K × D K \times D K×D的输出特征。通过矩阵外积得到每个位置的输出特征，即位置 l l l处的特征 f A f_A fA和 f B f_B fB的双线性结合为：
b i l i n e a r ( l , I , f A , f B ) = f A ( l , I ) T f B ( l , I ) (1) bilinear(l,I,f_A,f_B) = f_A(l,I)^Tf_B(l,I) \tag{1} bilinear(l,I,fA,fB)=fA(l,I)TfB(l,I)(1)
池化函数 P P P的作用是在不同的位置L处的特征进行整合，作者使用的是sum池化，即：
Φ ( I ) = ∑ l ∈ L b i l i n e a r ( l , I , f A , f B ) = ∑ l ∈ L f A ( l , I ) T f B ( l , I ) (2) \Phi(I) = \sum_{l \in L}bilinear(l,I,f_A,f_B)=\sum_{l \in L}f_A(l,I)^Tf_B(l,I) \tag{2} Φ(I)=l∈L∑bilinear(l,I,fA,fB)=l∈L∑fA(l,I)TfB(l,I)(2)
由于在进行池化处理的过程中忽略了特征的位置，因此bilinear特征是一个无序表示。
B-CNN中的特征函数可以不共享/部分共享/完全共享。
2.2 归一化和分类函数
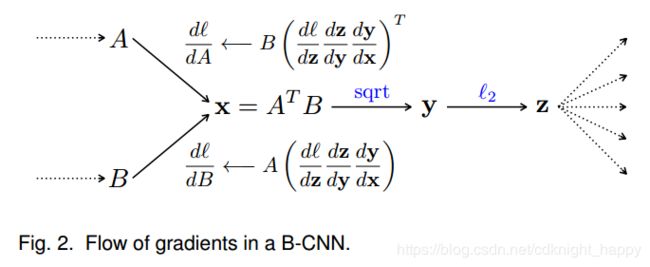
对bilinear特征 x = Φ ( I ) x = \Phi(I) x=Φ(I)求带符号的平方根操作，即 y ← s i g n ( x ) ∣ x ∣ y \leftarrow sign(x)\sqrt{|x|} y←sign(x)∣x∣，然后再进行 l 2 l_2 l2正则化操作， z ← y / ∣ ∣ y ∣ ∣ 2 z \leftarrow y/||y||^2 z←y/∣∣y∣∣2，这样做可以提升模型性能。
分类函数使用logistic regression 或 linear SVM，作者发现线性分类模型对于bilinear特征的分类效果较好。
2.3 端到端训练
B-CNN可以端到端的方式进行训练。
3 实验
细粒度分类有下列四个数据集：
- CUB-200-2011：11788幅图像，200种鸟。除了标注鸟的类别之外，还标注了鸟的局部bounding box用于凸显特征区域；
- FGVC-aircraft：10000幅图像，100种飞机。只标注了飞机的类型信息。
- Stanford cars：16185幅图像，196类汽车。标注了汽车的品牌、型号、年份。
- NABirds：48562幅图像，555种鸟。标注了鸟的类别和局部bounding box信息。
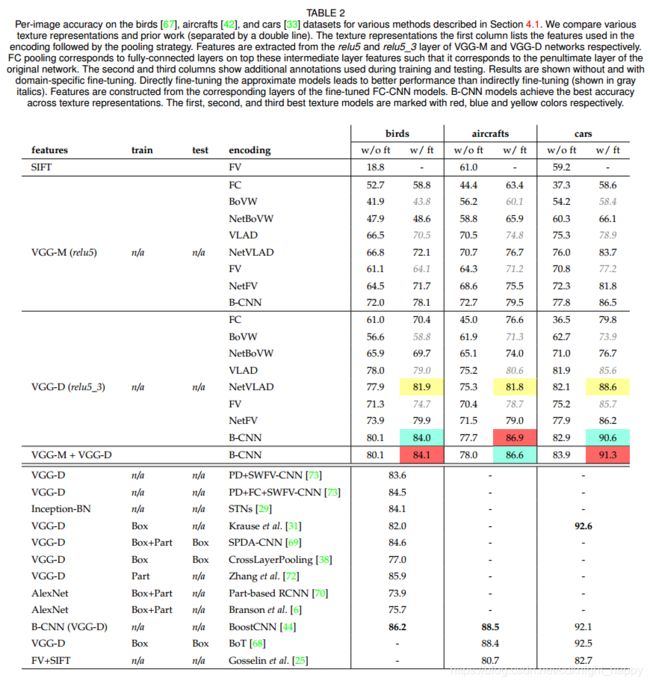使用B-CNN微调的效果较好；
在相近的模型上微调的效果比直接训练的效果好。
4 B-CNN分析
4.1 降维
B-CNN计算了特征的外积，这样原始输出为512维特征的模型经过外积之后的特征变成了 512 × 512 ≈ 262 k 512 \times 512 \approx 262k 512×512≈262k。为了减小计算量，可以采取下述几种降维方法：
- 先外积后降维，即 Φ ( x , y ) = v e c ( x T y ) P \Phi(x,y) = vec(x^Ty)P Φ(x,y)=vec(xTy)P， v e c vec vec操作将外积矩阵变换成向量，P表示降维的映射矩阵；
- 先降维后外积，即 Φ ( x , y ) = ( x A ) T ( x B ) \Phi(x,y)=(xA)^T(xB) Φ(x,y)=(xA)T(xB)，A，B均表示降维映射矩阵；
- 对其中一个特征降维再计算外积，假如对 x x x进行降维处理，则设置B为单位矩阵。
上述三种方法中，降维映射矩阵都可以使用PCA得到。第一种方法比较直观，但是PCA的计算量很大，因为外积的维度为 d 2 d^2 d2，那么其协方差矩阵的维度为 d 4 d^4 d4。第二种方法计算量小，但是准确率损失的太大。实验中发现第三种方法效果最好。降维矩阵使用PCA进行初始化，但其可以参与训练过程。
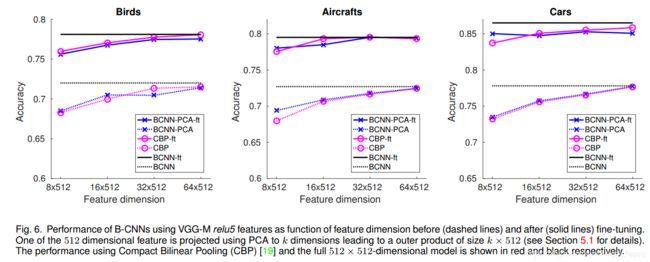
微调比从头训练效果好；
作者提出的第三种降维方式效果最好，超越了PCA降维和CBP(Compact Bilinear Pooling)。
4.2 B-CNN分类原理分析
上图为激活值最大的区域所对应的输入图像块。从上图可以看出，B-CNN能够自动定位具有区分能力的局部块。
下面文字引用自：https://blog.csdn.net/qq_16525279/article/details/80415786
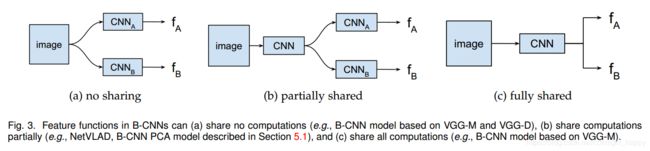
一种对双线性CNN模型的解释是, 网络A的作用是对物体进行定位, 即完成传统算法的对象与局部区域检测工作, 而网络B则是用来对网络A检测到的物体位置进行特征提取. 两个网络相互协调作用, 完成细粒度图像分类过程中两个最重要的任务: 区域检测与特征提取。