Python之Numpy入门实战教程(1):基础篇
Numpy、Pandas、Matplotlib是Python的三个重要科学计算库,今天整理了Numpy的入门实战教程。NumPy是使用Python进行科学计算的基础库。 NumPy以强大的N维数组对象为中心,它还包含有用的线性代数,傅里叶变换和随机数函数。
强烈建议大家将本文中的程序运行一遍。这样能加深对numpy库的使用。
目录
1.Creating arrays
1)创建全零数组
2)创建其余类型数组
2.Array data
3.Reshaping an array
1)reshape and ravel
4.Arithmetic operations
5.Broadcasting
1)广播规则
6.Conditional operators
7.Mathematical and statistical functions
1)ndarray methods
2)Universal functions
3)Binary ufuncs
8.Array indexing
1)Differences with regular python arrays
2)Multi-dimensional arrays
3) Fancy indexing &Higher dimensions&Boolean indexing
9.Iterating
10.Stacking arrays
1)vstack
2)hstack
3)concatenate
4)stack
11.Splitting arrays
12.Transposing arrays
13.Vectorization
14.Saving and loading
1.Creating arrays
1)创建全零数组
]现在我们来导入numpy,并进行创建数组操作:
#导入numpy库
import numpy as np
np.zeros(5) #输出 “array([0., 0., 0., 0., 0.])”
#创建二维数组,并指定行数和列数
np.zeros(3,4)
#输出
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
下面来介绍一下,在numpy中有关的概念:
- axis:在numpy中,每一个维度称为axis;
- rank:轴的个数称为rank;例如:上面的3x4矩阵的秩为2,;
- shape:一个维度上的列表长度称为shape;例如:上面的矩阵的shape是(3, 4);
- size:数学的所有元素个数为size;例如:上面矩阵的size是:3*4=12;
a = np.zeros((3,4))
a
#输出
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
a.shape #输出 "(3,4)"
a.ndim #相当于len(a.shape) 输出"2"
a.size #输出 "12"
我们现在来创建任意维度的数组,下面是创建一个3维数组,形状是(2,3,4):
np.zeros((2,3,4))
#输出
array([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]])
#查看数组类型
type(np.zeros((3,4))) #输出 "numpy.ndarray"
2)创建其余类型数组
#创建元素全为1的数组
np.ones(1)
#输出
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
#创建给定值初始化的数组,这是一个全为π的3x4矩阵
np.full((3,4), np.pi)
#输出
array([[3.14159265, 3.14159265, 3.14159265, 3.14159265],
[3.14159265, 3.14159265, 3.14159265, 3.14159265],
[3.14159265, 3.14159265, 3.14159265, 3.14159265]])
#一个未初始化的2x3数组(内容随机)
np.empty((2,3))
#输出
array([[4.65802320e-310, 4.65802160e-310, 4.65802012e-310],
[6.94949919e-310, 0.00000000e+000, 0.00000000e+000]])
#使用array函数和常规python数组初始化ndarray
np.array([[1,2,3,4], [10,20,30,40]])
#输出
array([[ 1, 2, 3, 4],
[10, 20, 30, 40]])
#使用NumPy的范围函数创建一个ndarray,它类似于python的内置范围函数
np.arange(1, 5) #输出 array([1, 2, 3, 4])
np.arange(1.0, 5.0) #输出 array([1., 2., 3., 4.])
#提供步长参数
np.arange(1, 5, 0.5) #输出 array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5])
#当元素为浮点数时,元素个数可能会有变化
print(np.arange(0, 5/3, 1/3))
print(np.arange(0, 5/3, 0.333333333))
print(np.arange(0, 5/3, 0.333333334))
#输出
[0. 0.33333333 0.66666667 1. 1.33333333 1.66666667]
[0. 0.33333333 0.66666667 1. 1.33333333 1.66666667]
[0. 0.33333333 0.66666667 1. 1.33333334]
#在使用浮点数时,通常最好使用linspace函数而不是arange
print(np.linspace(0, 5/3, 6))
#输出
[0. 0.33333333 0.66666667 1. 1.33333333 1.66666667]
#NumPy的随机模块中提供了许多函数来创建用随机值初始化的ndarray(0-1之间)
np.random.rand(3,4)
#输出
array([[0.7277128 , 0.68775769, 0.34351181, 0.02168851],
[0.86629136, 0.06427389, 0.64314693, 0.94817528],
[0.21333456, 0.78559298, 0.71692429, 0.5635313 ]])
#随机初始化矩阵,服从高斯分布(均值为0,方差为1)
np.random.randn(3,4)
#输出
array([[-1.07334865, 1.57525255, -0.07676677, 0.95149926],
[ 0.9378264 , -1.20141156, 0.08230785, 0.38547522],
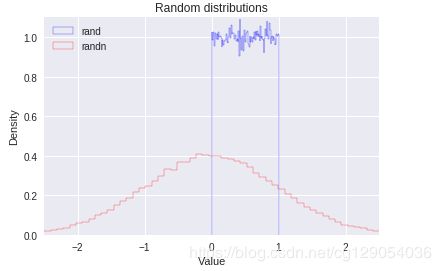
[-1.2885052 , -0.96175548, 0.24121048, 1.36009648]])为了更好的说明上面的随机分布,我们绘制以下图形:
%matplotlib inline
import matplotlib.pyplot as plt
plt.hist(np.random.rand(100000), normed=True, bins=100, histtype="step", color="blue", label="rand")
plt.hist(np.random.randn(100000), normed=True, bins=100, histtype="step", color="red", label="randn")
plt.axis([-2.5, 2.5, 0, 1.1])
plt.legend(loc = "upper left")
plt.title("Random distributions")
plt.xlabel("Value")
plt.ylabel("Density")
plt.show()你也可以通过函数来初始化数组:
def my_function(z, y, x):
return x * y + z
np.fromfunction(my_function, (3, 2, 10))
#输出
array([[[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.]],
[[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]],
[[ 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.],
[ 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.]]])2.Array data
NumPy的ndarray是很有效的,因为它们的所有元素必须具有相同的类型(通常是数字)。 您可以通过查看dtype属性来检查数据类型:
c = np.arange(1, 5)
print(c.dtype, c) #输出 " int64 [1 2 3 4]"
c = np.arange(1.0, 5.0)
print(c.dtype, c) #输出 " float64 [1. 2. 3. 4.]"
#创建数组时指定元素类型(复数)
d = np.arange(1, 5, dtype=np.complex64)
print(d.dtype, d) #输出 " complex64 [1.+0.j 2.+0.j 3.+0.j 4.+0.j]"
查看这篇文档了解所有的元素类型。
#itemsize属性返回每个项的大小(以字节为单位):
e = np.arange(1, 5, dtype=np.complex64)
e.itemsize #输出 "8"
#查看数组的存储地址
f = np.array([[1,2],[1000, 2000]], dtype=np.int32)
f.data
#输出
3.Reshaping an array
更改ndarray的形状就像设置其shape属性一样简单。 但是,阵列的大小必须保持不变。
g = np.arange(24)
print(g)
print("Rank:", g.ndim)
#输出
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Rank: 1
g.shape = (6, 4)
print(g)
print("Rank:", g.ndim)
#输出
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
Rank: 2
g.shape = (2, 3, 4)
print(g)
print("Rank:", g.ndim)
#输出
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
Rank: 3
1)reshape and ravel
reshape函数返回指向相同数据的新ndarray对象。 这意味着修改一个数组也会修改另一个数组。
g2 = g.reshape(4,6)
print(g2)
print("Rank:", g2.ndim)
#输出
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
Rank: 2
#修改矩阵g2中的元素
g2[1, 2] = 999
g2
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 999, 9, 10, 11],
[ 12, 13, 14, 15, 16, 17],
[ 18, 19, 20, 21, 22, 23]])
g
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[999, 9, 10, 11]],
[[ 12, 13, 14, 15],
[ 16, 17, 18, 19],
[ 20, 21, 22, 23]]])
#最后,ravel函数返回一个新的一维ndarray,它也指向相同的数据:
g.ravel()
array([ 0, 1, 2, 3, 4, 5, 6, 7, 999, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])4.Arithmetic operations
下面介绍关于ndarrays数组的几何运算:
a = np.array([14, 23, 32, 41])
b = np.array([5, 4, 3, 2])
print("a + b =", a + b)
print("a - b =", a - b)
print("a * b =", a * b)
print("a / b =", a / b)
print("a // b =", a // b)
print("a % b =", a % b)
print("a ** b =", a ** b)
#输出
a + b = [19 27 35 43]
a - b = [ 9 19 29 39]
a * b = [70 92 96 82]
a / b = [ 2.8 5.75 10.66666667 20.5 ]
a // b = [ 2 5 10 20]
a % b = [4 3 2 1]
a ** b = [537824 279841 32768 1681]注意,这里的乘法不是线性代数里的矩阵乘法。 我们将在下面讨论矩阵运算。阵列必须具有相同的形状。 如果他们形状不一样,NumPy将应用广播规则。
5.Broadcasting
通常,当NumPy期望操作的数组形状相同时但发现情况并非如此时,它会应用所谓的广播规则.
1)广播规则
#3维数组+1维数组
h = np.arange(5).reshape(1, 1, 5)
h
array([[[0, 1, 2, 3, 4]]])
#现在加上一维数组
h + [10, 20, 30, 40, 50] # same as: h + [[[10, 20, 30, 40, 50]]]
array([[[10, 21, 32, 43, 54]]])
#不同形状的2维数组相加
k = np.arange(6).reshape(2, 3)
k
array([[0, 1, 2],
[3, 4, 5]])
k + [[100], [200]] # same as: k + [[100, 100, 100], [200, 200, 200]]
array([[100, 101, 102],
[203, 204, 205]])
#我们还可以进行如下操作
k + [100, 200, 300] # after rule 1: [[100, 200, 300]], and after rule 2: [[100, 200, 300], [100, 200, 300]]
array([[100, 201, 302],
[103, 204, 305]])
k + 1000 # same as: k + [[1000, 1000, 1000], [1000, 1000, 1000]]
array([[1000, 1001, 1002],
[1003, 1004, 1005]])
#数组的size必须匹配,下面是不匹配的例子
try:
k + [33, 44]
except ValueError as e:
print(e)
operands could not be broadcast together with shapes (2,3) (2,) 下面来看一个不同类型的数组广播的例子
k1 = np.arange(0, 5, dtype=np.uint8)
print(k1.dtype, k1)
uint8 [0 1 2 3 4]
k3 = k1 + 1.5
print(k3.dtype, k3)
float64 [1.5 2.5 3.5 4.5 5.5]6.Conditional operators
下面看几个条件运算符在数组中应用的例子:
m = np.array([20, -5, 30, 40])
m < [15, 16, 35, 36]
array([False, True, True, False])
m < 25 # equivalent to m < [25, 25, 25, 25]
array([ True, True, False, False])
#这与布尔索引一起使用时最有用
m[m < 25]
array([20, -5])7.Mathematical and statistical functions
在numpy数组中有许多关于统计学的函数。
1)ndarray methods
#计算数组平均数
a = np.array([[-2.5, 3.1, 7], [10, 11, 12]])
print(a)
print("mean =", a.mean())
#输出
[[-2.5 3.1 7. ]
[10. 11. 12. ]]
mean = 6.766666666666667
#实用函数
for func in (a.min, a.max, a.sum, a.prod, a.std, a.var):
print(func.__name__, "=", func())
#输出
min = -2.5
max = 12.0
sum = 40.6
prod = -71610.0
std = 5.084835843520964
var = 25.855555555555554
#下面的函数接受一个可选的参数轴,该轴允许您请求对给定轴上的元素执行操作
c=np.arange(24).reshape(2,3,4)
c
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
c.sum(axis=0) # sum across matrices
array([[12, 14, 16, 18],
[20, 22, 24, 26],
[28, 30, 32, 34]])
c.sum(axis=1) # 安列求和
array([[12, 15, 18, 21],
[48, 51, 54, 57]])
c.sum(axis=(0,2)) # sum across matrices and columns
array([ 60, 92, 124])
2)Universal functions
NumPy还提供称为通用函数或ufunc的快速元素函数。 它们是简单函数的矢量化包装器。 例如,square返回一个新的ndarray,它是原始ndarray的副本,除了每个元素都是平方的。
a = np.array([[-2.5, 3.1, 7], [10, 11, 12]])
np.square(a)
array([[ 6.25, 9.61, 49. ],
[100. , 121. , 144. ]])
print("Original ndarray")
print(a)
for func in (np.abs, np.sqrt, np.exp, np.log, np.sign, np.ceil, np.modf, np.isnan, np.cos):
print("\n", func.__name__)
print(func(a))
Original ndarray
[[-2.5 3.1 7. ]
[10. 11. 12. ]]
absolute
[[ 2.5 3.1 7. ]
[10. 11. 12. ]]
sqrt
[[ nan 1.76068169 2.64575131]
[3.16227766 3.31662479 3.46410162]]
exp
[[8.20849986e-02 2.21979513e+01 1.09663316e+03]
[2.20264658e+04 5.98741417e+04 1.62754791e+05]]
log
[[ nan 1.13140211 1.94591015]
[2.30258509 2.39789527 2.48490665]]
sign
[[-1. 1. 1.]
[ 1. 1. 1.]]
ceil
[[-2. 4. 7.]
[10. 11. 12.]]
modf
(array([[-0.5, 0.1, 0. ],
[ 0. , 0. , 0. ]]), array([[-2., 3., 7.],
[10., 11., 12.]]))
isnan
[[False False False]
[False False False]]
cos
[[-0.80114362 -0.99913515 0.75390225]
[-0.83907153 0.0044257 0.84385396]]3)Binary ufuncs
a = np.array([1, -2, 3, 4])
b = np.array([2, 8, -1, 7])
np.add(a, b) # equivalent to a + b
array([ 3, 6, 2, 11])
np.greater(a, b) # equivalent to a > b
array([False, False, True, False])
np.maximum(a, b)
array([2, 8, 3, 7])
np.copysign(a, b)
array([ 1., 2., -3., 4.])
8.Array indexing
1维numpy数组可以像常规的python数组那样来访问。
a = np.array([1, 5, 3, 19, 13, 7, 3])
a[3] #输出 “19”
a[2:5] #输出 “array([ 3, 19, 13])”
a[2:-1] #输出 “array([ 3, 19, 13, 7])”
a[:2] #输出 “array([1, 5])”
#修改元素值
a[3]=999
a #输出 “array([ 1, 5, 3, 999, 13, 7, 3])”
#修改ndarray切片
a[2:5] = [997, 998, 999]
a #输出 “array([ 1, 5, 997, 998, 999, 7, 3])”1)Differences with regular python arrays
与常规python数组相反,如果您将单个值分配给ndarray切片,则会将其复制到整个切片中,这要归功于上面讨论的广播规则。
a[2:5] = -1
a #输出 "array([ 1, 5, -1, -1, -1, 7, 3])"
#创建切片并对其进行修改,实际上也将修改原始的ndarray.
a_slice = a[2:6]
a_slice[1] = 1000
a #输出 "array([ 1, 5, -1, 1000, -1, 7, 3])"
#同样地,修改原始数组元素,切片中的元素也会修改
a[3] = 2000
a_slice #输出 "array([ -1, 2000, -1, 7])"
#使用copy()函数来复制数据
another_slice = a[2:6].copy()
another_slice[1] = 3000
a #输出 "array([ 1, 5, -1, 2000, -1, 7, 3])"
2)Multi-dimensional arrays
通过为每个轴提供索引或切片,以逗号分隔,可以以类似的方式访问多维数组。
b = np.arange(48).reshape(4, 12)
b
#输出
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]])
b[1, 2] #输出 "14"
#输出第2行所有元素
b[1, :] #输出 "array([12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])"
#输出第1列所有元素
b[:, 1] #输出 "array([ 1, 13, 25, 37])"
#注意下面两个两个表达式的区别
b[1, :] #输出 "array([12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])"
b[1:2, :] #输出 "array([[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]])"3) Fancy indexing &Higher dimensions&Boolean indexing
我们的索引也可以是列表形式来访问多维数组
#切片前两行,2-4列的元素
b[(0,2), 2:5]
#输出
array([[ 2, 3, 4],
[26, 27, 28]])
b[:, (-1, 2, -1)]
#输出
array([[11, 2, 11],
[23, 14, 23],
[35, 26, 35],
[47, 38, 47]])
#返回一维数组
b[(-1, 2, -1, 2), (5, 9, 1, 9)] #输出“array([41, 33, 37, 33])”
#构建高维数组
c = b.reshape(4,2,6)
c
#输出
array([[[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]],
[[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]],
[[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]],
[[36, 37, 38, 39, 40, 41],
[42, 43, 44, 45, 46, 47]]])
c[2, 1, 4] #输出 "34"
c[2, :, 3] #输出 "array([27, 33])"
#如果省略某些轴的坐标,则返回这些轴中的所有元素
c[2, 1] #输出 "array([30, 31, 32, 33, 34, 35])"
#省略号的使用
c[2, ...] #c[2:, :, :]
#输出
array([[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]])
c[2, 1, ...] #c[2, 1, :]
#输出
array([30, 31, 32, 33, 34, 35])
c[2, ..., 3] #c[2, :, 3] array([27, 33])
c[..., 3] #c[:, :, 3]
#输出
array([[ 3, 9],
[15, 21],
[27, 33],
[39, 45]])
#布尔索引
b = np.arange(48).reshape(4, 12)
b
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]])
rows_on = np.array([True, False, True, False])
b[rows_on, :] #b[(0, 2), :]
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35]])
cols_on = np.array([False, True, False] * 4)
b[:, cols_on]
array([[ 1, 4, 7, 10],
[13, 16, 19, 22],
[25, 28, 31, 34],
[37, 40, 43, 46]])
#ix_函数使用
b[np.ix_(rows_on, cols_on)]
array([[ 1, 4, 7, 10],
[25, 28, 31, 34]])
np.ix_(rows_on, cols_on)
(array([[0],
[2]]), array([[ 1, 4, 7, 10]]))
b[b % 3 == 1]
array([ 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46])
9.Iterating
bn遍历arrays非常类似于遍历常规python数组。 但是完成的是对多维数组的遍历。
#生成一个三维数组
c = np.arange(24).reshape(2, 3, 4)
c
#输出
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
for m in c:
print("Item:")
print(m)
#输出
Item:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
Item:
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
#len(c) == c.shape[0]
for i in range(len(c)):
print("Item:")
print(c[i])
#输出
Item:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
Item:
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
#通过flat属性遍历所有元素
for i in c.flat:
print("Item:", i)
Item: 0
Item: 1
Item: 2
Item: 3
Item: 4
Item: 5
Item: 6
Item: 7
Item: 8
Item: 9
Item: 10
Item: 11
Item: 12
Item: 13
Item: 14
Item: 15
Item: 16
Item: 17
Item: 18
Item: 19
Item: 20
Item: 21
Item: 22
Item: 2310.Stacking arrays
将不同的数组堆叠在一起通常很有用。 NumPy提供了几种功能来实现这一目标。 让我们从创建一些数组开始。
#创建数组q1,q2,q3
q1 = np.full((3,4), 1.0)
q1
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
q2 = np.full((4,4), 2.0)
q2
array([[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.]])
q3 = np.full((3,4), 3.0)
q3
array([[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]])1)vstack
现在使用vstack函数来堆叠数组:
q4 = np.vstack((q1, q2, q3))
q4
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]])
q4.shape
(10, 4)2)hstack
同样,我们也可以在水平方向上堆叠数组:
q5 = np.hstack((q1, q3))
q5
array([[1., 1., 1., 1., 3., 3., 3., 3.],
[1., 1., 1., 1., 3., 3., 3., 3.],
[1., 1., 1., 1., 3., 3., 3., 3.]])
q5.shape
(3, 8)3)concatenate
concatenate函数沿任何给定的现有轴堆栈数组。
q7 = np.concatenate((q1, q2, q3), axis=0) # axis=0 == vstack
q7
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]])
q7.shape
(10, 4)4)stack
stack函数沿新轴堆叠数组。 所有阵列必须具有相同的形状。
q8 = np.stack((q1, q3))
q8
array([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[3., 3., 3., 3.],
[3., 3., 3., 3.],
[3., 3., 3., 3.]]])
q8.shape
(2, 3, 4)11.Splitting arrays
分裂与堆叠相反。 例如,让我们使用vsplit函数垂直分割矩阵。首先让我们创建一个6x4矩阵:
r = np.arange(24).reshape(6,4)
r
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
#现在开始把数组平分三份
r1, r2, r3 = np.vsplit(r, 3)
r1
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
r3
array([[16, 17, 18, 19],
[20, 21, 22, 23]])
#水平方向平分数组
r4, r5 = np.hsplit(r, 2)
r4
array([[ 0, 1],
[ 4, 5],
[ 8, 9],
[12, 13],
[16, 17],
[20, 21]])
12.Transposing arrays
转置方法在ndarray的数据上创建一个新视图,以给定的顺序进行置换。例如,让我们创建一个3D数组:
t = np.arange(24).reshape(4,2,3)
t
array([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23]]])
#我们创建一个ndarray,使轴依次向左平移
t1 = t.transpose((1,2,0))
t1
array([[[ 0, 6, 12, 18],
[ 1, 7, 13, 19],
[ 2, 8, 14, 20]],
[[ 3, 9, 15, 21],
[ 4, 10, 16, 22],
[ 5, 11, 17, 23]]])
t1.shape
(2, 3, 4)
#默认情况下,转置会反转维度的顺序:
t2 = t.transpose()
t2
array([[[ 0, 6, 12, 18],
[ 3, 9, 15, 21]],
[[ 1, 7, 13, 19],
[ 4, 10, 16, 22]],
[[ 2, 8, 14, 20],
[ 5, 11, 17, 23]]])
t2.shape
(3, 2, 4)
#NumPy提供便捷功能交换轴来交换两个轴
t3 = t.swapaxes(0,1)
t3
array([[[ 0, 1, 2],
[ 6, 7, 8],
[12, 13, 14],
[18, 19, 20]],
[[ 3, 4, 5],
[ 9, 10, 11],
[15, 16, 17],
[21, 22, 23]]])
t3.shape
(2, 4, 3)13.Vectorization
Numpy最有用的是向量化。 这可以让我避免显示使用for循环。来看下面这个例子:
import math
data = np.empty((768, 1024))
for y in range(768):
for x in range(1024):
data[y, x] = math.sin(x*y/40.5) # 非常低效
#我们向量化创建数组
x_coords = np.arange(0, 1024) # [0, 1, 2, ..., 1023]
y_coords = np.arange(0, 768) # [0, 1, 2, ..., 767]
X, Y = np.meshgrid(x_coords, y_coords)
X
array([[ 0, 1, 2, ..., 1021, 1022, 1023],
[ 0, 1, 2, ..., 1021, 1022, 1023],
[ 0, 1, 2, ..., 1021, 1022, 1023],
...,
[ 0, 1, 2, ..., 1021, 1022, 1023],
[ 0, 1, 2, ..., 1021, 1022, 1023],
[ 0, 1, 2, ..., 1021, 1022, 1023]])
Y
array([[ 0, 0, 0, ..., 0, 0, 0],
[ 1, 1, 1, ..., 1, 1, 1],
[ 2, 2, 2, ..., 2, 2, 2],
...,
[765, 765, 765, ..., 765, 765, 765],
[766, 766, 766, ..., 766, 766, 766],
[767, 767, 767, ..., 767, 767, 767]])
#X和Y都是768x1024维数组,现在我们进行数组运算
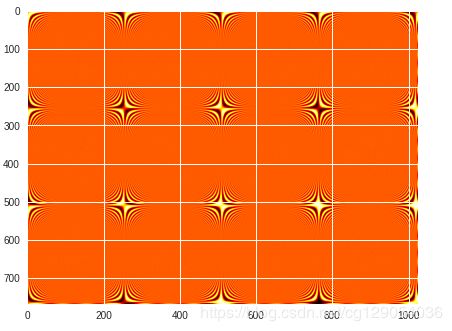
data = np.sin(X*Y/40.5)
#显示图形
import matplotlib.pyplot as plt
import matplotlib.cm as cm
fig = plt.figure(1, figsize=(7, 6))
plt.imshow(data, cmap=cm.hot, interpolation="bicubic")
plt.show()
14.Saving and loading
Numpy提供了很多方式保存数组:
#创建一个随机数组,然后保存
a = np.random.rand(2,3)
a
array([[0.13173958, 0.18005176, 0.26791744],
[0.74531068, 0.07925457, 0.02683962]])
#自动保存为.npy格式
np.save("my_array", a)
#打开刚刚保存的数组文件
with open("my_array.npy", "rb") as f:
content = f.read()
content
a_loaded = np.load("my_array.npy")
a_loaded
array([[0.13173958, 0.18005176, 0.26791744],
[0.74531068, 0.07925457, 0.02683962]])
#Text format
np.savetxt("my_array.csv", a)
with open("my_array.csv", "rt") as f:
print(f.read())
1.317395793717837105e-01 1.800517644099779435e-01 2.679174359928241378e-01
7.453106759162891892e-01 7.925457061278873283e-02 2.683962400554706917e-02
#设置逗号分隔符
np.savetxt("my_array.csv", a, delimiter=",")
a_loaded = np.loadtxt("my_array.csv", delimiter=",")
a_loaded
array([[0.13173958, 0.18005176, 0.26791744],
[0.74531068, 0.07925457, 0.02683962]])
#Zipped .npz format
b = np.arange(24, dtype=np.uint8).reshape(2, 3, 4)
b
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]], dtype=uint8)
np.savez("my_arrays", my_a=a, my_b=b)
with open("my_arrays.npz", "rb") as f:
content = f.read()
repr(content)[:180] + "[...]"
#加载文件
my_arrays = np.load("my_arrays.npz")
my_arrays
my_arrays.keys()
['my_b', 'my_a']
my_arrays["my_a"]
array([[0.13173958, 0.18005176, 0.26791744],
[0.74531068, 0.07925457, 0.02683962]])综上,我们已经学完了Numpy的基本使用,在下一篇文章中将介绍如何使用Numpy进行线性代数运算。