java实现二叉查找树(插入、删除、遍历、查找)
闲话:
继续撸数据结构和算法。看数据结构推荐一个可视化工具吧(http://visualgo.net/),没有图凭脑袋想是很痛苦的。
正文:
二叉查找树,也叫二叉搜索树、有序二叉树,排序二叉树,满足以下性质(非严谨描述):
1.对于每个节点,其左子节点要么为空,要么值小于该节点值。
2.对于每个节点,其右子节点要么为空,要么值大于该节点值。
3.没有键值相等的点。
通俗的归纳一下性质,二叉查找树中每个节点的值都大于其左子节点,小于其右子节点(如果左右子节点存在的话)。所以二叉查找树中每个节点的左边,整棵左树都是小于它的节点;右边,整棵右树都是大于它的节点。
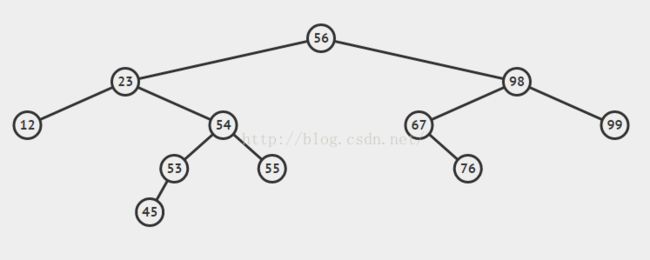
例图:
基于这样的特性,查找的时候就很好操作了,从根节点开始,查找,如果值大于节点值,往右找;如果值小于节点值,往左找;如果值刚好相等,就找到了。是不是看着就能写出代码了?这种查找过程很像二分查找法,但是那个是数组结构,这个是树结构。
二叉查找树的操作基本概括为:插入值,删除值,查找值以及二叉树的遍历。
这里面,删除是最麻烦的。
(本来觉得写数据结构还是用c语言最好的,直接可以操作指针,清晰明了效率高,但是c确实丢了太久了,而且现在主要目的是温习数据结构和算法的知识,所以只能放弃用c的想法,以后如果需要再学习,先用最熟悉的java来实现代码)
下面来看具体的操作和逻辑,附带贴上代码。
首先是准备工作,java写,没指针,只有利用引用了,节点类是少不了的:
/**
* 节点
*
* @author zhangyu
*
* @param
*/
public class Node {
// 节点数据
T data;
// 父节点,左右子节点
Node fatherNode, leftChildNode, rightChildNode;
//是否是左节点、是否是右节点
boolean isLeftChild = false, isRightChild = false;
//左节点是否存在
public boolean haveLeftChild() {
return !(leftChildNode == null);
}
//右节点是否存在
public boolean haveRightChild() {
return !(rightChildNode == null);
}
//构造方法
public Node(boolean isLeft, boolean isRight) {
isLeftChild = isLeft;
isRightChild = isRight;
}
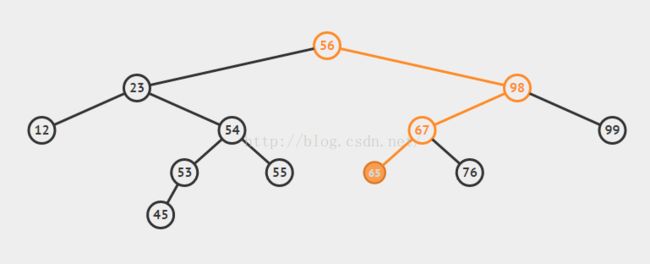
} 例图(插入65,黄色线为比较的轨迹):
代码:
/**
* 插入节点
*
* @param insertData 待插入的数据
* @param node 开始比较的节点
*/
private void insertNode(T insertData, Node node) {
int compareResult = insertData.compareTo(node.data);
if (compareResult == 0)// 相等
return;
else if (compareResult > 0) {// 大于节点值
if (node.rightChildNode == null) {
node.rightChildNode = new Node(false, true);
node.rightChildNode.data = insertData;// 插入值
node.rightChildNode.fatherNode = node;
return;
} else
insertNode(insertData, node.rightChildNode);// 继续对比右子节点
} else {// 小于节点值
if (node.leftChildNode == null) {
node.leftChildNode = new Node(true, false);
node.leftChildNode.data = insertData;// 插入值
node.leftChildNode.fatherNode = node;
return;
} else
insertNode(insertData, node.leftChildNode);// 继续对比左子节点
}
}
/**
* 插入节点
*
* @param insertData 待插入的数据
*/
public void insertNode(T insertData) {
if (treeRoot.data == null) {
treeRoot.data = insertData;
return;
}
insertNode(insertData, treeRoot);
}
/**
* 从某个节点开始搜索
*
* @param target 目标值
* @param startSearchNode 开始搜索的节点
* @return
*/
public Node searchNode(T target, Node startNode) {
int compareResult = target.compareTo(startNode.data);
if (compareResult == 0)
return startNode;
else if (compareResult > 0 && startNode.rightChildNode != null)
return searchNode(target, startNode.rightChildNode);
else if (compareResult < 0 && startNode.leftChildNode != null)
return searchNode(target, startNode.leftChildNode);
else
return null;
}
/**
* 查找数据所在节点
*
* @param target 目标数据
* @return null或数据所在节点
*/
public Node searchNode(T target) {
if (treeRoot.data == null)
return null;
return searchNode(target, treeRoot);
}
/**
* 查找数据
* @param target 目标数据(有部分检索需要的信息即可)
* @return 完整目标数据
*/
public BaseData searchData(T target) {
Node node = searchNode(target);
if (node != null)
return node.data;
return null;
}然后看删除操作,这个删除真的是有点麻烦,为了把这部分理清楚,把代码调通,几乎花费了一整天的时间,慢慢捋来~
删除分为以下几种情况:
1.被删除的节点只有左节点或者只有右节点,这种情况好办,因为节点在一条链上,没有分叉,就像处理链表一样把这个节点摘掉就行了。让它的父节点关联它的子节点,它的子节点关联它的父节点就完事。如果它没有父节点,说明它是根节点,直接将其子节点作为根节点就行。
2.被删除的节点没有子节点,这种情况也很简单,它是叶子节点,直接置空,将其父节点对应的子节点也置空,就完事。
3.被删除的节点有左右子节点。这种情况就有点麻烦了。
这里需要了解两个概念,叫“前驱”和“后继”。分别是树中小于它的最大值和大于它的最小值,如果把树结构中的所有节点按顺序拍好的话,它的前驱和它的后继两个节点刚好在它左右紧挨着它。当一个节点被删除时,为了保证二叉树的结构不被破坏,要让它的前驱或者后继节点来代替它的位置,然后将它的前驱或者后继节点同样做删除操作。
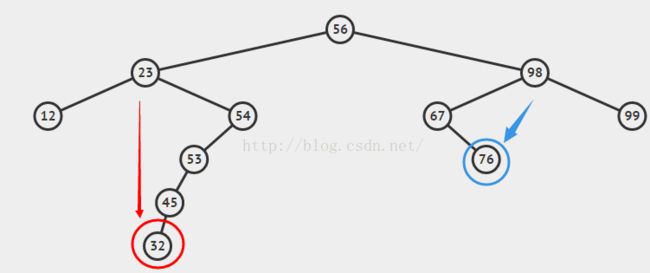
那么怎样找前驱或者后继呢。小于它的最大值,就是在树中在它左边最靠右的那个节点。同样,大于它的最小值,就是在树中在它右边最靠左的那个节点。当一个节点既有左子节点又有右子节点时,前驱就是它的左子节点的右子节点的右子节点...直到最右子节点;后继就是它的右子节点的左子节点的左子节点...直到最左子节点。上个图吧:
23的后继是32;98的前驱是76。
上图中,当23被删除,则可以用32代替它,也可以用12代替它,然后删除掉32(或者12)的原节点就行了;同理,当98被删除时,可以用76代替它,或者用99代替它,然后删除76(或者99)的原节点就行了。当然,如果被删除节点是根节点,就用代替它的节点作为根节点然后删除代替节点的原节点就行了。再次推荐你用可视化工具http://zh.visualgo.net/bst来看二叉树的各种操作动画,简单明了。
所以删除操作代码如下(代码用的是后继节点替代待删除节点):
/**
* 删除节点
*
* @param node 待删除节点
*/
private void deleteNode(Node node) {
// 如果按顺序排列好节点,它的前驱和后继就是这个序列上紧挨着它左右两侧的节点.
// 如果节点只有左节点或者只有右节点
if (node.haveLeftChild() && !node.haveRightChild()) {// 只有左节点
if (node.isLeftChild) {
node.fatherNode.leftChildNode = node.leftChildNode;
} else if (node.isRightChild) {
node.fatherNode.rightChildNode = node.leftChildNode;
} else// 待删除节点是根节点
treeRoot = node.leftChildNode;
node.leftChildNode.fatherNode = node.fatherNode;
} else if (node.haveRightChild() && !node.haveLeftChild()) {// 只有右节点
if (node.isLeftChild) {
node.fatherNode.leftChildNode = node.rightChildNode;
} else if (node.isRightChild) {
node.fatherNode.rightChildNode = node.rightChildNode;
} else// 待删除节点是根节点
treeRoot = node.rightChildNode;
node.rightChildNode.fatherNode = node.fatherNode;
} else if (node.haveLeftChild() && node.haveRightChild()) {// 有左右子节点
Node successorNode = getSuccessorNode(node);
if (successorNode == node.rightChildNode) {// 后继节点是右子节点
successorNode.fatherNode = node.fatherNode;
if (node.isLeftChild)
node.fatherNode.leftChildNode = successorNode;
else if (node.isRightChild)
node.fatherNode.rightChildNode = successorNode;
else {// 是根节点
successorNode = treeRoot;
}
successorNode.fatherNode = node.fatherNode;
successorNode.leftChildNode = node.leftChildNode;
node.leftChildNode.fatherNode = successorNode;
} else {// 后继节点是右子节点的最左子节点
if (successorNode.haveRightChild()) {// 左子节点有右子树
successorNode.fatherNode.leftChildNode = successorNode.rightChildNode;
successorNode.rightChildNode.fatherNode = successorNode.fatherNode;
replaceNode(node, successorNode);
} else {// 左子节点没有右子树
// 叶节点,直接删除
successorNode.fatherNode.leftChildNode = null;
replaceNode(node, successorNode);
}
}
} else {// 没有子节点
if (node.isLeftChild) {
node.fatherNode.leftChildNode = null;
} else if (node.isRightChild) {
node.fatherNode.rightChildNode = null;
}
}
node = null;
}
/**
* 非相邻节点的替换逻辑(非相邻加粗!)
* @param node 被替换节点
* @param replaceNode 替换的节点
*/
private void replaceNode(Node node, Node replaceNode) {
if (node.isLeftChild)
node.fatherNode.leftChildNode = replaceNode;
else if (node.isRightChild)
node.fatherNode.rightChildNode = replaceNode;
else {// node是根节点
treeRoot = replaceNode;
}
node.leftChildNode.fatherNode = node.rightChildNode.fatherNode = replaceNode;
replaceNode.leftChildNode = node.leftChildNode;
replaceNode.rightChildNode = node.rightChildNode;
}
/**
* 获取一个节点的后继节点
* @param node
* @return
*/
private Node getSuccessorNode(Node node) {
if (!node.haveRightChild()) {// 没有右子树
return null;
}
Node targetNode = node.rightChildNode;
while (targetNode.haveLeftChild()) {// 找右子树的最左孩子,保证返回的节点一定没有左子树
targetNode = targetNode.leftChildNode;
}
return targetNode;
}
/**
* 删除数中的数据
* @param baseData
*/
public void deleteData(T baseData) {
Node node = searchNode(baseData);
deleteNode(node);
}
/**
* 遍历节点
* @param node
*/
private void preOrder(Node node) {
System.out.println("" + node.data.toString());
if (node.haveLeftChild())
preOrder(node.leftChildNode);
if (node.haveRightChild())
preOrder(node.rightChildNode);
}
/**
* 遍历树(前序遍历)
*/
public void preOrder() {
if (treeRoot == null)
return;
preOrder(treeRoot);
}